SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. isakharov
15% годовых – это много или мало?
- 11 декабря 2012, 15:53
- |
Давно чесались руки написать про сложный процент, но не мог найти подходящий пример, который бы позволил раскрыть красоту этого простого инструмента. И вот свершилось!
Ко всему прочему вижу отчаяние многих мелких инвесторов, не чувствующих прибыли от своих инвестиций и потому безрассудно рискующих на рынке. А всего-то нужно посмотреть на инвестиции в долгосрочной перспективе.
И да, далее много буков, знаки умножения и возведения в степень. Придется вспомнить математику 7го класса.
Сложный процент
Предположим, что мы положили на счет сумму, равную 1000 руб., под 8% годовых. Сколько средств будет у нас через 3 года в начале 4го периода?
Для наглядности нарисуем временной горизонт инвестирования:
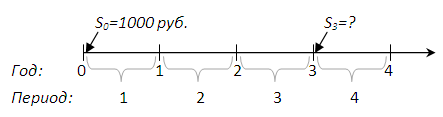
Обозначим годовой процент буквой R от английского слова(rate). Инвестиция – это как рождение ребенка. Первый день рождения нашей инвестиции
S0

В начале 4-го периода у нас на счету будет сумма, приблизительно равная 1260 рублям, которую можно рассчитать по формуле:
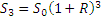
Формула расчета стоимости активов (например, денег, акций, недвижимости) с учетом процента за n лет не сильно отличается от формулы расчета стоимости активов с учетом процента за 3 года:
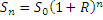
Во всем мире будущую стоимость актива (Sn), принято обозначать буквами FV (Future Value), а текущую стоимость актива (S0) обозначают буквами PV (Present Value). Теперь предыдущая формула приобретает следующий вид:
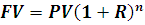
Зная процент и будущую стоимость актива через n лет, мы легко можем рассчитать его текущую стоимость:
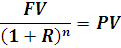
Эта формула может пригодиться, если потребуется рассчитать, какое количество денег необходимо инвестировать сейчас под заданный процент, чтобы получить определенную сумму в будущем.
В 1626 году ирокезы продали голландским колонистам остров Манхэттен за 60 гульденов. В то время 60 голландских гульденов можно было обменять на 18 Троицких унций серебра. Позднее, когда появились баксы, одну унцию можно было продать за 4 доллара. Таким образом, остров Манхэттэн был продан за 72 доллара США. Давайте представим, что индейцы положили эти деньги в банк под 6% годовых в начале 1627 года. Какая сумма была бы у них на счету в начале 2013 года?
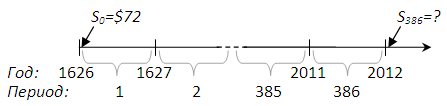
Стоит отметить, что новый год празднуется в момент начала этого года, а не в момент конца. Другими словами, то, что у нас на временной шкале отмечено цифрой 2012 – это праздник Нового Года 2013, года Змеи по китайскому календарю.
Проведем небольшие расчеты:
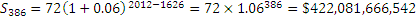
Наши индейцы имели бы новогодний подарок в виде депозита размером в422 миллиарда долларов США! Для сравнения, Московский Кремль, по оценкам аналитиков в сфере недвижимости, стоит «всего» $50 млд. Разомнитесь и посчитайте потенциальный депозит индейцев при 7% годовых.
Но давайте двигаться дальше. Что произойдет, если мы каждый год будем пополнять наш инвестиционный счет и через 3 года заглянем в него?
Все очень просто. Каждая новая инвестиция будет иметь свой собственный временной горизонт. Наша первоначальная инвестиция S0 пройдет путь в три года и получит свои проценты за этот период. Следующая инвестиция S1 пройдет путь в два года. Третья инвестиция S2 пройдет путь в один год. А четвертая инвестиция S3 ляжет на счет, но мы не успеем получить по ней процентный доход.
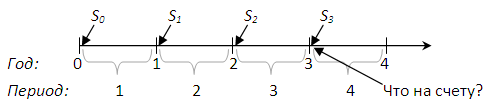
Сведем все в таблицу:

Сложим будущую стоимость всех инвестиций и получим будущую суммарную стоимость активов через 3 года или, другими словами, все деньги, которые накопятся у нас на счету.
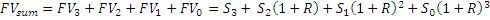
Мы рассчитали FVsum за 4 периода.
Упростим ситуацию. Предположим, что размер инвестиций всегда одинаков. Обозначим равные инвестиции переменной PMT (англ., payment).
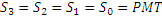
Тогда будущая сумма накоплений FVsum за n периодов с учетом процента будет равна:
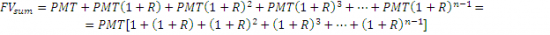
Перед нами геометрическая прогрессия. Надеюсь, пока все более-менее понятно. Добавим немного магии. Чтобы не таскать за собой выражение (1+R) представим его в виде символа q и умножим все на (q-1)/(q-1) Затем оптимизируем формулу, сократим то, что можно сократить, и обратно заменим q на (1+R):
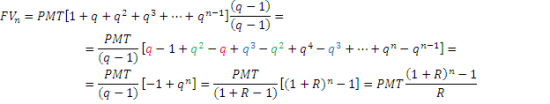
Итак, будущая стоимость активов через n лет с ежегодными равными инвестициями будет равна:
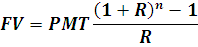
Мы получили формулу сложного процента с учетом ежегодных инвестиций и можем ее легко использовать в жизни.
Текущая стоимость активов PV, с учетом ежегодных платежей PMT, выводится просто:
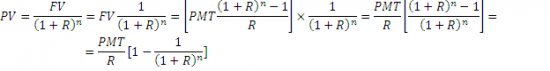
Итак,
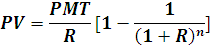
Для чего может использоваться эта формула? Ну, например, если у нас есть какое-то количество денег, мы можем ежегодно тратить определенную сумму, а на остаток иметь годовой процент. Данная формула позволит нам рассчитать текущее количество денег на счету (PV), которых нам хватит на n лет, если ежегодно мы будем тратить сумму PMT, с учетом годового процентаR.
Теперь мы знаем, что:
Вам 30, вы молоды, крепки и полны надежд. Вы планируете уйти на заслуженный отдых в 60 лет. Вы желаете тратить $100,000 в год в период с 60 до 80 лет. Если все будет удачно, вы проживете дольше, но смерть – одна из самых предсказуемых вещей на планете и статистика говорит, что 80 лет для обычного человека – это весьма неплохой результат. Вы понимаете, что в период с 50 до 60 лет вам будет сложно откладывать деньги, но вы будете продолжать работать, что позволит вам не съедать свой капитал. А вот с 30 до 50 лет вы можете себе позволить ежегодно откладывать какие-то деньги. Сколько и под какой процент вы можете откладывать ежегодно, чтобы в 60 лет иметь достойный бонус?
Нарисуем горизонты инвестирования:
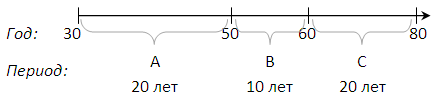
Начнем с конца и рассмотрим период С. Предположим, что наши рыночные инвестиции приносят ежегодно 15% годовых. Сколько денег у нас должно быть на счету в 60 лет, чтобы мы могли тратить до 80-и лет ежегодно по $100,000? Представим, что нам 60 лет прямо сейчас. Следовательно, нам нужно знать, сколько сейчас денег у нас на счету или, другими словами, текущую стоимость активов (PV), которые мы хотим потратить в ближайшие 20 лет, совершая ежегодные траты, равного размера:

Рассчитаем текущую стоимость активов, которых нам должно хватить на 20 лет:
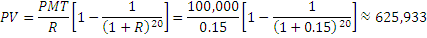
Мы выяснили, сколько денег должно быть на счету, когда нам стукнет 60. Теперь рассмотрим период B и найдем, сколько денег мы должны иметь в 50 лет, если в следующие 10 лет мы не сможем дополнительно инвестировать. Итак, нам 50 лет и нам известно, что в 60 лет у нас на счету должна образоваться сумма в $625,933. Мы смотрим на эти деньги, как на нашу будущую стоимость активов или FV (то, что в 60 лет для нас станет PV, в 50 лет будет еще только будущим, т.е. FV). Процент тот же. Период B длится 10 лет. Снова рассчитываем текущие активы, но с перспективы 50-летнего человека

Тогда применим формулу расчета PV без учета PMT:
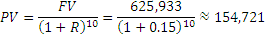
Итак, в 50 лет у нас на счету должна быть сумма, равная $154,721.
В завершение рассмотрим период А. В эти годы мы планируем активно инвестировать. Но сколько? Нам 30 лет и мы знаем нашу будущую стоимость активов FV, равную $154,721. Процент по-прежнему 15%. Период инвестиций — 20 лет.
Воспользуемся формулой:
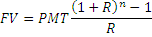
Перевернем ее так, чтобы рассчитать наши ежегодные инвестиции PMT:
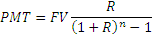
Определим начальные данные для периода А:
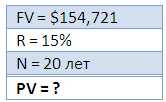
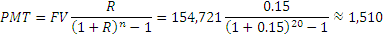
Вот и все. Инвестиции $1,510 в год в течение 20 лет, пока молоды, и траты $100,000 в год, когда уже мудры.
Остальные выводы вы можете сделать сами и определить для себя: 15% годовых – это много или мало. Готовы ли вы нести риски за дополнительные проценты. Сможете ли вы стать дисциплинированным инвестором или так и будете метаться в поисках Граалей.
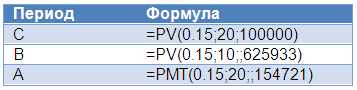
P.S. Excel и OpenOffice имеет все формулы для расчета PV, FV и PMT. Последний пример можно рассчитать в таблицах следующим образом:
Ко всему прочему вижу отчаяние многих мелких инвесторов, не чувствующих прибыли от своих инвестиций и потому безрассудно рискующих на рынке. А всего-то нужно посмотреть на инвестиции в долгосрочной перспективе.
И да, далее много буков, знаки умножения и возведения в степень. Придется вспомнить математику 7го класса.
Сложный процент
Предположим, что мы положили на счет сумму, равную 1000 руб., под 8% годовых. Сколько средств будет у нас через 3 года в начале 4го периода?
Для наглядности нарисуем временной горизонт инвестирования:

Обозначим годовой процент буквой R от английского слова(rate). Инвестиция – это как рождение ребенка. Первый день рождения нашей инвестиции
S0

В начале 4-го периода у нас на счету будет сумма, приблизительно равная 1260 рублям, которую можно рассчитать по формуле:
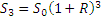
Формула расчета стоимости активов (например, денег, акций, недвижимости) с учетом процента за n лет не сильно отличается от формулы расчета стоимости активов с учетом процента за 3 года:
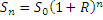
Во всем мире будущую стоимость актива (Sn), принято обозначать буквами FV (Future Value), а текущую стоимость актива (S0) обозначают буквами PV (Present Value). Теперь предыдущая формула приобретает следующий вид:
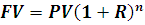
Зная процент и будущую стоимость актива через n лет, мы легко можем рассчитать его текущую стоимость:
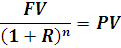
Эта формула может пригодиться, если потребуется рассчитать, какое количество денег необходимо инвестировать сейчас под заданный процент, чтобы получить определенную сумму в будущем.
В 1626 году ирокезы продали голландским колонистам остров Манхэттен за 60 гульденов. В то время 60 голландских гульденов можно было обменять на 18 Троицких унций серебра. Позднее, когда появились баксы, одну унцию можно было продать за 4 доллара. Таким образом, остров Манхэттэн был продан за 72 доллара США. Давайте представим, что индейцы положили эти деньги в банк под 6% годовых в начале 1627 года. Какая сумма была бы у них на счету в начале 2013 года?

Стоит отметить, что новый год празднуется в момент начала этого года, а не в момент конца. Другими словами, то, что у нас на временной шкале отмечено цифрой 2012 – это праздник Нового Года 2013, года Змеи по китайскому календарю.
Проведем небольшие расчеты:
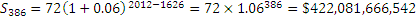
Наши индейцы имели бы новогодний подарок в виде депозита размером в422 миллиарда долларов США! Для сравнения, Московский Кремль, по оценкам аналитиков в сфере недвижимости, стоит «всего» $50 млд. Разомнитесь и посчитайте потенциальный депозит индейцев при 7% годовых.
Но давайте двигаться дальше. Что произойдет, если мы каждый год будем пополнять наш инвестиционный счет и через 3 года заглянем в него?
Все очень просто. Каждая новая инвестиция будет иметь свой собственный временной горизонт. Наша первоначальная инвестиция S0 пройдет путь в три года и получит свои проценты за этот период. Следующая инвестиция S1 пройдет путь в два года. Третья инвестиция S2 пройдет путь в один год. А четвертая инвестиция S3 ляжет на счет, но мы не успеем получить по ней процентный доход.

Сведем все в таблицу:

Сложим будущую стоимость всех инвестиций и получим будущую суммарную стоимость активов через 3 года или, другими словами, все деньги, которые накопятся у нас на счету.
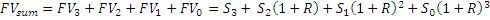
Мы рассчитали FVsum за 4 периода.
Упростим ситуацию. Предположим, что размер инвестиций всегда одинаков. Обозначим равные инвестиции переменной PMT (англ., payment).
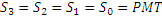
Тогда будущая сумма накоплений FVsum за n периодов с учетом процента будет равна:
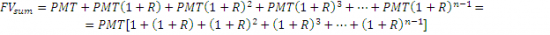
Перед нами геометрическая прогрессия. Надеюсь, пока все более-менее понятно. Добавим немного магии. Чтобы не таскать за собой выражение (1+R) представим его в виде символа q и умножим все на (q-1)/(q-1) Затем оптимизируем формулу, сократим то, что можно сократить, и обратно заменим q на (1+R):
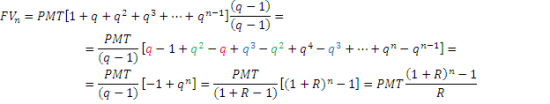
Итак, будущая стоимость активов через n лет с ежегодными равными инвестициями будет равна:
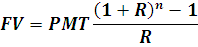
Мы получили формулу сложного процента с учетом ежегодных инвестиций и можем ее легко использовать в жизни.
Текущая стоимость активов PV, с учетом ежегодных платежей PMT, выводится просто:
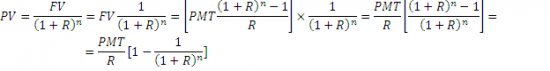
Итак,
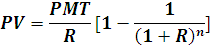
Для чего может использоваться эта формула? Ну, например, если у нас есть какое-то количество денег, мы можем ежегодно тратить определенную сумму, а на остаток иметь годовой процент. Данная формула позволит нам рассчитать текущее количество денег на счету (PV), которых нам хватит на n лет, если ежегодно мы будем тратить сумму PMT, с учетом годового процентаR.
Теперь мы знаем, что:
- FV– будущая стоимость активов,
- PV– текущая стоимость активов,
- PMT– ежегодный платеж (трата или инвестиция, смотря с какой стороны смотреть).
Вам 30, вы молоды, крепки и полны надежд. Вы планируете уйти на заслуженный отдых в 60 лет. Вы желаете тратить $100,000 в год в период с 60 до 80 лет. Если все будет удачно, вы проживете дольше, но смерть – одна из самых предсказуемых вещей на планете и статистика говорит, что 80 лет для обычного человека – это весьма неплохой результат. Вы понимаете, что в период с 50 до 60 лет вам будет сложно откладывать деньги, но вы будете продолжать работать, что позволит вам не съедать свой капитал. А вот с 30 до 50 лет вы можете себе позволить ежегодно откладывать какие-то деньги. Сколько и под какой процент вы можете откладывать ежегодно, чтобы в 60 лет иметь достойный бонус?
Нарисуем горизонты инвестирования:

Начнем с конца и рассмотрим период С. Предположим, что наши рыночные инвестиции приносят ежегодно 15% годовых. Сколько денег у нас должно быть на счету в 60 лет, чтобы мы могли тратить до 80-и лет ежегодно по $100,000? Представим, что нам 60 лет прямо сейчас. Следовательно, нам нужно знать, сколько сейчас денег у нас на счету или, другими словами, текущую стоимость активов (PV), которые мы хотим потратить в ближайшие 20 лет, совершая ежегодные траты, равного размера:

Рассчитаем текущую стоимость активов, которых нам должно хватить на 20 лет:
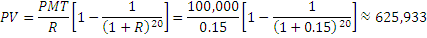
Мы выяснили, сколько денег должно быть на счету, когда нам стукнет 60. Теперь рассмотрим период B и найдем, сколько денег мы должны иметь в 50 лет, если в следующие 10 лет мы не сможем дополнительно инвестировать. Итак, нам 50 лет и нам известно, что в 60 лет у нас на счету должна образоваться сумма в $625,933. Мы смотрим на эти деньги, как на нашу будущую стоимость активов или FV (то, что в 60 лет для нас станет PV, в 50 лет будет еще только будущим, т.е. FV). Процент тот же. Период B длится 10 лет. Снова рассчитываем текущие активы, но с перспективы 50-летнего человека

Тогда применим формулу расчета PV без учета PMT:
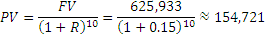
Итак, в 50 лет у нас на счету должна быть сумма, равная $154,721.
В завершение рассмотрим период А. В эти годы мы планируем активно инвестировать. Но сколько? Нам 30 лет и мы знаем нашу будущую стоимость активов FV, равную $154,721. Процент по-прежнему 15%. Период инвестиций — 20 лет.
Воспользуемся формулой:
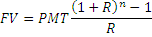
Перевернем ее так, чтобы рассчитать наши ежегодные инвестиции PMT:
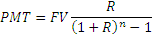
Определим начальные данные для периода А:
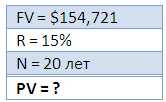
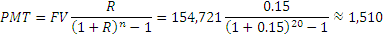
Вот и все. Инвестиции $1,510 в год в течение 20 лет, пока молоды, и траты $100,000 в год, когда уже мудры.
Остальные выводы вы можете сделать сами и определить для себя: 15% годовых – это много или мало. Готовы ли вы нести риски за дополнительные проценты. Сможете ли вы стать дисциплинированным инвестором или так и будете метаться в поисках Граалей.
P.S. Excel и OpenOffice имеет все формулы для расчета PV, FV и PMT. Последний пример можно рассчитать в таблицах следующим образом:




















Ему исполняется 79 и он все еще жив. Он снимает последнюю сотню, празднует день рождения и уезжает в Новую Зеландию с молодой и богатой женой.
как-будто никто не знает этих прописных
и ты еще инвесторам вот объясни это :-)
про 15 то годовых
в 61 год будет 625,933-100 000 долларов+ проценыт по оставшейся сумме.
Надо будет снимать каждый месяц 8333,333 доллара.
в 1 месяц 60 лет снимаем: -8333,33+625933= остаётся6175600
на 1 число сл месяца ему приходят 1,01125% проценты, т.к. 0,15/12+1. И сумма получается 1,01125%*6175600=625320
У меня получилось, что на начало 212 месяца(т.е. 77 лет) после выхода на пенсию у него останется 589 долларов, после того как он снимет 8333 доллара. Ему на оставшиеся 3 года не хватит.
Вы считали, что проценты приходят через год так? Скажем покупка облигаций с полугодовыми купонами, даст больше прибыли, если их реивестировать.
Надеюсь таблица поможет…
1 не факт что через 5 лет они дадут такой процент
2 не факт что через 5 лет они ваще будут
smart-lab.ru/blog/92400.php
10К есть?
15% — большие риски. Но глядя на информационное поле вокруг ЛЧИ и я понимаю, что сознание большинства полностью деформировано. Поэтому и выбрал цифру 15. Не много, не мало.
1 все в облиги а на купоны тарим колы
2 90% в облиги, остальное торгуем во фьючах — редкие сделки низкий риск и доходность в районе 1% в месяц
3 портфель по грэхему… 50%акции-50% облигации
1. Отложить немного своего генетического материала
2. Распродать все имущество, а также самого себя (на органы)
3. Положить все это бабло в банк
4. Оставить отложенный ордер на клонирование через 100 лет
5. Переписать завещание в пользу будущего клона
6. Терминироваться
По крайней мере у ДНК автора будет шанс )))
В следующий раз ждем очередной раздел Актуарные расчеты с использованием таблиц смертности и рекуррентных формул.
Во вторых им надо ухитриться протащить свои депозиты через великую депрессию и ряд последующих кризисов.
А закон такой — бедный человек так и останется бедным, даже если не будет ничего тратить, а только депозиты открывать. Вернее именно поэтому он и останется бедным.
Есть у Пушкина А.С.,-«Капитанская дочка», а там сказка(калмыцкая) про ворона и орла.
P.S. Аккурат подходит к нынешнему рынку.
чего то даже 10% не получается:)
Если обратить внимание на тэги, то можно заметить, что статья посвящена процессу познания. Следовательно, можно ожидать, что примеры слегка наивны, хотя ооочень близки к жизненной реальности.
Важно то, что многие просто не знают такие простые вещи, а посему не могут оценить их значимость.