Улыбка волатильности. Модель Бейтса
Продолжение. Начало в моем блоге и на сайте.
В прошлой статье про модель Хестона мы отметили, что она обладет недостатком, который проявляется в неточности определения цен опционов на малых сроках экспирации. Здесь мы рассмотрим модель Бейтса, в которой этот недостаток устранен, и она является одной из лучших аппроксимаций, описывающих поведение цен опционов для разных страйков и периодов до экспирации.
Модель Бейтса относится к моделям стохастической волатильности и определятся следующими уравнениями:
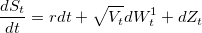
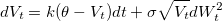
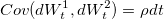
Как видите система уравнений почти идентична хестоновской, с теми же переменными: St, Vt- цена и волатильность базового актива, 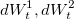 — случайные броуновские процессы с корелляцией, ρ,r,k,θ,σ- параметры модели (r=0 для маржируемых опционов). Разница в появлении слагаемого dZt, которое представляет собой Пуассоновский процесс с интенсивностью λ и лог-нормальным распределением скачков цены, независимым от
— случайные броуновские процессы с корелляцией, ρ,r,k,θ,σ- параметры модели (r=0 для маржируемых опционов). Разница в появлении слагаемого dZt, которое представляет собой Пуассоновский процесс с интенсивностью λ и лог-нормальным распределением скачков цены, независимым от 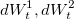 . Таким образом модель Бейтса является расширением модели Хестона с добавлением процесса скачков цены, что позволяет более точно воспроизвести реальный процесс приращения цены базового актива.
. Таким образом модель Бейтса является расширением модели Хестона с добавлением процесса скачков цены, что позволяет более точно воспроизвести реальный процесс приращения цены базового актива.
Если обозначить J размер скачка цены тогда:
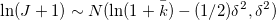 , для некоторого k¯, то есть процесс скачков имеет нормальное распределение со средним
, для некоторого k¯, то есть процесс скачков имеет нормальное распределение со средним 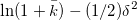 и дисперсией
и дисперсией 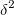 .
.
Тогда логарифимическое приращение цены базового актива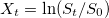 при условии риск-нейтрального подхода можно записать как:
при условии риск-нейтрального подхода можно записать как:
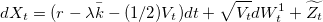
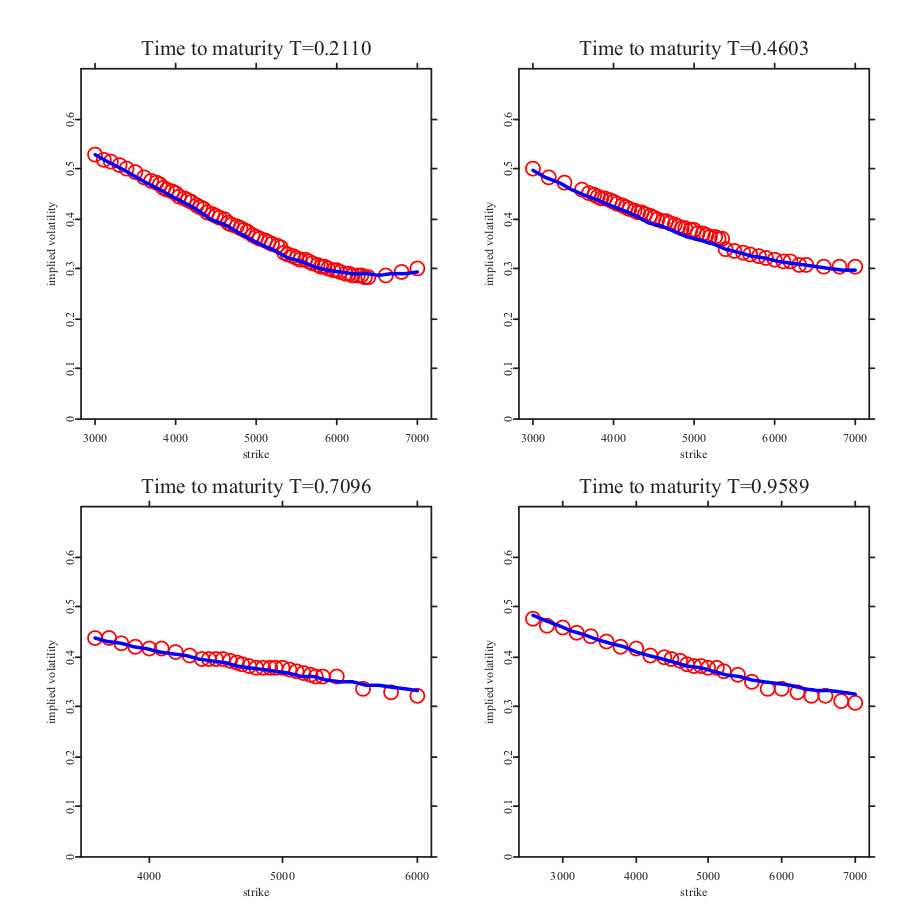
где Zt˜- Пуассоновский процесс с нормальным распределением величины скачков цены.
Для упрощения не буду приводить аналитическую формулу цены колл опциона для модели Бейтса, она схожа с хестоновской, желающие могут посмотреть, например, здесь. Сразу дам листинг вычисления этой цены на C#:
//a-нижний предел интеграла (равен 0)
//b - верхний предел интеграла. Выбирается значение от 100 до 200, в зависимости от нужной точности
//delta - вычисляется грек дельта, который равен значению Р1
double BatesCallGaussLegendre(double S, double K, double T, double r, double kappa, double theta,
double sigma, double lambda, double v0, double rho,
double a, double b, double muJ, double vJ, ref double delta)
{
// Числовое интегрирование
double[] int1 = new double[32];
double[] int2 = new double[32];
double y;
Complex om;
Complex i = new Complex(0.0, 1.0);
Complex Xk = new Complex(K, 0.0);
for (int k = 0; k <= 31; k++)
{
y = (a + b) / 2.0 + (b - a) / 2.0 * X[k];
om = new Complex(y, 0.0);
int1[k] = W[k] * (Complex.Exp(-i * Complex.Log(Xk) * om) * BatesCF(om - i, S, T, r, 0, v0, theta, rho, kappa, sigma, lambda, muJ, vJ) / (i * om * S)).Real;
int2[k] = W[k] * (Complex.Exp(-i * Complex.Log(Xk) * om) * BatesCF(om, S, T, r, 0, v0, theta, rho, kappa, sigma, lambda, muJ, vJ) / (i * om)).Real;
}
// Вектора интегральной суммы
double I1 = VectorSum(int1);
double I2 = VectorSum(int2);
// Определение P1 и P2
double P1 = 0.5 + 1.0 / Math.PI * I1 * (b - a) / 2;
double P2 = 0.5 + 1.0 / Math.PI * I2 * (b - a) / 2;
delta = P1;
// Цена колл опциона
return S * P1 - K * P2;
}
private Complex BatesCF (Complex phi ,double Spot, double T , double Rate, double Divd,double V ,double Theta , double Rho ,double Kappa, double Sigma ,
double Lambda , double MuJ , double VJ)
{
Complex S=new Complex(Spot , 0.0); // Цена базового актива
Complex r=new Complex(Rate , 0.0); // Безрисковая ставка (для маржируемых опционов =0)
Complex tau=new Complex(T , 0.0); // Период до экспирации в долях года
Complex i=new Complex(0.0 , 1.0); // мнимая часть комплексной переменной
Complex rho=new Complex(Rho , 0.0); // Параметр Бейтса: корелляция
Complex k=new Complex(Kappa , 0.0); // Параметр Бейтса: скорость возврата к средней
Complex vT=new Complex(Theta , 0.0); // Параметр Бейтса: уровень возврата
Complex lambda=new Complex(Lambda, 0.0); // Параметр Бейтса: интенсивность скачков
Complex sigma=new Complex(Sigma , 0.0); // Параметр Бейтса: среднеквадратичное отклонение волатильности
Complex v0=new Complex(V , 0.0); // Параметр Бейтса: текущая волатильность
Complex two=new Complex(2.0 , 0.0); // Число 2.0 в комплексной форме
Complex one = new Complex(1.0, 0.0); // Число 1.0 в комплексной форме
Complex muJ=new Complex(MuJ , 0.0); // Параметр Бейтса: средняя скачков ( в тексте k с верхним подчеркиванием)
Complex vJ=new Complex(VJ , 0.0); // Параметр Бейтса: дисперсия скачков
Complex q=new Complex(Divd , 0.0); // дивиденды (для опционов на фьючерсы =0)
Complex d = Complex.Sqrt (Complex.Pow(( rho * sigma * i*phi - k),2) + sigma*sigma * (i*phi + phi * phi));
Complex g2 = (k - rho* sigma *i*phi - d) / (k - rho* sigma *i*phi + d);
Complex cf1 = i*phi * (Complex.Log(S) + (r - q) * tau);
Complex cf2 = vT * k / ( sigma *sigma) * ((k - rho* sigma *i*phi - d) * tau - two * Complex.Log ((one - g2 * Complex.Exp(-d * tau)) / (one - g2)));
Complex cf3 = v0 / sigma *sigma * (k - rho* sigma *i*phi - d) * (one - Complex.Exp(-d * tau)) / (one - g2 * Complex.Exp(-d * tau));
// Составляющая для скачков цены:
Complex cf4 = -lambda*muJ *i*tau*phi + lambda*tau *( Complex.Pow((one+ muJ) ,(i*phi)) * Complex.Exp( vJ *(i*phi /two) * (i*phi -one) ) -one );
Complex cf = Complex.Exp(cf1 + cf2 + cf3 + cf4);
return cf;
}
//Функция суммирования элементов вектора
double VectorSum(double[] A)
{
double sum = 0;
double n = A.Length;
for (int i = 0; i <= n - 1; i++)
sum += A[i];
return sum;
}
Калибровка модели Бейтса аналогична калибровке Хестона, рассмотренной в прошлой статье. Однако в случае Бейтса нужно находить не 5 параметров модели а восемь: k,ρ,θ,σ,Vt,k¯,λ,δ2. Три последних параметра добавились от процесса скачков ( отмечу, что λ, упомянутая в статье о Хестоне имела другой смысл, чем параметр Бейтса — просто совпали обозначения). Это значительно усложняет нахождение глобального минимума и увеличивает время вычисления параметров модели. Здесь скорее всего уже не обойтись без применения алгоритмов поиска глобальных минимумов, типа Differential Evolution или ASA.
На графике в начале поста показана экстраполяция подразумеваемой волатильности опционов на индекс DAX, вычисленной по модели Бейтса для разных сроков до экспирации. Как вы можете заметить, даже на периодах, близких к экспирации, модель хорошо воспроизводит рыночные цены опционов ( выраженных через волатильность из формулы Блэка-Шоулза).
Это последняя модель, рассмотренная в цикле статей про улыбку волатильности. На моей практике она оказалось лучшей из множества применяемых мной моделей на российском рынке, поэтому рассмотрение остальных существующих аппроксимаций цен опционов не имеет особого смысла.










W = new double[32];
X = new double[32];
int info = 0;
alglib.gqgenerategausslegendre(32,out info, out X, out W);
32 — это количество узлов вычисления ( этой цифры достаточно для точности)
W — веса, X — узлы
Вот прямо только что хотел спросить! :)
надо что нибудь попроще… тут пересекается — покупаем, тут зашло за уровень 100 — продаем… а так думаю 99.9% на смартабе вас не поймут ))
и вообще не понимаю, почему с такими познаниями вы еще не в списке форбс ну или как минимум в какомнибудь крутом американском хедж фонде…?
а на что тогда надеятся нам смертным
Какое отношение теория эффективного рынка имеет к созданию сабпраймов? Истинные причины кризиса 2007-2008 отлично изложены в книге Майкла Льюиса «Большая игра на понижение. Тайные пружины финансовой катастрофы», а «притягивание за уши» к тем событиями опционных квантов не более PR автора. Вот кванты, сидевшие на обосновании CDO, да, приложили руку. Но эти кванты и теория эффективного рынка — это «разные планеты».
Нормальность никак не связана с эффективностью рынка. Рынок может быть нормальным и неэффективным, а может быть ненормальным и эффективным. Предложенная модель как раз для второго случая. Она объясняет «тяжелые хвосты» одномерного распределения (причем любой экспоненциальной «тяжести»), любую «улыбку волатильности», но при этом остается в рамках гипотезы эффективности.
А LTCM рухнул из-за огромного плеча, которое к теории эффективности-неэффективности не имеет никакого отношения.
Проверка на знание темы: в позициях на каких инструментах «погорел» LTCM?
Вы явно не в теме: LTCM — торговал спредами доходностей облигаций и «погорел» на расхождении спреда между доходностями развитых и развивающихся стран. А теперь подумайте, если позиция без плеча, то можно ли обанкоротиться на спредовой торговле?
Это все хорошо описано вкниге Скотта Паттерсона.
PS. США Японию и страны Европы можно отнести к развитым странам.
Из Вашего же текста следует, что причина коллапса — левердж, а их модель статистического арбитража ставок (!) — лишь причина убытков, размер которых и зависит от левереджа. Без леверджа позиции LTCM и 10% убытков не давали. Разве 10% убытков могут вызвать коллапс?
Большой убыток фонд получил от арбитражной позиции по DLC ( dual listing company) между Royal dutch shell И Shell. Премия Royal dutch к Shell'у выросла с 8 до 22%. Из-за увеличивающихся убытков фонд ликвидировал эту позицию с гигантским убытком, хотя вполне возможно на долгосроке, стратегия фонда принесла бы плюс. И понеслась.
«When Genius Failed: The Rise and Fall of Long-Term Capital Management» книга Роджера Ловенстайна. Почитайте.
Во-первых, они торговали спредами доходностей облигаций развитых и развивающихся стран, но там позиции были некритические ко всему объему капитала (только позиция в ГКО-ОФЗ России оценивалась в 250 млн. долларов). Но я утверждал другое: расширение этого спреда привело к убыткам по всем их спредовым позициям на облигациях, составлявших все вложения фонда.
Во-вторых, именно из теории эффективного рынка следует, что левередж выше некоторой границы рано или поздно «убьет» любой счет. Например, именно плечо 1:100 и дает статистику 95% сливов депозитов на forexe в строгом соответствии с теорией эффективного рынка. Если б на паре доллар-евро плечо на этом рынке было бы не больше 1:20, то теория эффективного рынка говорит о том, что сливших депозит было бы меньше 50% и именно такой процент мы видим у брокеров на срочных рынках.
В-третьих, именно нобелевские лауреаты настаивали на фиксации убытков в 40%, когда стало понятно, что уровень левереджа перешел эту границу, и после отказа Меривезера сделать это, вышли из состава партнеров фонда. Все дальнейшие усреднения и увеличение левереджа — это личные решения Меривезера.
И наконец, в-четвертых, после дофинансирования фонда консорциумом, созданным под эгидой ФРС, и закрытия позиций в 1999-2000-м все участники консорциума получили прибыль.
По поводу кредитного плеча и сливов. Откуда у вас уверенность и такие цифры по этому поводу? никаких официальных исследований не проводилось по этому поводу. Это мы понимаем эмпирически. Вы как то плаваете в теории статистике, чтобы так оголтело обосновывать такие глобальные проблемы. Я вам могу объяснить позицию фонда их позиции левериджа нормальным языком, а не теми наборами терминов что бросаетесь вы. ОНи считали риск левериджа, который они используют в торговле, существенно ниже риска обвала спредов, в миллиарды раз. Их теория это утверждала исходя из допущений нормального распределения скачков цен. Вот и все.
А вот это «именно из теории эффективного рынка следует, что левередж выше некоторой границы рано или поздно «убьет» любой счет» это вообще нереальная бредятина. Где это написано? Гипотезу Эффективного Рынка сформулировал Юджин Фома. Где он что то подобное писал? Главная аксиома Эффективного Рынка это что в цене актива уже учитываются все события прошлые и настоящие. У меня складывается ощущение что увас в голове нереальная каша из левериджа, спредов, вероятности слива, нормального распределения, Эффективного Рынка, и прочих мало понятных вам слов.
По поводу цифр. 95% сливов депозитов на forexe — это по утверждениям «знающих» людей. Я действительно не знаю этой цифры, но именно исходя из теории эффективного (математически правильнее сказать мартингального) рынка для пары евро-доллар при плече 1:100 так и получается. Если там реально гораздо меньше сливших хотя бы один раз депозит при таком плече, то я рад за участников — рынок неэффективен. Только исходя из «кухонности» форекс-бизнеса, мне кажется, что начинать его без прогноза слива у 90% как то бессмысленно.
А теория разорения на случайном блуждании изложена в самых простейших учебниках по финансовой математике. На ней основана страховая индустрия. И если б Вы хоть чуть-чуть были знакомы с математической статистикой, то знали бы, что достижение критического уровня означает, что модель не верна и дальнейшие действия в ее рамках проводиться не должны. Потому то и партнеры Меривезера, знакомые с этим настаивали на фиксации 40% убытка. А дальнейшая история LTCM — это уже история из области психологии, а не финансовой математики.
И еще раз подчеркну: нормальность и эффективность — вещи несвязанные.
Я не говорю, что теория эффективного рынка верна, так как знаю кучу статистических доказательств обратного, но именно в расчете критического уровня левержджа она «рабочая», в том смысле, что его нельзя преодолевать. Вся проблема в психологии: этот критический уровень достигается тогда, когда на счете убытки, которые не хочется фиксировать и начинается усреднение с увеличением левереджа. В России, кстати, был аналогичный пример — фонды Юниаструма, погоревшие на плече в РЕПО с облигациями.