Скрытые возможности
Рассмотрим интересный пример, на первый взгляд имеющий мало общего с финансовыми рынками.
Игроку предложено бросить игральную кость 5 раз подряд, при этом он может остановиться в любой момент и получить столько долларов сколько выпало очков в последнем броске. Сколько заплатит нейтральный к риску игрок за возможность участвовать в такой игре?
Такие задачи из теории игр следует решать с конца, по алгоритму Цермело.
Допустим, у нас осталась всего одна попытка. Тогда, как легко подсчитать, в среднем можно получить 3.5 доллара. т.е., если такой эксперимент повторять много раз, средний выигрыш игрока будет стремиться к 3.5 – математическому ожиданию игры.
Это и есть риск-нейтральная цена игры, состоящей только из одной попытки.
Что, если осталось две попытки? Игрок уже знает, что для последней попытки цена игры равна 3.5, поэтому он должен сравнивать число, выпавшее в предпоследней попытке, с этой цифрой и выбирать большее значение. Т. е., если, например, выпадет «2», он должен попытаться еще раз. Если «4» — не станет и выйдет из игры. Какова тогда цена игры, состоящей из 2-х попыток? Нужно опять провести усреднение по равновероятным исходам, только теперь уже для ряда 3.5, 3.5, 3.5, 4, 5, 6. (Мы выяснили, что при выпадении 1, 2 или 3 игрок продолжит игру, и заменяем эти значения на 3.5 – ценой последующей игры) Получится 4.25.
Продолжая эти рассуждения далее от конца к началу, легко установить, что игрок всегда должен сравнивать результат выпавшей кости с ценой игры на последующем ходе.
В итоге мы получим такой ряд справедливых цен: 3.5, 4.25, 4.67, 4.94, 5.13. Последнее число и есть искомое решение задачи.
Как посчитать справедливую цену игры методом обратной индукции стало понятно, но как в нее играть, какова оптимальная стратегия? Ведь люди играют не от конца к началу, а наоборот.
Игрок при каждом броске должен сравнивать выпавшее число со справедливой ценой для данного шага (в обратном порядке) Допустим, игрок делает 1-й бросок в игре из 5 возможных ходов. Если выпало 6 – останавливается (6 > 5.13), нет – продолжает. При втором броске останавливается, только если выпадет 5 или 6. И так далее.
Интуитивно понятно, что если игроку предоставляется огромное количество попыток, то вероятность выпадения «6» очень велика. И он должен заплатить сумму, практически равную 6. Если ему сказать — бросай сколько хочешь, он и будет бросать пока не выпадет 6. Распределение исходов игры биномиальное и легко подсчитать, что вероятность выпадения хотя бы одной «6» в n попытках равна 1- (5/6)^n Если попыток 1000, то и вероятность почти не отличается от 1.
Алгоритм расчета легко реализовать в R:
a<-c(1,2,3,4,5,6)
fair_price<-function(n) {
for (i in 1:n) {
a<-pmax(a,mean(a))
}
print(a[1])
}
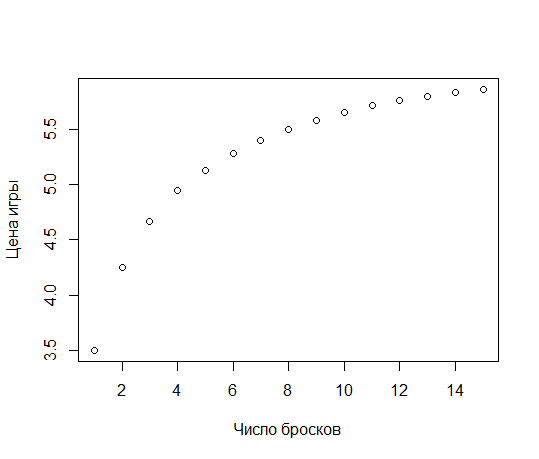
Можно построить график справедливой цены игры в зависимости от предоставленного количества бросков, из него видно, что с ростом числа предоставленных попыток цена плавно стремится к 6.
Стоит отметить и предельные случаи – игрок с абсолютным отвращением к риску заплатит 1 доллар, чтобы быть как минимум в безубытке при любом исходе серии испытаний. Рискофил заплатит все 6, так как будет уверен, что ему обязательно повезет.
Данная задача интересна не только как забавный пример из теории вероятности и теории игр, но и как ключ к пониманию расчета стоимости опциона американского типа, т.е. когда его исполнение – в данном случае выход из игры – возможно в любой момент. Если бы игроку поставили условие, что выходить нельзя, и деньги можно получить только за последний бросок, то в силу независимости испытаний цена игры очевидна – это 3.5. Вероятность получить «6» (так же как и «1», «2», «3»..) одинакова в любом из бросков и не зависит от предыдущих исходов.
Но если у игрока есть опция выхода, мы получаем добавочную стоимость [5.13-3.5] = 1.63. Это и будет внутренней стоимостью «опциона на выход» из игры в 5 возможных ходов.
Теперь можно перенести это понимание на торговлю на фондовом рынке. В любом инструменте или стратегии могут быть вшиты скрытые реальные опционы, которые нужно обнаружить и использовать (купить недооцененное, продать переоцененное) Самый простой модельный пример – покупка акции, если безрисковая ставка, как и вероятность банкротства компании, равна нулю (понятно, что так не бывает) Какова оптимальная стратегия торговли? Если продолжать аналогию с игральной костью, то ежедневные рыночные цены – это сыплющиеся на трейдера реализации исходов в игре с очень большим количество ходов. И вывод очевиден – в таких условиях (когда деньги дают нулевую доходность) ничто не переиграет стратегию «купил и держи», т.е. купленную акцию вообще нельзя никогда продавать, так как всегда остается возможность еще более высокой цены, когда-нибудь, в светлом будущем. Правда, сразу становится видна некоторая абсурдность ситуации, ведь если никто не будет продавать, то не будет и рынка. В реальной жизни безрисковые ставки ненулевые и держать акцию, застрявшую в рендже, становится слишком накладно.