05 февраля 2022, 14:27
НЛМК, Решение задачи прогнозирования изменения запасов через системы линейных уравнений. (Часть 1)
Всем привет,
Недавно я опубликовал пост-анализ расчетов дивидендов за 4-й квартал от 30 ноября 2021, где основное упущение было непонимание до конца — что влияет на изменение инвентаризационных запасов и в какой степени?
Нас интерисут строка Increase in inventories/(Увеличение запасов)

При существенный волатильности цен ± 15% на сырьевую корзину или готовую продукцию, можно получить уменьшение свободного денежного потока (СДП/FCF) до 40% от EBITDA.

Об этом ярко говорит график Increase in inventories of EBITDA percent/Увеличение запасов от EBITDA в процентах, где изменение запасов может как увеличить EBITDA на 40% так и уменьшить на 30%
В случае НЛМК из сырья можно выделить Уголь, ЖРС материалы и лом, как наиболее затратные и волатильные.

Так же в состав запасов войдет вся стальная продукция предназначенная для продажи.
И итого, что бы подсчитать стоимость запасов нам необходимо по каждому из пунктов количество умножить на соответствующую стоимость, где каждый квартал — это отдельное линейное уравнение. А как мы знаем из школы, для решения системы линейных уравнений число уравнений должно превышать число неизвестных.
Выпишем неизвестные переменные:
1. Xп - количество запасов готовой(непроданной) продукции в тоннах
2. Xу - количество запасов угля в тоннах
3. Xж - количество запасов ЖРС в тоннах
4. Xл - количество запасов лома в тоннах
5. Xс - постоянные запаса на другие материалы и строящиеся объекты
Далее предположим, что запасы количественно квартал к кварталу существенно не изменяются в своих пропорциях. (Например угля всегда 30% от всего сырья)
Тогда затраты на материалы на тонну продукции станут коэффициентами a, а суммарная инвентаризационная стоимость запасов — b мы получим следующую систему линейных уравнений(СЛУ)

Так же для удобство преобразуем нашу СЛУ в матричный вид и подставим значения коэффициентов за Q3 2020(a1), Q4 2020(a2), Q1 2021(a3), Q2 2021(a4), Q3 2021(a5), а Q4 2021 используем для проверки полученного решения.

Запишем
М — матрицу коэффициентов, где затраты поделим на продажи
B — вектор свободных решений (Balance Sheet/Current assets/Inventories)
A - матрицу коэффициентов за Q4 2021 для проверки решения

Далее с помощью функции lsolve получим первое грубое решение и выполним проверку:
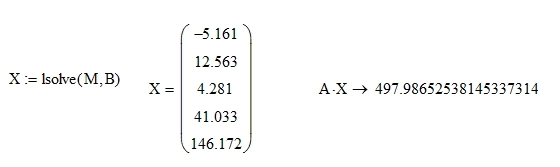
Так как при записи СЛУ мы сделали ряд давольно грубых допущений, то получили уменьшение запасов на $498 млн., против фактического увеличения на $513 млн.
Далее попробуем добавить компенсаторов, как минимум для непроданной продукции и умножим на себестоимость

Q3 2020 -0,620 млн.
Q4 2020 -0,357 млн. т,
Q1 2021 +0,399 млн. т
Q2 2021 +0,193 млн. т
Q3 2021 -0,280 млн. т
Q4 2021 +0,032 млн. т

Получили довольно большой разбег от $2649 млн. запасов в оборотном капитале и ошибка составила более 15%, но уже дает понятие об направлении изменений.
Далее заглянем в примечание отчета по МСФО за дополнительной информацией в запасах и попробуем декомпозировать задачу

И отдельно посчитаем сырье, незавершенное производство, готовую продукцию и добавим напрашивающийся компенсатор для производства стали, но уже во второй части.

P.S. Присоединяйтесь к моему Telegram-канале https://t.me/self_investing. Графики доступны на моем сайте, где принимаются донаты yoomoney.ru/to/41001568160963 на развитие канала и сайта.
Недавно я опубликовал пост-анализ расчетов дивидендов за 4-й квартал от 30 ноября 2021, где основное упущение было непонимание до конца — что влияет на изменение инвентаризационных запасов и в какой степени?
Нас интерисут строка Increase in inventories/(Увеличение запасов)

Почему это важно ?
При существенный волатильности цен ± 15% на сырьевую корзину или готовую продукцию, можно получить уменьшение свободного денежного потока (СДП/FCF) до 40% от EBITDA.
Об этом ярко говорит график Increase in inventories of EBITDA percent/Увеличение запасов от EBITDA в процентах, где изменение запасов может как увеличить EBITDA на 40% так и уменьшить на 30%
Постановка задачи
И так обратимся для начала к теории учета по МСФО:
В состав запасов входят активы:
- предназначенные для продажи в ходе обычной хозяйственной деятельности;
- незавершенное производство;
- сырье и расходные материалы;
- объекты нематериальных активов, которые создаются для целей продажи;
- объекты имущества, приобретенные или строящиеся для целей продажи или перепродажи в ходе обычной хозяйственной деятельности предприят
В случае НЛМК из сырья можно выделить Уголь, ЖРС материалы и лом, как наиболее затратные и волатильные.

Так же в состав запасов войдет вся стальная продукция предназначенная для продажи.
И итого, что бы подсчитать стоимость запасов нам необходимо по каждому из пунктов количество умножить на соответствующую стоимость, где каждый квартал — это отдельное линейное уравнение. А как мы знаем из школы, для решения системы линейных уравнений число уравнений должно превышать число неизвестных.
Выпишем неизвестные переменные:
1. Xп - количество запасов готовой(непроданной) продукции в тоннах
2. Xу - количество запасов угля в тоннах
3. Xж - количество запасов ЖРС в тоннах
4. Xл - количество запасов лома в тоннах
5. Xс - постоянные запаса на другие материалы и строящиеся объекты
Далее предположим, что запасы количественно квартал к кварталу существенно не изменяются в своих пропорциях. (Например угля всегда 30% от всего сырья)
Тогда затраты на материалы на тонну продукции станут коэффициентами a, а суммарная инвентаризационная стоимость запасов — b мы получим следующую систему линейных уравнений(СЛУ)

Решение системы уравнений
Так как я уже не молод и ленив, то решать будем с помощью известного инструмента MatchCad в узких кругах(скачаем и установим).Так же для удобство преобразуем нашу СЛУ в матричный вид и подставим значения коэффициентов за Q3 2020(a1), Q4 2020(a2), Q1 2021(a3), Q2 2021(a4), Q3 2021(a5), а Q4 2021 используем для проверки полученного решения.

Запишем
М — матрицу коэффициентов, где затраты поделим на продажи
B — вектор свободных решений (Balance Sheet/Current assets/Inventories)
A - матрицу коэффициентов за Q4 2021 для проверки решения

Далее с помощью функции lsolve получим первое грубое решение и выполним проверку:
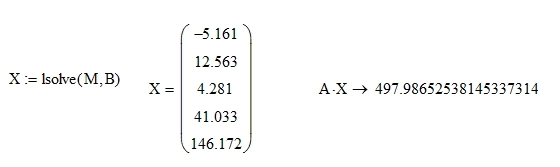
Так как при записи СЛУ мы сделали ряд давольно грубых допущений, то получили уменьшение запасов на $498 млн., против фактического увеличения на $513 млн.
Далее попробуем добавить компенсаторов, как минимум для непроданной продукции и умножим на себестоимость

Q3 2020 -0,620 млн.
Q4 2020 -0,357 млн. т,
Q1 2021 +0,399 млн. т
Q2 2021 +0,193 млн. т
Q3 2021 -0,280 млн. т
Q4 2021 +0,032 млн. т

Получили довольно большой разбег от $2649 млн. запасов в оборотном капитале и ошибка составила более 15%, но уже дает понятие об направлении изменений.
Далее заглянем в примечание отчета по МСФО за дополнительной информацией в запасах и попробуем декомпозировать задачу

И отдельно посчитаем сырье, незавершенное производство, готовую продукцию и добавим напрашивающийся компенсатор для производства стали, но уже во второй части.

P.S. Присоединяйтесь к моему Telegram-канале https://t.me/self_investing. Графики доступны на моем сайте, где принимаются донаты yoomoney.ru/to/41001568160963 на развитие канала и сайта.










Ввели кэфы вместо ежеквартального прогнозирования на долгосрочной основе. Опасно.