Биржа  -  это не волшебная палочка, не тайная комната, не платяной шкаф и совершенно не ошибка в «матрице», невиданным образом превращающая бедных в богатых, а богатых, соответственно, в бедных. Нет, от функционирования биржи выигрывает только  сама биржа. Для игрока же биржа — это всего лишь игра с нулевой (отрицательной) суммой и можно ловить на ней удачу, в расчёте вытащить выигрышный «лотерейный билет», после чего навсегда покончить с этим, а можно попытаться построить на бирже «свой бизнес» — о чём и повествует книга. 

Книга написана профессиональным языком, содержит большое количество отсылок к статистическим данным и опыту профессиональных финансовых управляющих, заслуживает наивысшей оценки и рекомендуется самому широкому кругу читателей.

По мотивам последних обсуждений.






Куда унесёт нас ураган? Выдержат ли паруса? Оставит ли в живых злая буря свою новую игрушку? Так спрашивает себя каждый капитан перед дальним плаванием, расслабившись за игрой в орлянку.




( Читать дальше )

Сегодня мы будем выступать в качестве поставщика бесконечной ликвидности по опционам. То есть мы будем безотказно играть в игру с нулевой суммой так, чтобы, как минимум, не проиграть, а это возможно только в том случае, если мы будем продавать и покупать волатильность по цене, соответствующей седловой точке в игре покупателя и продавца, то есть по цене GTO (game theory optimal). Иными словами, мы будем заниматься непосредственно pricing'ом опционов, назначая цены put'ам и call'ам, таким образом, чтобы ни одна стратегия и ни один набор случайных, стохастических стратегий не мог получить положительное преимущество при игре с нами.

Чтобы назначать цену волатильности, для начала, не плохо было бы принять какую-либо модель волатильности. Например, это может быть модель случайного процесса, подчинённого логистическому распределению:


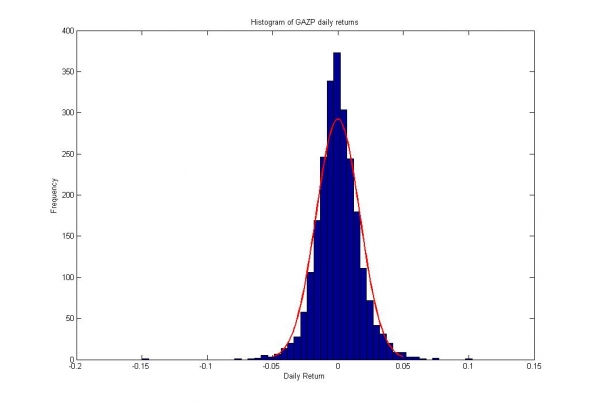
Рис.1. Распределение логарифмических приращений цен акций ПАО Газпром и их аппроксимация логистическим распределением.


или распределению Лапласа:

( Читать дальше )

Вопрос:

Проведена симуляция покупки опционов Call за день до экспирации по страйкам +0%, +2%, +5%, +8% от центрального  — по прогнозным ценам и в целях проверки модели справедливого ценообразования.





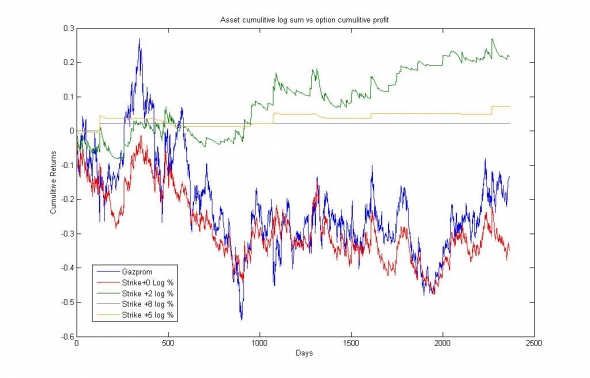
Ev[ +0%] и Ev[ +2%] располагаются на границе доверительного интервала, но по разные стороны.
Требуется ответить на вопрос IV=RV?  Уместен ли t-test?

Занимаясь первоначально исключительно портфельным инвестированием мы всё чаще сталкиваемся с задачей моделирования волатильности фондового рынка и его будущих ковариаций. Соответственно,  так или иначе, мы сталкиваемся с проблемой выбора модели, которая позволяла бы нам на самом широком диапазоне данных получать сколько-нибудь значимые оценки. 


В качестве показателя качества моделей нами была выбрана доля объяснённой дисперсии:





и промоделирована ошибка измерения волатильности заданного стационарного процесса на интересующем нас интервале: 




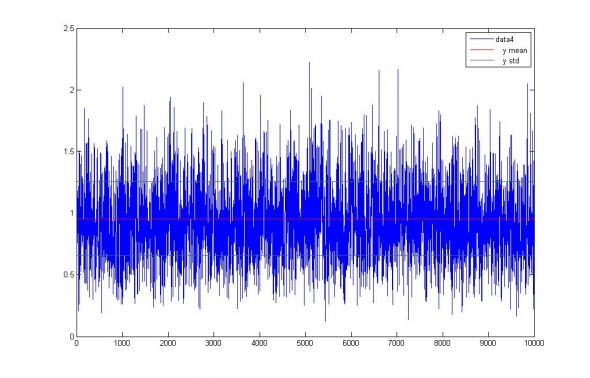
( Читать дальше )

Дополнение к серии «Портфельная оптимизация как бустинг на слабых моделях»

• Обобщённая проблема

Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.

Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:


 

где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.

( Читать дальше )

Устойчивые долгосрочные модели


В предыдущих частях (часть 1, часть 2) мы рассмотрели построение композитных систем оценок ценных бумаг, построенных при помощи распространённых средств машинного обучения (Bag/Boost методы). Однако, такой подход, несмотря на все свои преимущества (скорость, точность) имеет ряд больших недостатков – отсутствие универсальности моделей в результате проблем «переобучения»  (точной настройки на определённые типы рынков и временные интервалы) и сложность интерпретации полученных композиций.

В результате решения этих проблем мы разработали базовую модель на основе наших представлений о стохастических дифференциальных уравнениях с квантовыми скачками, образующих улыбку волатильности. Эта макромодель получила в наших исследованиях наиболее полную микроскопическую интерпретацию.

( Читать дальше )

Краткое описание эффекта тут.

Постулат:

Худшее, что может сделать инвестор — купить облигации казначейского займа. Потому что в дополнение к отрицательной реальной, а часто и номинальной, доходности, он получает ещё бесконечный «не-рыночный» риск.

И если бы капиталистическая «рыночная» экономика изначально (со времён А.Смита) не была построена на добровольно-принудительном исполнении чужой воли, то долговой рынок государственного казначейского займа был хоть сколько-нибудь конкурентоспособным, то есть, непосредственно, рыночным.


Условия задачи:

В 2018 году вы должны держать UST на 2 трлн. долларов.
В 2019 году вы должны будете  держать UST на неопределённую сумму от 1 до 3 трлн. долларов.

Модель:

В случае, если вы обладаете уверенностью относительно требований к вам по удержанию в своём «портфеле» UST в размере 2 трлн. долл. в будущем, то все облигации различных дюраций будут для вас индифферентны (задержками выплат, комиссиями и пр. мы пренебрегаем). В этом случае кривая доходностей имела бы свою безарбитражную форму, выраженную константой (т.н. «плоская кривая»):

( Читать дальше )

• SP500 против денежной массы безналичных, ликвидных коммерческих денег.

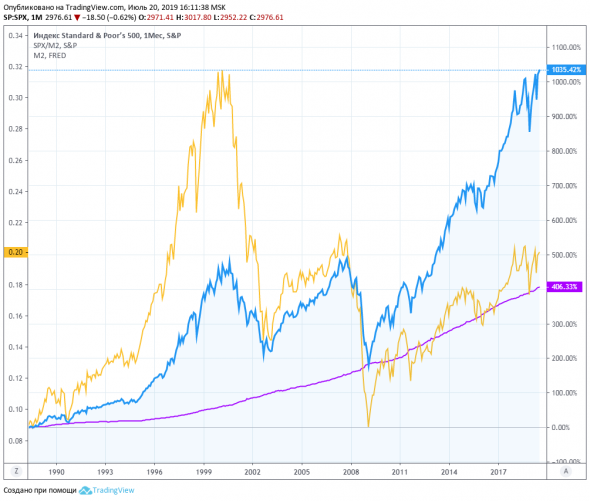
SPX — синяя кривая, M2 — фиолетовая, SPX/M2 — желтая.

• Nasdaq 100 против всё той же массы коммерческих денег :

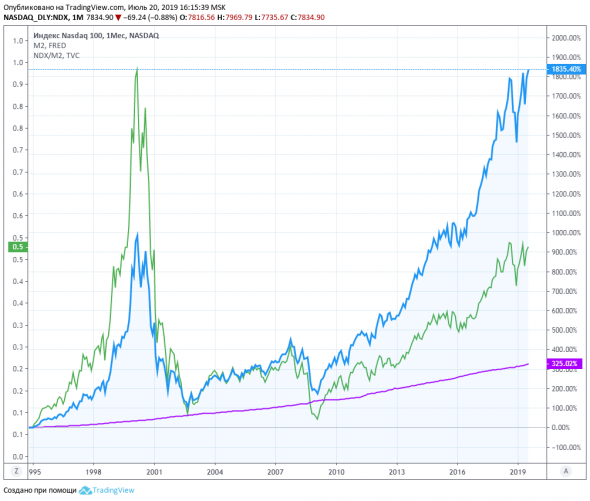
( Читать дальше )

      В свете интереса к моим работам в области оценки рисков нестационарных объектов со стороны опционов и возникшего вопроса о применимости к анализу финансовых временных рядов методов классического статистического анализа проведём маленький численный эксперимент:

• Оценим АКФ акций ПАО Сбербанк за последние 8 лет :

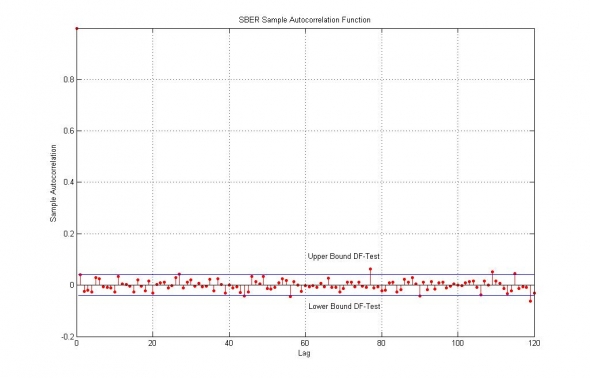
Рис. 1. Тест Дики-Фуллера и автокорреляционная функция логарифмических приращений цен акций ПАО Сбербанк.


Как видно из теста, никаких трендов (англ. тенденций, закономерностей) на акциях Сбербанка классической математической статистикой не обнаружено и все АК коэффициенты лежат в пределе статистической погрешности при измерении нуля.


Однако, тест Дики-Фуллера, с одной стороны, разработан для стационарных, не-локализованных процессов и отражает только отсутствие трендов в среднем по времени, а с другой — проводится совершенно с другими целями выявления детерминированных сезонных и/или растущих тенденций, а не стохастических оценок рисков. В этом смысле мы будем интерпретировать АКФ не по-классически, детерминированно, а как функцию искажения случайности.

( Читать дальше )