Дмитрий Шихалев
Сегодня в доллар/рубль
- 15 февраля 2017, 20:58
- |
Дополнительно: Вчера в последние два часа сессии были агрессивные покупки 57000 страйка путов. Это было видно из таблицы обезличенных сделок, где инициатором был покупатель. Была набрана поза около 20000 штук по цене 50-70 рублей.
А сегодня были следующие события.
На вечерке цена максимально приблизилась к 57500 страйку, вызывая у продавцов путов сильное волнение. И начало сессии показало, что не зря.
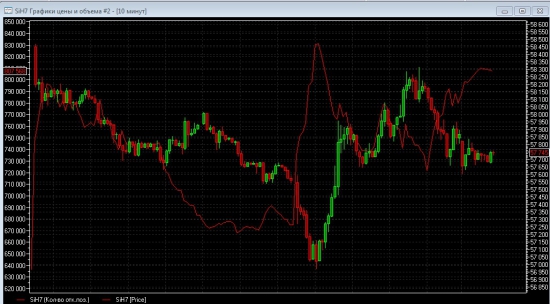
Сессия началась точно также как и вчера с роста ОИ на 130 000 контрактов в течении часа.
После первой красной свечи до 57360 в продажу фьючей подключились продавцы путов 57500 страйка для страховки своей позы, влив в рынок около 20000 контрактов.
Когда цена дошла до 57000 в игру вступил продавец 57000 путов.
Причем он начал действовать очень грамотно(видимо поставка фьючей не входит в его планы). Он «выдавил» продавцов фьючей не просто от 57000 страйка, а пошел выше — к 57500 и закрепил цену выше 57500. Тем самым заставил продавцов 57500 путов развернуть свою позу в сторону выкупа всех проданных фьючей.
( Читать дальше )
- комментировать
- ★11
- Комментарии ( 36 )
Что сегодня происходило в Доллар/рубль?
- 14 февраля 2017, 22:32
- |
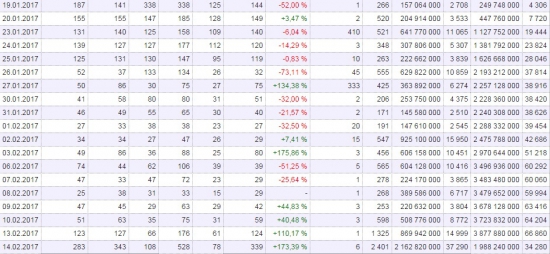
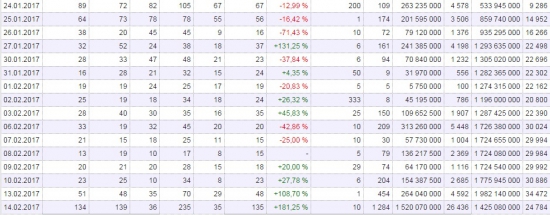
Если бы мы вчера вечером или с утра посмотрели на опционную доску февраль SIH7, то увидели бы, что:
в страйке 58000 открытых позиций было 66860 контрактов,
в страйке 57500 открытых позиций было 34472 контракта,
в страйке 57000 открытых позиций было 59066 контракта.
Если рассмотреть структуру набора позиций в этих страйках, то можно сделать вывод, что:
— в 58000 и в 57500 страйке набор позиций был равномерен начиная с конца января. Это говорит о том, что и продавцы и покупатели опционов было много независимых друг от друга участников,
( Читать дальше )
Технический индикатор РТС на основе данных MOEX и USD/RUB
- 29 января 2017, 18:59
- |
Недавно, были дебаты Опционного математика и Опционного не математика по поводу:
«Нужна ли математика в опционной торговле» каждый наверное сделал свой вывод.
Я приведу пример, как использовать элементарную математику в прогнозировании стоимости РТС, не глядя даже на его график.
Нам нужен график доллар/рубль и график ММВБ
Давайте назовем функцией Y(t) — график USD/RUB, а график ММВБ — X(t)
Таким образом, всегда будет выполнятся равенство Y(t) = A*X(t) + B
Наша задача найти B — это и есть ошибка(отклонение) двух функций.
Для начала находим А:
Возьмем ограниченный период 5-ти ближайших торговых дней.
Имеем y(t)1 и y(t)5, x(t)1 и x(t)5
Используя знания о геометрическом свойстве Интеграла:
Проинтегрируем функцию Y(t) от y(t)1 до y(t)5
Проинтегрируем функцию X(t) от x(t)1 до x(t)5
A = Интеграл Y(t) от y(t)1 до y(t)5 / Интеграл X(t) от
( Читать дальше )
Можно ли спрогнозировать даты "шторма" на рынке? Да, через ОФЗ-ПК!
- 24 ноября 2016, 19:47
- |
Это - Облигации федерального займа с переменным купоном
Облигации федерального займа с переменным купоном (ОФЗ-ПК) – среднесрочная ценная бумага. Выпуск ОФЗ-ПК регламентируется постановлением Правительства РФ от 15 мая 1995 г. № 458 «О Генеральных условиях выпуска и обращения облигаций федеральных займов». Банк России является генеральным агентом эмитента. Через его учреждения или уполномоченные им организации осуществляются все операции по размещению и обращению облигаций на рынке ценных бумаг, включая выплату купонного дохода, погашение за счет средств эмитента и учет прав на облигации. Выпуск, обращение и погашение ОФЗ-ПК осуществляется на ММВБ и подключенных к ней региональных площадках по схеме, аналогичной схеме ГКО.(Справка)
Самое важное в ОФЗ-ПК — это переменный купон. Именно это и определяет наиболее существенные особенности в обращении и обслуживании ОФЗ-ПК.
( Читать дальше )
Кто то, все таки решил манипулировать рынком RVI!
- 02 ноября 2016, 20:10
- |
Он начал продавать фьючерс RVI_11.12 по 28.5п. При RVIindex = 23п.
Его прибыль бы соответствовала 28.5-23=5.5п. что соответствовало бы = 11 долларов на 1 контракт.
На продавал он там до… на.
Тут откуда не возьмись появилась вола. RVI взлетел до 25п. а RTSVIX в какой то момент был больше RVI, что в последнее время редкость.
Что делает наш игрок? Он просто выставляет айсберги на 28п. по 100 и 200шт. заявок. Цель, чтобы никто не смог пробить его позу.
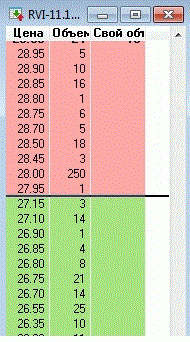
Ликвидность низкая и все, кто думает, что он купил волатильность и с ростом волатильности RVI пойдет вверх — нет. Наш игрок все выкупит, и дождется когда Фьючерс на RVI и индекс на RVI сравняются и получит прибыль или минимальный убыток.
Справка: Фьючерс на RVI — это копия VIX он рассчитывается как variens svop, то есть он по определению в контанго от индекса RVI, и чем дальше тем сильнее.
( Читать дальше )
Вопрос который поднимает ЦБ уже давно решен биржей.
- 24 сентября 2016, 22:33
- |
Когда возникает неопределенная ситуация — биржа на срочке поднимает ГО и участники не могут переборщить с позициями. Несогласных режут.
Трейдер сокращает позу или входит так чтобы ГО уменьшилась.
По сути, людям неопытным брокер может поставить ГО по инструментам какое угодно. Тем самым ограничивая риски потери капитала новичкам.
Новичок, через предоставление квалификационного аттестата и пр. может доказать брокеру, что он не новичок! Биржа вообще о «новичке» знает все! Сколько он внес, сколько потерял, сколько заработал, и т.д., про аттестат только не знает!
Наличие квалификационного аттестата не значит наличие опыта торговли на рынке. Это факт! Аттестаты получают для принятия на работу и пр. Человек может и не быть принят на работу трейдером, но у него есть аттестат. Через год он вообще не помнит что сдавал. Его целью было сдать и закрепить на практике, а практика не пришла...
Сумма капитала никогда не равнялась опыту его эффективного управления.
( Читать дальше )
Открытый интерес по нефти. Спекулянты ждут прорыва 28-38
- 08 февраля 2016, 20:52
- |
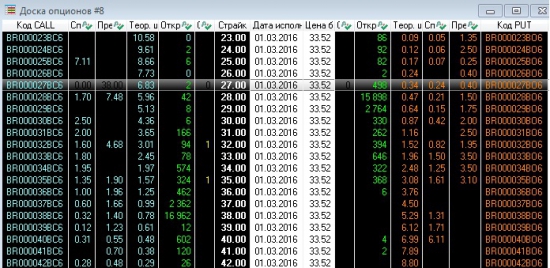
Судя по сильным движениям нефти спекулянты купили опцики по 38 — 16962 и по 28 — 15989 на 1 марта 2016г… Те кто им продал тоже понятны, Коллы продали те кто покупал по 30 и ниже(фиксят прибыль), Путы продали те кто хочет купить по 28, для них это приемлемая цена. То есть спекули планируют, что к 1 марту сего года нефть будет стоить или выше 38 или ниже 28 долларов за барелль))
Зависимость динамики изменения доходности Трежерис и кризисов. (Не волновая теория)
- 14 сентября 2015, 09:16
- |
Вот здесь:stockcharts.com/freecharts/yieldcurve.php
Если включить анимацию видно, что кризисы начинались тогда когда ставка по коротким трежерям превышала ставку по длинным.
Начало кризиса:
( Читать дальше )
теги блога Дмитрий Шихалев
- cboe skew
- EU
- MOEX
- ODVA
- Ri
- RTS
- RVI
- S&P500
- Si
- Акрон
- Акции
- Апатит
- АФК Система
- Аэрофлот
- Башкирэнерго
- Башнефть
- Белон
- Биннофарм
- биткоин
- Великая Отечественная война
- волатильность
- второй эшелон
- газпром
- гуру
- Детский мир
- дивергенция
- Доллар
- Дорогобуж
- женщины
- Иванов
- индекс ММВБ
- индекс оптимизма
- индикаторы
- интервью
- история
- ключевая ставка цб
- Криптовалюты
- криптофонд
- Лондон
- лукойл
- Магнит
- майнеры
- машиностроение
- Медси
- Мечел
- Минфин
- ММВБ
- ММК
- МТС
- МТС-банк
- Нефть
- новичек
- ОГК-5
- ОИ в РИ
- ОМЗ
- опционные конструкции
- опционы
- открытый интерес
- ОФЗ
- ОФЗ-ПК
- оффтоп
- парный трейдинг
- Пенсионная реформа в России
- Петров
- президент
- продажа опционов
- Разгуляй
- Распадская
- РБК
- Ренова
- РЕПО
- Роснефть
- РТС
- Русснефть
- рынок ставок
- сбербанк
- Солсбери
- ставки на спорт
- страховка
- США
- ТГК-9
- технический анализ
- торговая стратегия
- торговля объёмами
- трежерис
- философия
- финансовый анализ
- фундамент
- фундаментал
- фундаментальный анализ
- фьючерсы на ОФЗ
- хеджер
- ЦБ
- ЦБ России
- ЧТПЗ
- Чуркин
- шпиль
- экономика
- экспирация
- эфириум






















