Избранное трейдера Dao Sun
НЕФТЬ.СОТы. Серия 1708."Всё расписано на пол года вперед."
- 02 августа 2017, 13:30
- |
и удивляюсь, что не предложение то всё в яблочко, ну прям Нострадамус в шляпе.
- позиции разгрузили за линию поддержки
- вниз упали на 10 баксов с 54 до 44
- хомяков по пути сквизанули
- и все шорты сложили в один месяц
- и месяц ближе к осени
Фонды резко набирают шорты. Понятно что когда то это приведет к их покрытию и резкому взлёту нефти. Знать бы какие контракты они шортят. Об этом можно только догадываться, по крайней мере нам простым спекулянтам. Я думаю что они шортят не Майский, а что нибудь подальше. В противном случае эти шорты придется крыть в Апреле и это был бы офигенный подарок хомякам, во что верится с трудом. Как говорил Матроскин, фотки шарика надо сдавать туда где платят больше. (Где контанго больше) А контанго больше ближе к осени.Лонги размазаны на много месяцев вперед, и их быстренько не закроешь, а вот шорты долбятся, очевидно, в какой то месяц, в котором и будет отскок. Вопрос в каком?
( Читать дальше )
- комментировать
- ★8
- Комментарии ( 27 )
Когда с нами занимаются сексом, которого мы не хотим, мы становимся сильнее и крепче
- 28 июля 2017, 15:32
- |
А сами в этом время не замечают, что их восьмилетний растущий тренд приказал долго жить.
Многие «работники отрасли», не торгующие, а читающие отчетики и аналитику таких же неторгующих, не осознают этого, однако мы с вами трейдеры, давайте просто посмотрим несколько графиков крупнейших американских компаний после вчерашнего отката (разметка финвиза, не моя).
1. Итак, АМАЗОН.

С 2016 года цена акции выросла двое. в 2017 году (рост пошел сразу с января) +40%. 2016 год — это прошлый год. Прибыль к прошлому году - как гласит годовой отчет — упала на 77%, пусть и при выросшей выручке. Отдельный липовый рост с июля под отчет.
Как мы видим, рост с 2016 года- пузырь.
( Читать дальше )
Когнитивные искажения мышления у трейдеров(все посты в одном)
- 10 июля 2017, 15:52
- |
http://smart-lab.ru/blog/400539.php
http://smart-lab.ru/blog/401351.php
http://smart-lab.ru/blog/404035.php
И добавить еще немного измышлений на этот счет.
Когнити́вные искаже́ния — систематические ошибки в мышлении или шаблонные отклонения, которые возникают на основе дисфункциональных убеждений, внедренных в когнитивные схемы, и легко обнаруживаются при анализе автоматических мыслей. Существование большинства когнитивных искажений было описано учёными, а многие были доказаны в психологических экспериментах.
Генерализация частных случаев — безосновательный перенос характеристик частных или даже единичных случаев на обширные их совокупности. Существует множество видов этого когнитивного искажения.
В трейдинге очень частое явление, выделение одного «сработавшего паттерна» и попытка наложить его принципы на любую рыночную ситуацию, совершенно не учитывая другие факторы, которые могут иметь намного большее влияние. Также это проявляется в поиске «кукловода» в каждом хвосте свечи, опять же обычно эти доводы не подкреплены даже реальными рыночными данными, например объёмами, то есть хвост свечи это обязательно срыв стопов «толпы», даже если реально в этом хвосте исполнилось «2 стопа».
( Читать дальше )
Управление стрессом
- 27 июня 2017, 11:56
- |
Всех приветствую.
Думаю для большинства участников рынка,а особенно для «домашних» трейдеров будет полезным решение данной задачи.
Я отдаю себе отчет, что на смартлабе очень разнообразная публика.
Однако надеюсь, что пост увидят в том числе и заинтересованные люди.
(сразу хочу заметить, что данный аспект торговли актуален только при наличии других,
не менее важных составляющих:
управления финансами, рисками, временем, торговой стратегии).
Итак: необходимо найти решение для управления стрессом.
В идеале — контроль над накопленным стрессом.
Можешь мотивировать и убеждать, но стресс ты не уберешь.
Хочу воедино собрать лучшие методики для контроля и управления уровнем стресса.
Именно в трейдинге. Не нужно мне «универсальных методов» на все случаи жизни.
Учесть психотипы. Учесть основные типы торговли.
Протестировать на реальной торговле (на себе и на контрольных группах).
( Читать дальше )
Вопрос по торговле облигациями
- 02 мая 2017, 16:36
- |
Сам ими никогда не торговал, но появилась необходимость в «безрисковой» стратегии с минимальной доходностью.
Цель-обгонять сберовский депозит высоколиквидными облигациями с максимально надежными эмитентами.
Господа подскажите как установить 2 квика от одного брокера на 1 компьютер.
- 22 декабря 2016, 15:21
- |
Исправления в "Алгоритмах маркетмейкера"
- 18 июня 2015, 13:48
- |
В цикле статей "Алгоритмы маркетмейкера" в пятой части был размещен мой код на C# для реализации стратегии оптимального управления ордерами. Пользователь сайта Eskalibur обнаружил в нем несколько ошибок, которые значительно влияли на результат, и доработал алгоритм до полного соответствия оригинальной статье. Его код я поместил в конце пятой части цикла статей (см. также комментарии к ней). Прошу всех, кто пробует применять эту стратегию, использовать именно этот листинг.
Хочу выразить благодарность за проделанную работы Eskaliburу и пользователю r0man, который также работает в направлении практического применения алгоритма. Думаю, у них все обязательно получится, и по результатам разместим отдельную статью на сайте.
Алгоритмы маркетмейкера. Часть 5
- 09 апреля 2015, 11:27
- |
Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора 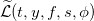 , в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью
, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью 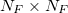 , где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
, где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
( Читать дальше )
Алгоритмы маркетмейкера. Часть 4
- 07 апреля 2015, 11:25
- |

Прошлые части цикла здесь. В этой части статьи мы найдем численное решение системы уравнений оптимального управления позицией маркетмейкера. Такое решение легко запрограммировать и использовать в реальной торговле для контроля за лимитными и маркет ордерами в соответствии с полученными стратегиями θmk,θtk. Для упрощения разложим функцию владения на слагаемые, чтобы получить сокращенную функцию владения v(t,y,f,s), которая представляет собой только динамическую составляющую основной функции:
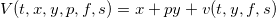
( Читать дальше )
Алгоритмы маркетмейкера. Часть 3
- 02 апреля 2015, 09:46
- |
Продолжаем разбирать работу JIANGMIN XU «Optimal Strategies of High Frequency Traders». Чтобы составить уравнение оптимального контроля, сначала сформулируем проблему оптимизации алгоритма при используемых стратегиях θ, как достижение максимума следующего матожидания:
![Алгоритмы маркетмейкера. Часть 3 \max_{\theta^{mk},\theta^{tk}}\mathbb{E}_0[X_T-\gamma\int^T_0 Y^2_{t-}d[P,P]_t]](http://mathurl.com/pthr6jr.png) ,
,
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал



