Подумал, что многие не знают, как подступиться к языку Qlua и запустить робота в квике. А между тем, это настолько просто, что даже не требует ничего кроме квика, виндусовского блокнота и знаний самого Qlua.

Qlua – это скриптовый язык поддерживаемый квиком, в основе язык lua 5.1 (в моем квике версия такая).

Скрипты, написанные на Qlua – это обычные текстовые файлы, которые имеют расширение «.lua». То есть можно сделать файл в обычном блокноте и после сохранения поменять в нем расширение с «.txt» на «.lua». Если внутрь этого файла записать инструкции кода на языке Qlua, то квик будет выполнять их.

Для удобства написания инструкций кода лучше пользоваться не виндусовым стандартным блокнотом, а например Notepad++, который можно скачать официально и бесплатно здесь https://notepad-plus-plus.org/download/v6.9.1.html. Он позволяет включить подсветку синтаксиса различных языков программирования, в том числе и lua, что очень помогает при написании кода.

В Notepad++ в «Опции -> Настройки» можно выбрать русский язык, а в «Опции -> Определение стиля» установить для lua понравившийся стиль отображения. Я для «Язык -> lua» ставлю стиль «Выбрать стиль -> Bespin» и еще в окошке «Стиль» для последних трех «FUNC» переопределяю цвет, иначе они с фоном сливаются.

( Читать дальше )

Картинка для затравки, Out of Sample perfomance (то есть результаты получены на выборке на которой не производилось построение модели):


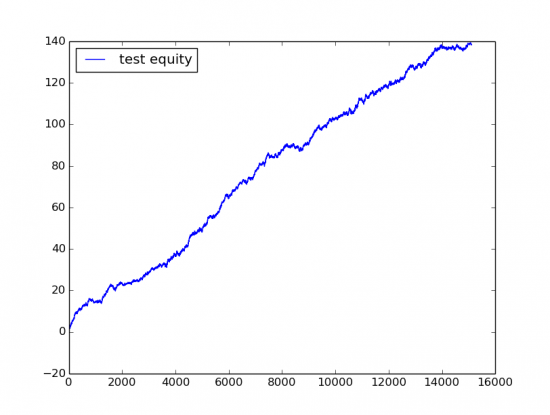
Сбербанк MOEX 15106 трейдов прибыль 140 руб на одну акцию, периодичность трейдов где-то 15 минут, equity где-то за год.
То же самое для Ri, 22237 трейдов прибыль 100000 пунктов на один контракт, или 5 пунктов на трейд, периодичность такая же 15 минут.

( Читать дальше )

Основы матричных вычислений, Уоткинс
Теория вероятностей, Вентцель
Теория случайных процессов, Панков и Миллер
Вероятность, Ширяев
Избранные труды, Колмогоров
Методы и техника обработки сигналов, Макс
Теория секвентного анализа, Хармут
Стохастические дифф. уравнения, Оксендаль
Цифровой спектральный анализ, Марпл
Справочник по броуновскому движению

Вступление

     Никогда не увлекался скоростным трейдингом. Всегда хватало терминала. Изучать этот протокол меня побудил набор вакансий. Надо отметить, что я неспешно перебираю хорошие вакансии на рынке. Частному трейдеру очень сложно развиваться в одиночку — психологически, эмоционально, физически. Создавать и развиваться постоянно хочется, поэтому принял решение вливаться в коллектив. За несколько месяцев, мне удалось провести несколько собеседований. На втором этапе я проваливался именно из за не знаний протокола.  Предметную область я примерно представлял. Ну что там сложного? Соединился с биржей по сокетам и начинай обмен сообщениями. Надо отметить, что в этой области есть уже готовые разработки в виде quickfix или готового API от StockSharp (правда платные). Но я принял решение разбираться с нуля, чтобы вникнуть в детали.

Технические аспекты протокола

     Итак. Любой протокол, какой бы он сложный не был, работает примерно одинаково. Мы создаем у себя соединение с сервером, устанавливаем некий туннель между нами и сервером, посредством которого будем обмениваться сообщениями. Протокол — это как раз и есть набор правил, по которым строятся сообщения нужного формата. Если говорить технически, то мы должны создать сокет соединение с сервером на указанный порт.
Сообщение в FIX, как и в любом другом протоколе, состоит из нескольких блоков:

• <Заголовок сообщения>
• <Сообщение>
• <Концовка сообщения>

     Наша задача, правильно заполнить эти блоки и отправить на сервер. Заголовок сообщения в свою очередь состоит из следующих данных:

• <Начало сообщения, версия протокола>
• <Длина (размер) сообщения>
• <Тип сообщения>
• <Идентификатор отправителя>
• <Идентификатор получателя>
• <Номер сообщения>
• <Время отправки>

     Обращу ваше внимание, что я перечисляю обязательные поля. Есть еще и дополнительные. Концовка сообщения должна выглядеть так:

• <Контрольная сумма сообщения>

     Сами данные заполняются достаточно легко. В виде: <тип поля> = <значение>. Например, <длина сообщения> = 78, то есть мы серверу говорим, что размер передаваемого нами сообщения составляет 78 байт. Стоит обратить внимание, что в протоколе FIX, типы полей кодируются в виде числовых значений. Например,  <длина сообщения> в протоколе передается как цифра 9. Исходя из выше сказанного, наш заголовок сообщения, выглядел бы следующим образом:

• 8=FIX.4.4 _____ начало сообщения, протокол версии 4.4
• 9=78 _____ размер сообщения 78 байт
• 35=A _____ тип сообщения А, что означает попытка на соединение с сервером
• 49=<ваш идентификатор выдается биржей>
• 56=FG _____ идентификатор получателя, раздел Forts на бирже
• 34=1 _____ первое сообщение
• 52=20160212-11:42:51.812 _____ время отправки сообщения

Организационные вопросы

1. Наша биржа дает тестовый контур для отработки своих алгоритмов по данному протоколу. Надо всего лишь написать запрос на доступ. Надо признать, тех служба работает отменно. Очень все быстро было организовано. Подробности http://moex.com/s442
2. Обязательно понадобится описание протокола для нашей биржи ftp://ftp.moex.com/pub/FIX/Spectra/test/docs/spectra_fixgate_ru.pdf
3. Чтобы вникнуть в тонкости передачи, мне очень помогла эта программа от биржи (позже я покажу как помогла) ftp://ftp.moex.com/pub/FIX/Spectra/Utils/fix_client.zip
4. Описание самого протокола от создателей (на английском). Мне помог сильно wiki. http://fixwiki.org/fixwiki/FIXwiki
5. Чтобы найти свои ошибки, мне приходилось перехватывать сообщения рабочего клиента биржи и сверять со своими. Для этого мне понадобился tcp/ip сниффер — программа перехвата сетевого трафика.
6. Разработку я веду на c#.

К бою. Немного теоретической практики

     На момент изучения протокола, я уверен, многие столкнуться со следующими вопросами:

• как именно считать длину сообщения
• как разделять между собой данные
• как считать контрольную сумму

     Если говорить образно. То, чтобы отправить сообщение на сервер, нам просто нужно сформировать нужную строку со всеми данными и отправить ее на биржу. Ну например:

8=FIX.4.4;9=78;35=A;49=FG;56=tgFhcfx901U05;34=1;52=20160212-11:42:51.812;98=0;108=3000;141=Y;10=047;

     Если быть внимательным, то мы увидим, что кол-во символов в строке у нас 100, а в заголовке сообщения мы передаем, что 78 (9 = 78). По правилам протокола FIX, длину сообщения нужно считать без учета концовки и первых двух полей заголовка. А именно:

     С длиной сообщения разобрались. Теперь про разделитель. Пока в моем скрине это ";". В документациях западных написано что это символ SOH. Чтобы однозначно ответить на этот вопрос, я запустил прилагаемого клиента биржи и сниффером стал перехватывать сообщения между клиентом и биржей. Кстати, программа ведет логи, и их общение выглядит так (зеленое — передача запроса на биржу, красное — ответ от биржи):

     Зачеркнул свой идентификатор, прошу понять правильно. Ну а перехват сообщения выглядит так:
     Зеленым я отметил именно разделители. Как вы уже видите, это просто в шестнадцатеричном виде код 01. То есть, в нашу строку в виде разделителей, нужно вставлять код 01. Также я отметил для себя последовательность полей в сообщении. Почему то в другом порядке у меня вызывало ошибки (возможно тут я не прав)
     Ну и контрольная сумма. Контрольная сумма считается над всем сообщением, за исключением концовки. То есть в расчет берется только заголовок и само сообщение. Для этого, мы переводим каждый символ в его Ascii код и вычисляем их сумму. Полученную сумму делим по модулю 256. Это и будет контрольной суммой сообщения. При этом, значение должно быть трехзначным. Если мы получаем 2 знака, то подставляем 0 слева (например, если контрольная сумма = 68, то должны передать значении 068).

К бою. Начало программирования

     В законченном виде, разработка будет составлять готовый класс, для работы с протоколом. Теперь начинаю строить его по кирпичикам. Для начала, я создал несколько классов:

• класс для работы с заголовками
• класс для работы с сообщением подключения к серверу (onLogon)
• класс для работы с концовкой

    Каждый класс включает в себя поля, которые передаются и некоторые методы для их обработки.
    Класс для работы с заголовками. Пока просто выглядит так: 


     Как видим, первый метод строит нужную строку из полей. Обратите внимание, там присутствует наш разделитель в виде спец символа \u0001. Второй метод вычисляет размер заголовка (чтобы потом высчитывать размер сообщения). Надо обратить внимание, что при передачи времени, миллисекунды должны указываться в трехзначном формате (даже если миллисекунды = 52, то передаем 052). Следующие классы строятся по аналогии.
Класс создания сообщения на подключение (инициализация сессии)

Класс создания концовки сообщения


Попробую привести код консольной программы для теста в виде цитаты. Картинки вставляются плохого качества. Подробно комментирую.

//Получаем ip сервера
IPAddress ipAddr = IPAddress.Parse(server);
IPEndPoint ipEndPoint = new IPEndPoint(ipAddr, port);
//Создаем заголовк
HeaderMessage msHeader = new HeaderMessage
{
BeginString = «FIX.4.4»,
MsgType = «A», //Тип сообщения на установку сессии
SenderCompID = "",
TargetCompID = «FG»,
MsgSeqNum = 1
};
//Создаем сообщение на подключение onLogon
LogonMessage msLogon = new LogonMessage
{
EncryptMethod = 0,
HeartBtInt = 3000,
ResetSeqNumFlag = true
};

//Вычисляем длину сообщения
msHeader.BodyLength = msHeader.GetHeaderSize() + msLogon.GetMessageSize();
//Создаем концовку сообщения
TrailerMessage msTrailer = new TrailerMessage(msHeader.ToString() + msLogon.ToString());

//Формируем полное готовое сообщение
string fullMessage = msHeader.ToString() + msLogon.ToString() + msTrailer.ToString();
Console.WriteLine(«Сообщение для отправки {0}»,fullMessage);

//Создаем сокет для подключения
sSender = new Socket(ipAddr.AddressFamily, SocketType.Stream, ProtocolType.Tcp);
//Подключаемся
sSender.Connect(ipEndPoint);
Console.WriteLine(«Сокет соединился с {0} », sSender.RemoteEndPoint.ToString());

byte[] msg = Encoding.UTF8.GetBytes(fullMessage);
//Отправляем сообщение
int bytesSent = sSender.Send(msg);
Console.WriteLine(«Отправил {0} байт», bytesSent.ToString());

//Получаем ответ от сервера
byte[] bytes = new byte[1024];
int bytesRec = 0;
bytesRec = sSender.Receive(bytes);
Console.WriteLine(«Ответ от сервера: {0}», Encoding.UTF8.GetString(bytes, 0, bytesRec));

Все таки приложу и в виде картинок. Так наглядней. Кликабельно.


В результате мы запросили у сервера подключение с нашим логином. И получили от него ответ.

По мере развития, буду продолжать с теоретической частью. Если модераторы перенесут в раздел «Алго», я не против.

Продолжение Изучаю FIX протокол с нуля. Рисуем и программируем дальше.

Окончание.Начало здесь.

Проверка эффективности индикаторов на реальных данных

В качестве проверки верности результатов на симуляционных данных мы использовали два реальных набора данных для исследования производительности индикаторов. Эти тесты требовали уровня 6 данных, для того, чтобы мы смогли точно воссоздать книгу заявок, отслеживая каждый лимитный ордер в моменты его поступления, изменения и удаления из очереди заявок, так же как и исполнение различных ордеров для точной реконструкции событий. В дополнение, мы присвоили каждому ордеру идентификатор, который классифицировал этот ордер как автоматический или ручной. Последней задачей был поиск событий, происходящих на отдельных рынках для изучения их влияния на происхождение мини обвалов цены.

Мы использовали два отдельных набора данных для исследования предсказательной способности индикаторов:

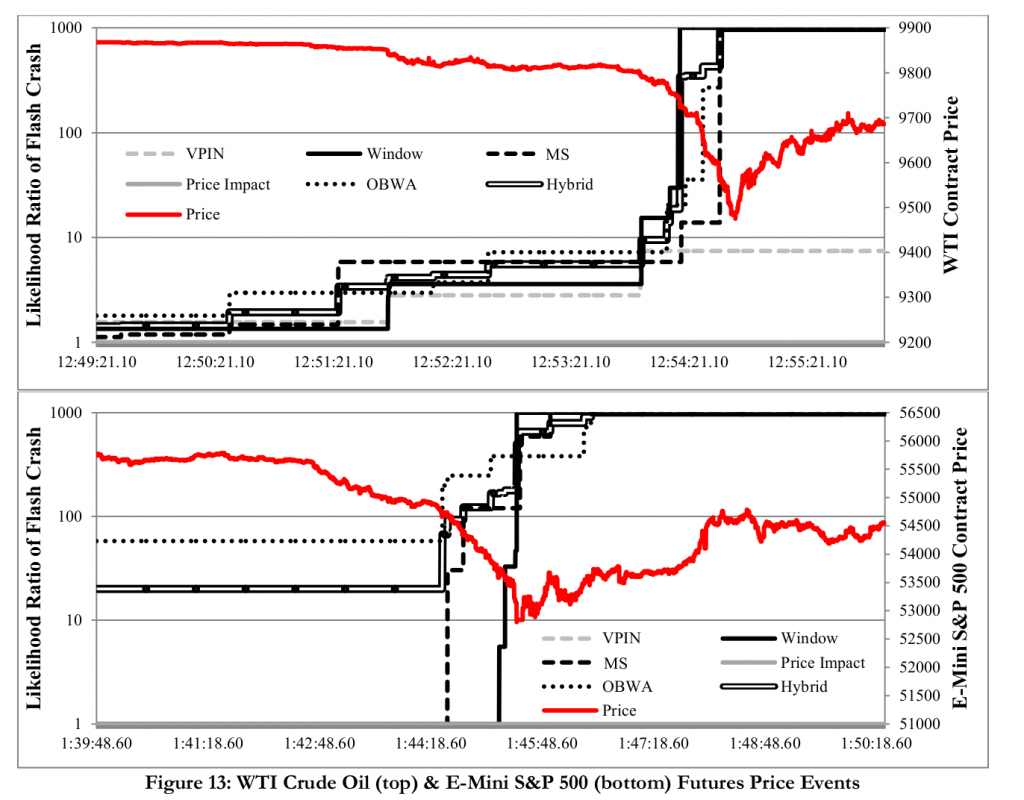
1. Сентябрь 19,2012. Падение фьючерсов WTI Crude Oil, когда цена снизилась более 4$ за четыре минуты ( большая часть падения была в интервале 30 сек этого периода), и достигла минимума в 12:55 дня.
2. Обвал цен 6 мая 2010. Обвал произошел на фьючерсах E-mini S&P500, когда цена упала на 3% за четыре минуты. В 1:45 дня она достигла минимума, когда биржа CME остановила торги (планка), затем цена начала свое восстановление.

( Читать дальше )

Написал бектестер на С++ для тестирования скальперских стратегий, с перспективой дописания его до рабочего робота. Вот только прибыльную стратегию родить так и не смог. Теперь вот не знаю, как поиметь какой-нибудь профит с разработки. Возможно заинтересованная общественность что-нибудь предложит.

Тут хочется сделать некоторое отступление и написать немножечко о С++. Здесь на сайте частенько попадаются сообщения в стиле «хочешь быстрого робота, пиши на плюсах!». Понятно что большинство здешних «программистов», советующих или критикующих С++, дальше lua (в лучшем случае C#) ничего не трогало, поэтому помимо высокой скорости работы программ, написанных на С++, единственное, что ещё упоминается, так это то, что писать программы на этом С++ безумно сложно. Отчасти это так, однако современный С++ (11-й и 14-й стандарты) — это (простите за тавтологию) современный язык программирования, который в выразтиельности программ может вполне потягаться с тем же С#.

Вобщем что может мой бектестер сейчас:

( Читать дальше )

         Любителям квантовой механики.

     Надо возвращать словам исконные значения. Приложил некоторые усилия, чтоб очистить термины “Фрактал” и ”Теория Хаоса” от от того, что навесил на них околорынок. Теперь дошла очередь и до “Квантовый трейдинг”. Виноват, до меня некоторые намеки доходят медленно, да и загружен был. Но дошло все-таки. Нашел время посмотреть.


( Читать дальше )

     Сейчас я попробую разложить торговлю по полочкам, вычленить независимые составляющие и их проанализировать.

     Пусть у нас есть торговый алгоритм, который выдает приказ на покупку или продажу. Для выхода используем тупой алгоритм типа таймаут, случайный выход, выхода по стоп-лосс, тейк-профит, трейлинг-стоп и т.п. Комиссию не учитываем.

     Обозначим рекомендацию алгоритма O[i] = -1, 0, 1, где i — номер потенциальной сделки. -1 соответствует рекомендации продать, 1 — купить, 0 — ничего не делать. Объем сделки обозначим V[i] >= 0.

     Результат сделки и при единичном объеме и при условии что только покупаем обозначим R[i]. Будем считать что на рынке на всем периоде торговли нет устойчивого тренда вверх т.е. стратегия “купил и держи” в среднем прибыли/убытка не приносит. Тогда матожидание (M) от произвольной сделки на покупку равно нулю M(R[i])=0.

     Итого, мы разделили торговлю на три независимые составляющие: 

( Читать дальше )

Расширенная форма оператора for

В расширенной форме оператора for для последовательного получения значений переменной цикла используется вызов итератора. Цикл завершается, когда итератор возвращает nil.

Примечание

Под итератором понимается любая конструкция, позволяющая перебирать элементы некоторого набора. При каждом обращении к итератору он возвращает очередной элемент набора. В Lua итераторы обычно реализуются в виде функций.

Расширенная форма оператора for имеет следующий вид:

for var1, var2, …, varN in <explist> do

… — тело цикла

end

где:

var1, var2, ..., varN — список переменных, получающих значения на каждом шаге цикла. Список может состоять из одной или нескольких переменных, разделённых запятыми. Первую в списке переменную называют управляющей переменной цикла. Когда эта переменная получает возвращённое итератором значение nil, цикл завершается. Остальные переменные на ход выполнения цикла влияния не оказывают;

<explist> — список выражений, разделённых запятыми. Обычно список состоит из единственного выражения — вызова функции-фабрики итераторов. Такая функция возвращает функцию-итератор, состояние и начальное значение управляющей переменной цикла.

( Читать дальше )

Скрипты на языке Lua

Написанный на Lua скрипт не имеет какой-либо специальной функции, с которой начиналось бы его выполнение. Скрипт можно рассматривать просто как набор команд (инструкций), который выполняется, начиная с первой инструкции.

Скрипт может быть как очень простым, состоящим всего из одной команды, так и весьма сложным, содержащим десятки, сотни и даже тысячи инструкций. Следующие друг за другом инструкции могут разделяться точкой с запятой (;). Однако это требование не является обязательным, поэтому весь приведённый ниже код является корректным с точки зрения синтаксиса:

a = 1; b = 2

a = 1 b = 2

a = 1;

b = 2;

a = 1

b = 2

Работа с переменными в Lua

Переменные используются для хранения значений в процессе выполнения скрипта.

Имена переменных в Lua

Именами (идентификаторами) переменных в Lua могут быть любые последовательности из букв, цифр и символа подчеркивания, начинающиеся не с цифры.

( Читать дальше )