Избранное трейдера Oblitus
Очень классная книга! Александр Силаев - Деньги без дураков.
- 17 ноября 2019, 20:40
- |

Однозначно советую всем! Причем даже опытным. И вот почему.
Эта книга — тот редкий случай, когда книгу про инвестиции/трейдинг мне читать еще интересно. Мне кажется, я уже знаю почти все, поэтому меня сложно чем-то удивить, это надо учитывать, когда вы читаете рецензию от меня.
Сразу оговорюсь, что в целом, книга произвела неоднозначное впечатление: вначале она прям меня привела в чувство полного восторга. С половины книги, я “увяз”, уже не мог читать, пролистывал страницы. Но новичкам — однозначно читать вдумчиво и целиком. Лично для меня было бы идеально, если бы она закончилась на половине. Но это чисто для меня. Теперь по делу.
Автор книги, Силаев — большой молодец, я проникся уважением к его интеллекту, эрудиции, кругозору и дару писать. Начало книги я вообще читал взахлеб, оставил массу пометок на страницах. Я бы даже сказал, что он пишет не хуже Талеба. Итак, автор:
оригинально мыслит и пишет
необычный текст и слог
я читал и получал удовольствие от чтения.
Только есть проблема. Некоторые места книги настолько оригинальны, что не все это поймут и оценят. По-моему я не встретил в книге ни одного момента, где я был бы не согласен с автором. Более того, многие моменты мне близки именно с позиции моего опыта и я рад что увидел в этой книге похожие мысли.
Какие интересные идеи я бы подчеркнул?
(Мысли очень концентрированные, на самом деле далеко не все поймут и осознают сходу их ценность)
( Читать дальше )
- комментировать
- ★43
- Комментарии ( 86 )
★Риск менеджмент в трейдинге: лучшие книги для начала!
- 04 ноября 2019, 17:35
- |
«Биржевая книга. Сделай миллионы, играя числами» (автор – Райан Джонс)
Пожалуй, это единственный автор, который рассматривает риск-менеджмент не только как торговую стратегию, которая мало кому понятна поначалу. Райан знаменит тем, что привык объяснять особо сложные понятия простым и доступным языком.
скачать книгу
.
Книги — «Математика управления капиталом» (Р. Винс) и «Новый подход к управлению капиталом»
Они позволят вам по другому взглянуть на трейдинг. Его методика основана на простой математике. Только цифры, и ничего более!
скачать книги
.
«Энциклопедия финансового риск-менеджмента» (авторы — А. А. Лобанова, А. В. Чугунова)
Данное пособие является первым учебником, выпущенном на русском языке, в котором риск-менеджмент рассматривается как наука, в которой, прежде всего, необходимо большое внимание уделять дисциплине и тщательному анализу.
скачать книгу
( Читать дальше )
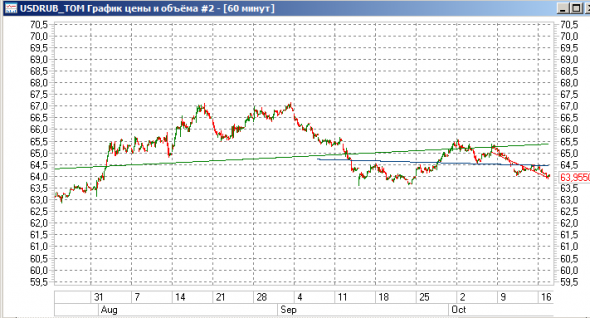
Индикатор, показывающий тренд
- 17 октября 2019, 15:36
- |
работать с ним нужно так:
если цена ниже линии, то перепроданность — нужно покупать, если сверху, то перекупленность — продавать
можно построить несколько трендов за разные периоды и делать покупки тогда, когда сигналы совпадают
PS:
кидайте тимофейчики
Settings={
Name="MNK",
period=200,
line=
{
{
Name = "cur1",
Type =TYPE_LINE,
Width = 1,
Color = RGB(255,0, 0)
}
}
}
--[[
описание свойств:
period - период, за каротрый делается расчет
назначение:
построение тенденции
использовался:
метод наименьших квадратов (аппроксимация линией)
--]]
function Init()
return 1
end
function OnCalculate(index)
sz = Size()
n = Settings.period
if (index ~= sz) then
return nil
else
y = nil
if index-n > 0 then
a1 = 0
a2 = 0
a3 = 0
a4 = 0
for i=index-n+1, index do
a1 = a1+i*C(i)
a2 = a2+i
a3 = a3+C(i)
a4 = a4+i*i
end
if((n*a4 - a2*a2) ~= 0) then
a = (n*a1 - a2*a3)/(n*a4 - a2*a2)
b = (a3 - a*a2)/n
for j=index-n+1, index do
y = a*j + b
SetValue(j, 1, y)
end
end
end
return y
end
endЧестная книга о том, как добиться успеха.
- 10 сентября 2019, 18:24
- |
Главы:
1. Никто не знает, как правильно.
2. Люди добившиеся успеха не знают, как повторить успех.
3. Невероятный карьерный рост у отдельных людей — это просто статистическая закономерность.
4. Учёные неоднократно доказали, что свободы выбора нет. От ваших решений ничего не зависит.
5. Вы технически не можете быть счастливы чаще, чем счастливы сейчас.
6. Любая жизнь — жопа.
7. Если вы что-то будете делать, то что-то будет меняться.
8. Не научились в детстве — теперь научиться гораздо сложнее.
9. Если у кого-то получилось — это не значит, что получится у вас.
10. Вы конкурируете за ресурс с миллиардами людей.
11. Эта книга написана, чтобы автору конкурировать было проще.
12. Чисто статистически вы не тот, кто добьётся значимого успеха.
13. Бога нет, рая нет, ад есть, вы в нём.
14. Работать в найме — это бессмысленный ад.
15. Предпринимательство — это бесконечный ад.
16. Деньги никого не сделали счастливым.
17. Путешествия никого не сделали счастливым.
( Читать дальше )
Оформляем возврат на ИИС в 2019 году через личный кабинет сайта nalog.ru
- 14 января 2019, 16:49
- |
Итак по по порядку:
1) Заходим в личный кабинет на сайт nalog.ru, через: либо подтвержденную запись на госуслугах, либо через учетную запись полученную именно в налоговой службе.
2) Выбираем «Заполнить декларацию онлайн».

( Читать дальше )
Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год!
- 17 октября 2018, 13:53
- |
Теперь новая напасть. Как владелец иис, я возвращаю 52 000 рублей каждый год по ндфл. Делается это достаточно просто (по идее, и в этом году решили сделать ещё проще вроде как. в прошлом такой проблемы не возникало):
1.Вы сдаете декларацию 3-НДФЛ через тот же личный кабинет.
2.Она проходит камеральную проверку, и налоговый орган выдает решение о возврате (смотри скрин 1).

( Читать дальше )
Книга Technical Analysis на русском
- 16 октября 2018, 14:04
- |
Минимум воды, максимум рабочих ситуаций. Рекомендую к чтению! Реальная практика.
Cкачать в PDF тут Tekhnicheskiy_analiz_shenon.pdf

Как стать маркетмейкером на bitmex.
- 07 июня 2018, 14:50
- |
Само ПО находиться по ссылке https://github.com/BitMEX/sample-market-maker
Для тех, кто не знаком с Python рассказываю пошаговую инструкцию.

1. Заходим на https://www.python.org/ и скачиваем последнюю версию Python 3.6.4
( Читать дальше )
Алгоритмы для жизни: Простые способы принимать верные решения. Брайан Кристиан. Конспект книги: Часть 3
- 23 января 2018, 11:04
- |

Когда парковаться
Шоуп прославился благодаря своей книге «Высокая цена бесплатной парковки». Идеальное парковочное место, в понимании Шоупа, – то, в котором умело соблюден точный баланс между стоимостью места парковки, неудобством от ходьбы пешком, временем, затраченным на поиски свободного пространства.
Поиски парковки всегда включают в себя элемент теории игр: пока вы пытаетесь перехитрить всех водителей на дороге, они, в свою очередь, пытаются перехитрить вас[5]. Таким образом, большинство проблем с парковкой сводится к одному фактору – уровню заполненности. Это отношение общего числа парковочных мест к количеству занятых в данный момент.
Решение Шоупа предполагает
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал


