Вы наверное в курсе, что в результате активной борьбы с уходом от уплаты налогов, нал сильно подорожал. Схемы обнала последовательно прикрывают. В результате рождаются новые схемы.

Мне говорили, что сейчас очень активно используется схема продажи нала розничными интернет-магазинами. Те, которые через яндекс-маркет продают айфоны по-дешевке за нал с доставкой на дом. Продали айфон, получили нал, нал собрали, отгрузили, получили платеж на счет через фирму-однодневку, наварили еще процентов 10 после всех расходов. Ну а цена кэша поднялась до 15-17%. 

Ъ пишет, что в 2017 доля продажи выручки составила 29% транзитных операций. 

Я столкнулся с тем, что мне, честному ИП банк Авангард повысил комиссию за перевод на счет физического лица. Я уже писал об этом, что у Тинька например «штраф» может составить 15% от суммы, если ты выводишь >10 млн в мес. Говорят ЦБ сказал банкам так:

Кэш стал товаром. Банки, нам пох как, надо сократить объем транзита. Действуйте. 

Вот банки заодно начали грабить и честных предпринимателей, в том числе меня.  Говорят, что кэш покупается через фирмы-однодневки (транзитные). И ЦБ начинает давить на банки, а больше всего от этого могут пострадать банки, обслуживающие МСП (мал-сред-предприн).

Так вот чтобы прикрыть обнал через розничную торговлю, ЦБ разослал банкам инструкции, как выявлять и блокировать счета однодневок:

• 133 кодов ОКВЭД попали в «зону подозрительности» (точного списка нет)
• контора зарегистрирована после 1.1.2016
• счет в банке открыт после 1.1.2017
• налоговая нагрузка не выше 2%
• поступление и списание сумм выше 1 млн руб в качестве оплаты за авто и запчасти, табак, продукты и другие товары.

А еще ЦБ будет выявлять целые банки, через которых идет транзит, и отзывать лицензии.

Банкиры отметили, что, начиная с итогов IV квартала 2018 года, ЦБ будет учитывать объем описанных выше транзитных операций при определении общего объема сомнительных транзакций в банке. О высокой вовлеченности банка в противоправную деятельность будет говорить доля выше 2% от дебетовых оборотов по клиентским счетам или сумма от 1 млрд руб. за квартал, что может служить основанием для отзыва лицензии.

Народ, кто в теме — объясните смысл этой фразы? Я так понял, что ЦБ будет выявлять операции по 5 пунктам выше, и смотреть, если доля таких оборотов больше 2% от оборотов или >1млрд руб, то банку п**ц.

ну и главный вопрос: через банк QIWI идет огромный объем платежей с розничной торговли, и на банковском рынке говорят, что много обнала идет именно через инфраструктуру Киви. Как бы Цб не грохнул-то их лицензию под шумок:))

Что думаете?

( Читать дальше )

Часть 3-в. Надеюсь, предпоследняя.)))

 

    Вопрос, который не прозвучал в предыдущей части статьи – а где здесь неэффективность? Поскольку была «договоренность» называть неэффективностью информационную неэффективность, то в примере с бруском она заключается в том, что не все участники ставок на начало скольжения обладают полной информацией о системе, а получив ее, не одновременно реагируют. (возвращаясь к антиномии первой части: «Это значит принять решение о своей позиции на основе информации, которая не  доступна большинству, при том, что большинство имеет к ней доступ.»)

                                                 

    То есть, представим себе ситуацию, что очередной «заезд» начался, и несколько игроков с одинаковым объемом информации о системе (например, все они знают точно массу бруска, материал из которого сделан он и плоскость поверхности),  получают прямо в ходе «заезда» вводную информацию о качестве обработки плоскости скольжения. Кто сделает наиболее точное предположение о моменте начала скольжения? Очевидно, тот, кто быстрее и правильнее встроит эту новую информацию в формулу расчета искомого угла наклона. Это, опять же, и есть та самая неэффективность, определение которой было дано в первой части: «Рыночная неэффективность это свойство рынка, при котором время поступления информации меньше времени отклика на информацию».

( Читать дальше )

ТСЛАБ+IB опыт торговли америки

 

Давненько не писал. Много работал.

 

0 Пишу про акции. Фьючи дороже. Там нужен счет от ляма грина и выше. В техническом плане связка Тслаб+IB весьма стабильна. Напрягает сильно 13-14ти часовой рабочий день с 10 утра до 23-24 ночи без праздников.

 

1 В марте 2017г появилась возможность протестить америку при помощи связки тслаб2+IQfeed. Что позволяло выйти на алготорговлю на америке. Где то к августу сформировалась общая картинка. В мае 2018 закинул 74000 баксов. И где то в конце июля стал торговать роботами под америку на связке тслаб2+ IB через TWS. Приоиграл -10к баксов из них где то больше половины на багах и глюках. Наработал опыт. Делюсь.

 

2 Сразу скажу что по деньгам это дорого и затратно. Тслаб 4000руб в месяц + IQfeed 7000руб + выделенный сервер в датацентре 5000 в месяц + 1500 расходы на IB. Чтоб просто посмотреть и торговать надо иметь расход в районе -18000 в месяц или -210к в год. Дорого вкрай. Чтоб расходы были хотяб на уровне <5% в год размер размер счета должен быть более  4мио руб.

( Читать дальше )

Общеизвестный факт:

 Пример парадокса: если береговая линия Великобританииизмеряется отрезками по 100 км, то её длина составляет примерно 2 800 км. Если используются отрезки по 50 км, то длина равна приблизительно 3 400 км, что на 600 км больше.  

Парадокс береговой линии — противоречивое наблюдение в географических науках, связанное с невозможностью точно определить длину линии побережья из-за её фракталоподобных свойств. Первое задокументированное описание данного феномена было сделано Льюисом Ричардсоном

( Читать дальше )

Я тут недавно постил свою методику заработка пенсионных баллов на онлайн-проектах, как трейдеру не остаться без пенсии после слива депозита. У людей в комментариях были вопросы по сайтам, и как я на них зарабатываю. Я сделал вывод, что многим интересна тема инвестиций в сайты и заработка на сайтах.

Могу кратенько спалить немного инфы о своем основном текущем интернет-проекте и заработке с него. Трейдерам будет полезно (все равно торчишь у монитора, сливаешь, хоть бы что полезное сделал). Стебусь, конечно. Ну а если серьезно, сайты позволяют серьезно диверсифицировать доходы и снизить личные финансовые риски в рамках трейдерского лайфстайла (кровать-монитор-кровать — вы же не про Майами, тачки и телок сейчас подумали?)

Как заработать на своем сайте

Начну с вводной для тех, кто в танке. В интернете есть миллионы и миллионы сайтов. Глобально они делятся на 2 типа. Половина из них что-то продает, половина ничего не продает. Те, которые ничего не продают, называются

( Читать дальше )

Тут народ говорит, что надо писать громкие эмоциональные заголовки, чтобы сразу лайкалось:) ахаха
Всем доброго вечера, коллеги спекулянты и инвесторы! Мною замечено, что по мере погружения бумаг, социальная активность инвесторов на смартлабе снижается, и на первый план выходят краткосрочные спекулянты. 

Рынок наш по индексу вроде неглубоко ушел, но многие акции уже упали ниже плинтуса. Куча ликвидных бумаг в солидном минусе:
 
(ссылка на табличку) 

Мне в этом году везет и я думаю не просто так. Самое главное — я не вляпался во всякий падающий шлак из этой таблички. Сочетание фундаментала по акциям и чисто технический спекулятивный подход дали мне неплохой результат. Да, я пока немнго «угараю» на QIWI (купил высоковато), и стагнирую (но не падаю) на AGRO. Зато все позиции, которые уже закрыл, дали солидный плюс (USDRUB↑ , RASP↑ , GAZP↑ , SBER↓, S&P500↓ ). Некоторые позиции были закрыты до того, как успели сильно упасть (MOEX, PHOR) именно потому что я понимаю, что эти бумаги стоят на высоких мультипликаторах, и «маржа безопасности» там небольшая.

Что я думаю о текущем моменте? Хо-хо, товарищи, кто читает нашу стратегию на mozgovik.com в курсе, что я жду рецессию в США в 2019 году, поэтому считаю, что долгосрочные инвесторы в любом случае получат удар. Кроме того, серьезные опасения у меня вызывает Китай. В этом плане я жду что проблемы экономики могут транслироваться в проблемы на сырьевом рынке, а сильнее всех пострадают циклические компании, а акции металлургов сильно припадут в 2019. Но это лишь моя гипотеза «в работе». Я еще в апреле написал, что долгосрочные покупки надо делать на выходе из рецессии, а не на входе в нее (на пике экономического цикла), поэтому считаю, что долгосрочные инвестиции сейчас не особо удачная идея. 


( Читать дальше )

Написано было мною несколько лет назад:

Как то много лет назад, ещё работая брокером, звоню я наугад какому-то, по мои калькуляциям небедному, чуваку из телефонной книги (cold calling) и предлагаю ему купить какую-то акцию, которая, исходя из моего анализа, была перспективна. 

чувак мне говорит, но ведь это $30,000, а если вы ошибаетесь ?
почему я должен вам верить? вы сами купили эту акцию, вы сделали на ней деньги и на других таких же? если да то почему до сих пор звоните таким как я, если нет — то почему я вам должен верить ?

потом мы мило поговорили, и в общем понравились друг другу

но после его слов я глубоко задумался и начался у меня с самим собою разговор:

Саша, спросил я себя, какого хера  ты звонишь людям, ты знаешь как вкладывать куда, когда и сколько? ну так действительно вложи уже сам, пидор !

— Я не знаю как вкладывать, и на самом деле ссу сам вложить и ссу расплатиться за последствия, да и денег- то великих нет рискнуть — сказал я себе...

— Тогда зачем звонишь людям, ведь ж они просрут месте с тобой?..

( Читать дальше )

Как все, наверное, уже сегодня верно подметили, фьючи FORTS — это кухня и правит балом местный пакостник-кукловод!



«Торговать нужно со стопами» - это прописные истины...

Все так, без стопов никуда, но как их ставить то эти стопы, чтобы кукловод их постоянно не сшибал?

Кто давно в нашем болотце торгует, тот помнит такие же сопли во фьючах Gold. Но что там Gold, когда уже куклу всяких там неликвидов мало и он начинает зариться на самое ценное, что есть у российских спекулей в последнее время — фьюч Br!

Ответ прост: не будь плотвой, торгуй опционы!



( Читать дальше )

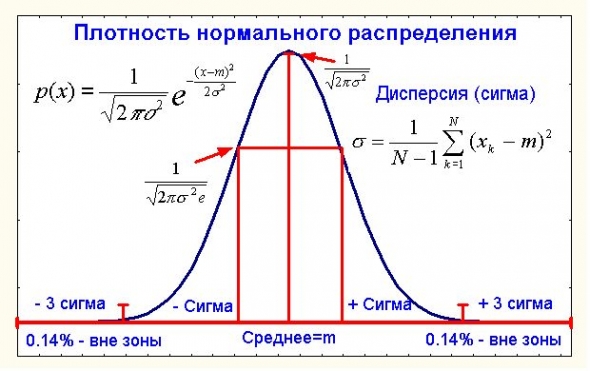
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

Давно известно, что если вы хотите купить какую-то акцию дешевле — продайте на нее пут не в деньгах. Например хотите сбер по 180? Продайте 180й пут. Если цена упадет ниже 180 — то вы получите акцию по 180 и еще премию по путу. (например 2) и таким образом эффективная цена покупки будет 178. Ну, а если цена не упала — то получите просто истекшую премию в размере 2, что в пересчете на ГО довольно неплохая доходность. Пример выше — условный, надо смотреть на цены, страйки, волатильность. Но есть одно простое правило — путы лучше продавать тогда, когда рынок уже припал и вола подскочила и часть падения уже пройдена. (Так, сейчас кто-то бросится писать коммент про мой 2008й год. Да, такое бывает. Но сейчас этих предпосылок, вроде как, нет).
Чем еще хорошо продавать путы? что если акция болтается в диапазоне, то вы собираете премию. Обычный владелец стока при неизменной (почти) цене акции получит лишь дивиденды, а вы — опционную премию. (правда не будет дивидендов)

Но тут возникает два момента — первый, с опционами не все знакомы и не все связываются и второй — не на каждый инструмент есть опцион. Поэтому сейчас я расскажу стратегию торговли, для которой не нужны опционы, но суть ее особо не поменяется. Более того, добавятся дивиденды.

( Читать дальше )