Корреляционная кластерная карта Российского рынка акций с начала 2017 года.

(в помощь ищущим чем бы задиверсифицироваться)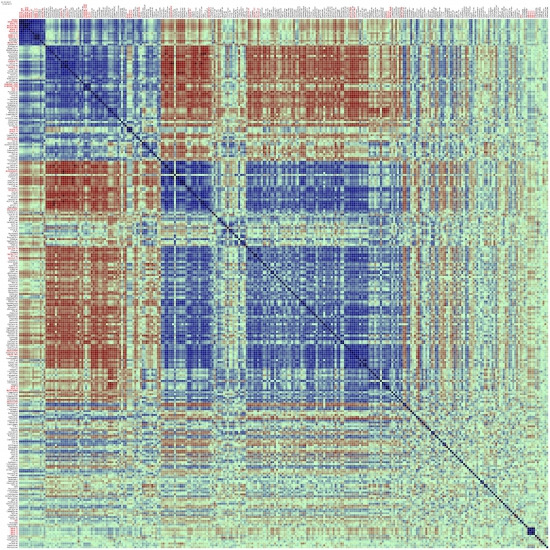




( Читать дальше )

Портировал из LUA в машинный код, один из любимых рабочих инструментов.

Аццкая смесь Homoscedasticity, Fractal dimension и некоторых «секретных ингредиентов» Probability theory, породившая приемлемый Support and Resistance, не зависящий от субъективности и настроений «прокладки» между рынком и кошельком.

Пока была в LUA больше 3-4 запустить не получалось, не «повесив» QUIK, а сейчас:



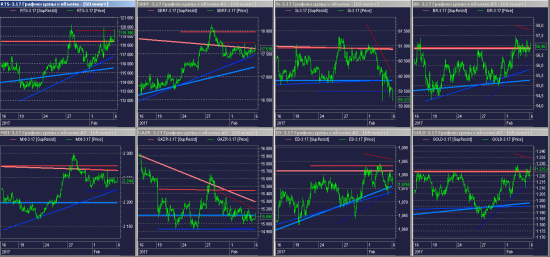
( Читать дальше )

Про улыбку только ленивый не говорил. Ну и мы лениться не станем.  Что бы пощупать улыбку своими руками вам надо. Пойти в туалет и не снимая штаны помыть руки, что бы потом включить эксель-калькулятор и скачать файлик

cloud.mail.ru/public/H7RV/k4MBtngy1

Дальше, ума много не надо. Из пакета «анализ данных» мы делаем «описательную статистику» и гистограмму распределения. (желтая заливка). Ручками, помытыми с мылом, ищем сигмы и строим нормальное распределение (зеленое). И начинаем все это сравнивать. Если от одного распределения отнять другое, то и получится улыбка или насколько наше распределение БА не совпадает с нормальным Гаусинским распределением.  Так как данных мы брали много, но не очень то мы получим некоторые точки, и если построить точечный график и выбрать макет с линией, то вы построите, только не пугайтесь, регрессию по наименьшим квадратам. Можно через функцию в каРкуляторе-эксель «тенденция» сделать то же самое. Ну, в общем, то и все. Берем 3 сигмы, считаем цену страйков и можем присваивать им полученную волатильность. Как видно улыбка СИ с задранным правым краем, у РИ наоборот. Видно чем это обусловлено. Реальные распределения сдвинуты. Правда, наша улыбка получилась не такой красивой, но это мы поправим. И теперь, той части аудитории, которой все ясно, можно вернуться туда, где они руки мыли, а мы продолжим.

( Читать дальше )

Под катом скучное и неинтересное описание устройства торговой программы.

( Читать дальше )

Для грамотных математиков любящих графики случайного блуждания, распределения приращений и кибернетикам с априорными гипотезами без доказательств.

Сжатие данных - алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого ими объёма, за счет устранения избыточности, содержащейся в исходных данных — повторяющихся последовательностей и значений.

Случайные сигналы, процессы, последовательности, белый шум не обладают свойством избыточности. Сжатие данных принципиально невозможно без потерь.

Гипотеза — если колебания цен есть случайный процесс то сжатие данных последовательности приращений не возможно и коэффициент сжатия не должен превышать 1. 

Условия испытаний. 

( Читать дальше )

Вспомогательная разметка линейными трендами дней и часов



( Читать дальше )

Такого у Вас точно Нет.
И Вы точно не пропустите рост объемов!



( Читать дальше )

Упрощенный алгоритм вычисления приближенного значения размерности Минковского, для ценового ряда.

Краткая справка:

Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:

• где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.

Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов. 

( Читать дальше )

ЗАВТРА В БОЙ!!!

А многие молодые квикеры-бойцы до сих пор пользуются стандартными индикаторами, машками, болинджерами и параболиками, а некоторые и вообще ничем не пользуются.

И в глазах опытных «охотников» за депозитами:



экипировка молодого бойца выглядят так:


( Читать дальше )

Индекс относительной силы (RSI от англ. relative strength index) — индикатор технического анализа, определяющий силутренда и вероятность его смены. Популярность RSI обусловлена простотой его интерпретации. Индикатор может рисовать фигуры технического анализа — «голова-плечи», «вершина» и другие, которые часто анализируют наравне с графиком цены

Каждый трейдер в своей жизни проходил через данный индикатор, были и сигналы, и «вроде как дивергенция», и перекупленность с перепроданностью на глазок

Но стандартно встроенная реализация RSI не позволяет сделать и малой части.

( Читать дальше )