Избранное трейдера Шторм
Что нужно, чтобы зарабатывать на рынке (по мотивам ТА фуфло)
- 16 декабря 2016, 12:38
- |
Сначала хотелось вставить свою копеечку по поводу ТА, но потом я передумал. И понял, что весь сыр бор собственно из ничего.
Тимофей связал заработок с использованием анализа. Как по мне, так смотреть нужно совсем на иные вещи. Немножко подумав, я набросал основные и гораздо более важные вещи на мой взгляд.
Итак, в чем разница между людьми, которые зарабатывают на рынке. Смотрим!
( Читать дальше )
- комментировать
- ★12
- Комментарии ( 11 )
Сканер рынка для QUIK
- 01 декабря 2016, 13:01
- |
В терминале QUIK доступны сотни и даже тысячи инструментов. Как найти среди них те, в которых выполняются определённые условия? Например, бумага начала расти или достигнут локальный минимум и имеет смысл рассмотреть вопрос покупки этого актива? Или какое-то другое условие, которым пользуетесь именно вы для анализа ценных бумаг рынка.
Очевидный путь — листать эти инструменты в терминале. Да, можно. Например, просматривать дневные графики всех инструментов на сон грядущий вместо сказки на ночь. Или проводить все время перед экраном, тренируя мышцы руки, истирая мышку и ломая глаза, если интересуют сигналы для торговли внутри дня. Даже не принимая во внимание трудоёмкость и малоприятность процесса, часть сигналов в любом случае будет пропущена.
Однако процесс поддаётся автоматизации — и это хорошо. Я не встречал в открытом доступе подобных утилит, поэтому некоторое время назад написал такую утилиту для себя. Она оказалась удобной — я ее причесал и делюсь с публикой. Лишний плюсик в личное дело на главном суде не помешает.
( Читать дальше )
Трейдеры, любите каналы!
- 03 ноября 2016, 22:25
- |
Нужно торговать ПРОБИТИЕ канала. Когда произошло пробитие, надо подождать второго события — возврата к линии канала. Теперь она является сопротивлением. И только после этого нужно шортить. То есть стратегия состоит из 4 шагов.
1. Цена болтается в канале. Ждём, не торгуем.
( Читать дальше )
Индикатор фрактальной размерности | LUA
- 07 октября 2016, 15:50
- |
Упрощенный алгоритм вычисления приближенного значения размерности Минковского, для ценового ряда.
Краткая справка:
Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов.
- где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.
( Читать дальше )
Доклад «Оптимизация портфеля алгоритмических стратегий» на конфе смартлаба 24.09.16
- 30 сентября 2016, 12:00
- |
Доклад «Оптимизация портфеля алгоритмических стратегий»
1. Введение
В чем состоит цель подобной оптимизации? Представим, что у нас есть набор алгоритмов, каждый из которых обладает некоторыми статистическими свойствами, из которых наиболее важными для нас являются доходность и максимальная величина просадки. В основе каждого из алгоритмов лежат разные стратегии, которые, тем не менее, могут быть коррелированы между собой в разной степени, торговля также может вестись на разных инструментах. В качестве примера приведу характеристики стратегий, которые были разработаны нашей командой и применяются в боевых торгах в настоящее время:
Так как свойства каждого из алгоритмов отличаются, возникает проблема: каким образом распределить между ними доступный капитал для того чтобы:
1. Максимизировать доход при заданном уровне риска ( то есть максимальной величине просадки)
2. Минимизировать риск при заданной доходности
Если дать, например равные доли капитала каждому алгоритму, то, очевидно, что такое распределение не будет оптимальным, так как мы не учитываем характеристики, присущие стратегиям. Не будет оптимальным и тот случай, когда мы, например, выделяем капитал пропорционально относительной доходности каждого алгоритма, здесь мы игнорируем значения волатильности, то есть риска, стратегий.
2. Модель Марковица
Задачу оптимизации попробуем решить, применив теорию оптимального портфеля, разработанную Марковицем, точнее некоторые последующие ее модификации. Обычно данная теория применяется для долгосрочного инвестиционного портфеля, состоящего из различных активов, например акций. Кратко суть теории.
( Читать дальше )
ЛЧИ 2016 - экипировка для выживания молодого бойца (QUIK LUA)
- 14 сентября 2016, 12:12
- |
ЗАВТРА В БОЙ!!!
А многие молодые квикеры-бойцы до сих пор пользуются стандартными индикаторами, машками, болинджерами и параболиками, а некоторые и вообще ничем не пользуются.И в глазах опытных «охотников» за депозитами:

экипировка молодого бойца выглядят так:

( Читать дальше )
Памятка по ликвидности в FORTS
- 01 сентября 2016, 12:12
- |
Памятка о том где лежат деньги, и где ликвидность на нашем срочном рынке
Топ 10 инструментов «Где лежат деньги» (31/08/16)
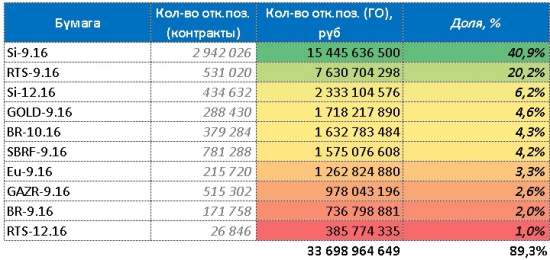
( Читать дальше )
Негативная аномалия в рубле
- 30 августа 2016, 21:39
- |
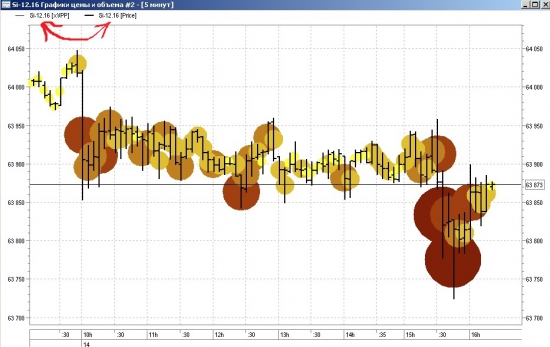
Вроде бы никаких предпосылок и нефть на максимумах, но при регрессии USD/RUB через нефть — уровень должен быть порядка 64 при фактических 65,2 (1,2 рубля или ~ 1,8%) на сегодняшний день.
При этом данная бэквордация (или контанго (кому как удобно)) планомерно нарастает.
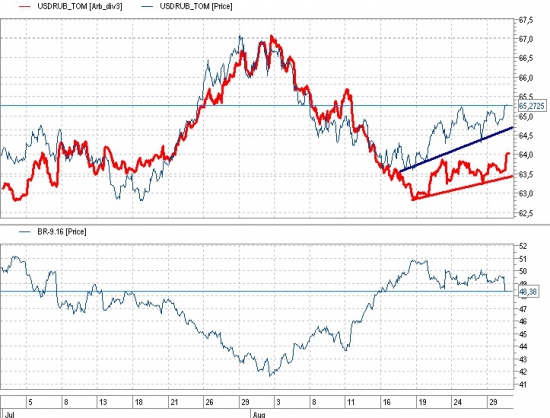
( Читать дальше )
RSI альтернативные возможности и нестандартное использование (LUA)
- 03 августа 2016, 14:36
- |
Индекс относительной силы (RSI от англ. relative strength index) — индикатор технического анализа, определяющий силутренда и вероятность его смены. Популярность RSI обусловлена простотой его интерпретации. Индикатор может рисовать фигуры технического анализа — «голова-плечи», «вершина» и другие, которые часто анализируют наравне с графиком цены
Каждый трейдер в своей жизни проходил через данный индикатор, были и сигналы, и «вроде как дивергенция», и перекупленность с перепроданностью на глазок
Но стандартно встроенная реализация RSI не позволяет сделать и малой части.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал