Машинное обучение

После рассмотрения основ машинного обучения в первой части, мы перейдем к примеру использования наивного байесовского классификатора для предсказания направления движения цены акций Apple. Сначала разберем основные принципы работы наивного байесовского классификатора, затем создадим простой пример использования дня недели для предсказания направления цены закрытия — выше или ниже текущей, а в окончании построим более сложную модель, включающую технические индикаторы.

Что представляет собой наивный байесовский классификатор (НБК)?

НБК старается найти вероятность события А при условии, что событие В уже произошло, обзначаемую как Р(А|B) (вероятность А при условии В).

В нашем случае, мы должны спросить: какова вероятность того, что  цена возрастет, при условии, что сегодня — среда? НБК берет во внимание обе вероятности — общую вероятность роста цены, то есть число дней, когда цена закрытия была выше цены открытия относительно всех рассматриваемых дней, и вероятность роста цены при условии, что сегодня среда, то есть сколько прошедших сред имело цену закрытия выше цены открытия?

( Читать дальше )

В последнее время приобретают все большую популярность алгоритмы машинного обучения. Они применяются для решения задачи классификации входных данных, или, проще говоря, выявления паттернов в структуре этих данных. Небольшой цикл статей про машинное обучение опубликован на сайте inovancetech.com, здесь я представляю их перевод.

В этой серии статей мы рассмотрим построение и тестирование простой стратегии машинного обучения. В первой части отметим основные принципы машинного обучения и их применение к финансовым рынкам.

Машинное обучение становится одной из самых многообещающих областей в алгоритмической торговле за последние два года, но имеет репутацию слишком сложного математического подхода. В действительности это не столь трудно в практическом применении.

Цель машинного обучения (МО) в том, чтобы правильно смоделировать исторические данные, и затем использовать эту модель в предсказании будущего. В алгоритмической торговле применяется два типа МО:

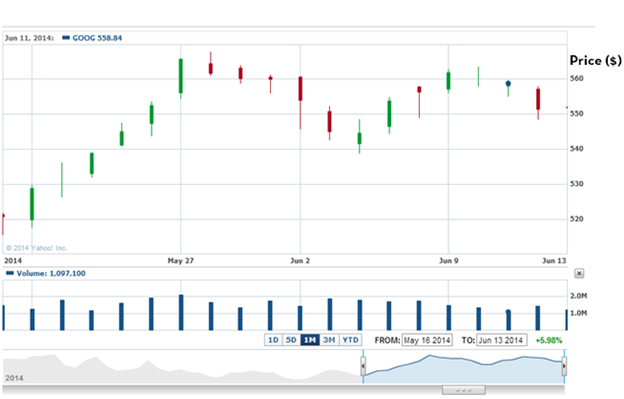
• Регрессия: используется для предсказания направления и амплитуды исследуемой величины. Например, цена акций Гугл возрастет на 7 долларов на следующий день.
• Классификация: используется для предсказания категории, например, направления движения цены акций Гугл на следующий день.

( Читать дальше )

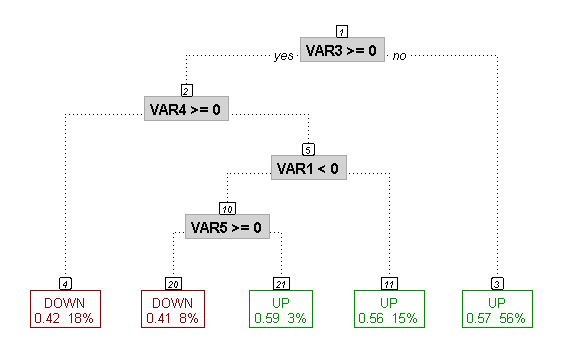
Интересный подход к предсказанию направления  рынка рассмотрен в статье "Using CART for Stock Market Forecasting". Для того, чтобы предугадать движение цены на недельном отрезке используется техника под названием CART (Classification And Regression Trees) — построение классификационного графа (дерева) с целью предсказать значение  целевой характеристики (цены) на основании набора объясняющих переменных. CART находит применение во многих областях науки и техники, но применим и в торговле, так как обладает набором свойств, хорошо подходящими для этой цели:

• может применяться при любом типе статистического распределения
• может применяться как для линейных, так и нелинейных зависимостей
• устойчив к событиям, выходящим за рамки статистических распределений

Для построения дерева автор использует библиотеку языка R, вычисляющую рекурсивное разделение (Recursive Partitioning) rpart.

( Читать дальше )

Продолжаю пополнять квантопедию смартлаба.
ЛЕКЦИЯ 1 «ПОСТАНОВКА ЗАДАЧИ. ВИДЫ ОБУЧЕНИЯ. “ДЕДУКТИВНЫЕ” И “ИНДУКТИВНЫЕ” МЕТОДЫ ОБУЧЕНИЯ»



Курс «Машинное обучение» 

16.02.2012, 18:30
Актовый зал, ФМЛ 239 (корпус 2)

Преподаватель

• Куралёнок Игорь Евгеньевич

На втором часу лекции лектор объясняет про нейронные сети. Помню была группа спорщиков которые пытались мне доказать что нейронные сети это не оптимизация в чистом виде. Вот как раз вам мнение авторитетного человека, о том что это все так и есть. Нейронная сеть = подгонка под кривую.

Доказав себе однажды, что ни один из индикаторов по отдельности или в совокупности с другими работают неудовлетворительно (по тестам от 3-х лет и более) я пришел к простейшим методам Data Mining, которые показали очень хорошие результаты. Пришла пора капнуть глубже, тут как раз и аккуратненькая подборочка, для поверхностного ознакомления, нашлась. 

А вы используете в своей торговле подобные штуки?

Метод опорных векторов
 



Метод опорных векторов был разработан Владимиром Вапником в 1995 году [86] и впервые применен к задаче классификации текстов Йоахимсом (Joachims) в 1998 году в работе. В своем первоначальном виде алгоритм решал задачу различения объектов двух классов. Метод приобрел огромную популярность благодаря своей высокой эффективности. Многие исследователи использовали его в своих работах, посвященных классификации текстов. Подход, предложенный Вапником для определения того, к какому из двух заранее определенных классов должен принадлежать анализируемый образец, основан на принципе структурной минимизации риска. Вероятность ошибки при классификации оценивается, как непрерывная убывающая функция, от расстояния между вектором и разделяющей плоскостью. Она равна 0,5 в нуле и стремится к 0 на бесконечности.




( Читать дальше )