алгоритм
Корреляция и структура корреляции
- 08 сентября 2015, 09:03
- |
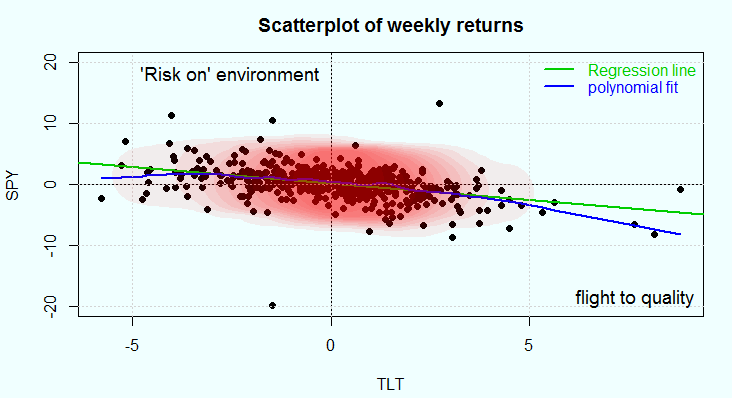
Интересные соображения по поводу вычисления правильной корреляции изложил в своем блоге Eran Raviv. По моему мнению данный подход можно попробовать использовать в статистическом арбитраже и парном трейдинге. Ниже даю полный перевод статьи с кодом на языке R.
В случае постоянной скорости, время и расстояние полностью коррелированы. Дайте мне одну переменную, я дам вам другую. Когда две переменные не имеют ничего общего между собой, мы говорим, что они не коррелированы.
Вы думаете, что это все, что можно сказать, но это не так. Как правило, ситуация более сложная. В большинстве обычных применений используется корреляция Пирсона. Коэффициент корреляции Пирсона отражает линейную зависимость. Поэтому мы говорим, что это параметрический показатель. На самом деле он может возвращать ноль даже если две переменные полностью зависимы ( наглядно показано здесь).
( Читать дальше )
- комментировать
- ★11
- Комментарии ( 2 )
Использование стоплоссов-3
- 25 августа 2015, 08:59
- |
В прошлой части мы проводили симуляцию для одного определенного процесса — геометрического броуновского движения с положительным дрифтом. Можно сделать подобный же анализ для более сложных и более реалистичных наборов данных. Мы можем добавить толстые хвосты распределения, ассиметричность и т.п. Также можно сделать результат одной сделки зависимым от предыдущих. Во всех этих случаях результат будет одним и тем же — стоплоссы снижают средний доход и меняют его распределение на что-то подобное бимодальному. Но что произойдет на реальном рынке, где процесс приращения цен неизвестен и точно не соответствует нормальному? Давайте перенесем теорию в реальную торговлю.
Очевидно, многие инвесторы используют стопы. Некоторые настаивают, что стоплосс абсолютно естественнен и его правильное использование приводит, в общем, к долгосрочной успешной торговле. Не будем принимать это утверждение на веру просто из-за его распространенности и проверим, так это или нет. Учитывая, что большинство тестов показывают — стопы стоят денег, что по этому поводу думают трейдеры?
( Читать дальше )
Использование стоплоссов-2
- 20 августа 2015, 08:51
- |
В прошлой части мы сделали теоретические предположения насчет влияния стоплоссов на общий результат торговой системы. В данной статье проверим эти утверждения на симуляции.
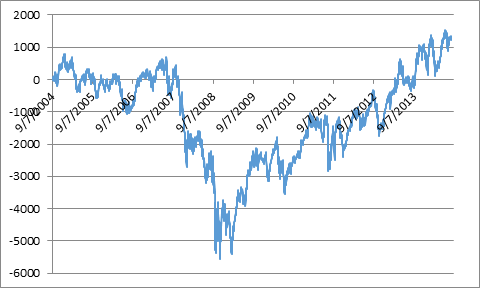
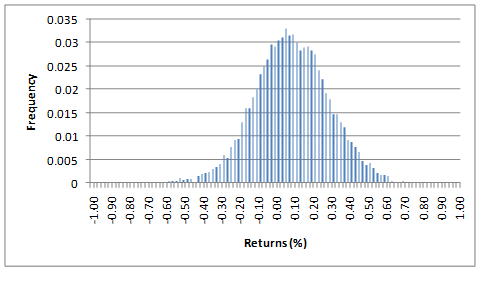
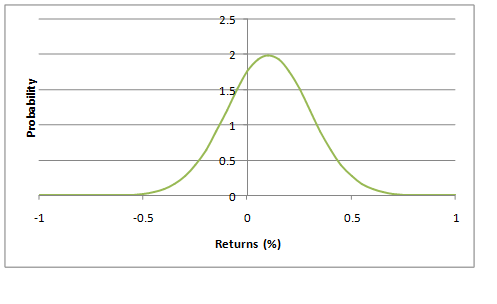
Симулируем десять тысяч сделок. Перед применением стопов мы получили распределение со средним значением 10% и стандартным отклонением 20%. Это похоже на производительность S&P500, начиная с 1950 года, этот контракт показал годовую доходность 7,4% и стандартное отклонение 15,4%. Результаты симуляции показаны на графике в заглавии.
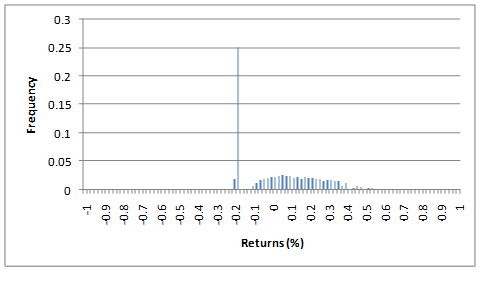
Теперь разместим стоп на уровне 15% ниже нашего начального вхождения. И получим распределение, показанное на рисунке ниже.
( Читать дальше )
Использование стоплоссов-1
- 18 августа 2015, 08:56
- |
Много дискуссий возникает на тему вреда или пользы применения стопов в трейдинге. Ответ на этот вопрос попытался дать автор блога blog.factorwave.com.
Вам не нужно читать много книг или статей по трейдингу, чтобы понять важность стоп-ордеров — определенных точек выхода для прекращения убытков и закрытия позиции. Обычно утверждается, что использование стопов естественно. Идея ограничения убытков больше определенного значения выглядит привлекательной. Что может быть неправильным, если мы обрезаем убытки и позволяем прибыли «течь»?
Но если что-то часто говорится, это необязательно должно быть правдой, не зависимо от того, кто это утверждает. Так что же действительно происходит, когда мы пытаемся следовать таким, вроде бы безобидным, высказываниям, в нашей торговле? Возможно, здесь есть преимущества, но во сколько они обходятся?
( Читать дальше )
Пример использования VPIN и модели Маркова в торговле
- 14 августа 2015, 08:56
- |
Насколько успешным может быть применение индикатора токсичности потока ордеров VPIN в трейдинге? А если попробовать соединить его с моделью скрытых состояний Маркова? Пример такой стратегии приводит Dr Jonathan Kinlay в своем блоге. Напоминаю, что всю теорию по расчету VPIN вы сможете найти на моем сайте здесь, а по модели Маркова — здесь.
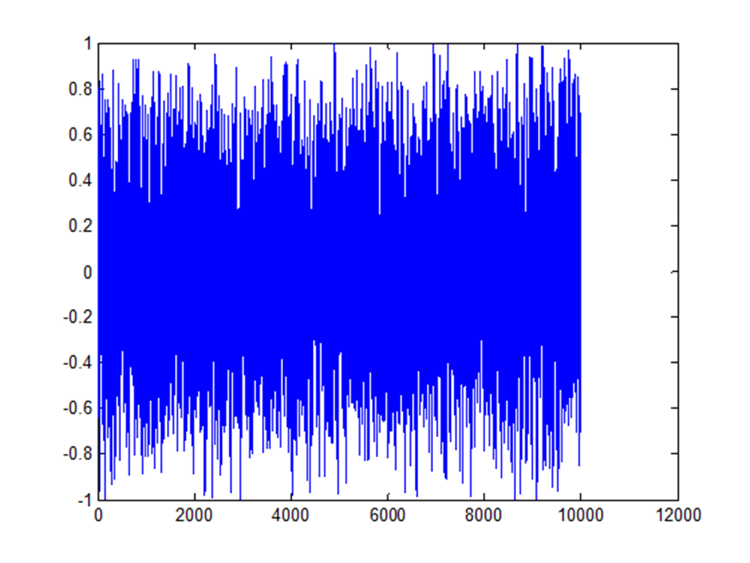
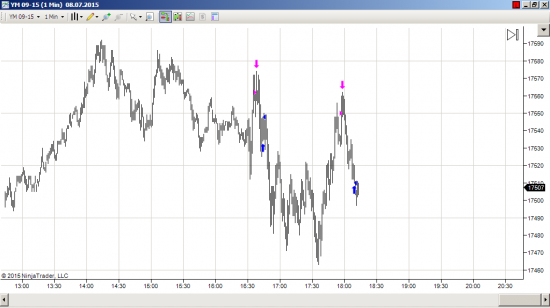
Для наших целей интерес представляет однопериодный знаковый VPIN. Он принимает значения от -1 до 1, в зависимости от пропорции между покупками и продажами за один период t — см. график в заглавии статьи.
Мы предполагаем, что приращение цены актива имеет сильную зависимость от значения VPIN. Например, в тестах фьючерса ES, мы увидели, что изменение средней цены от одного объемного пакета ( см. теорию VPIN) до следующего высококоррелировано со значением VPIN в предыдущем пакете с коэффициентом 0,5. Другими словами, участники рынка, предоставляющие ликвидность, будут обновлять свои ордера в направлении, которое прямо связано с направлением и интенсивностью потока токсичности.
( Читать дальше )
Корреляционный сигнал
- 31 июля 2015, 09:01
- |
Использование корелляции широко распространено в финансовой теории и практике, от создания портфелей до стратегий статистического арбитража.
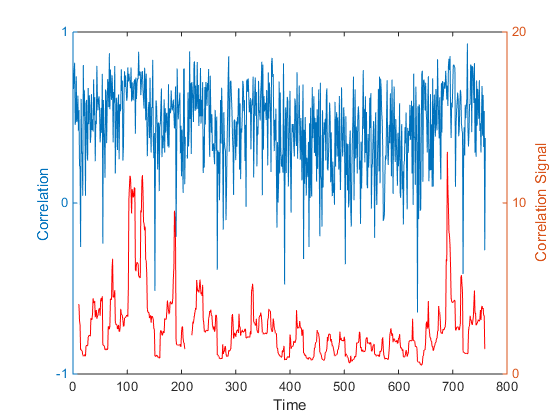
Основная сложность в применении корелляции это ее изменчивость: активы, которые в один момент времени кажутся практически некоррелироваными для целей хеджирования, могут стать высококореллироваными в другие моменты времени, например, при высокой активности рынка. Напротив, акции, кажущиеся подходящими для парной торговли, в связи с высокой корелляцией их приращений цены, могут позднее показать разнонаправленную динамику, приводящую к значительным потерям.
Нестабильность уровня еще усугубляется эмпирическими выводами о том, что волатильность корреляции сама по себе зависит от времени: в одно время корреляция между активами может плавно меняться в узком диапазоне, в другое время мы можем наблюдать изменения знака коэффициента корелляции в течении нескольких дней.
( Читать дальше )
Волатильность как актив-2
- 29 июля 2015, 09:08
- |
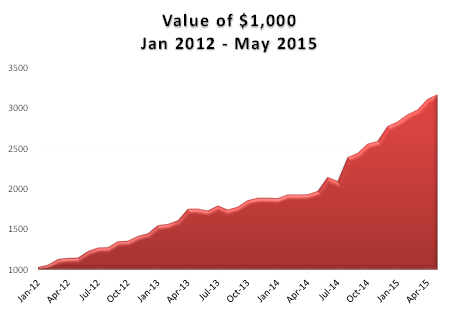
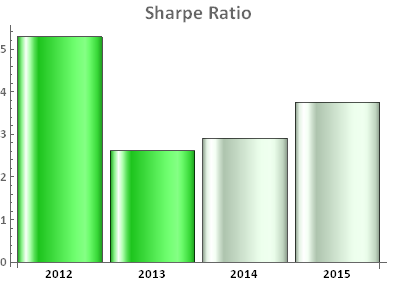
Вывод, который мы можем сделать из первой части данной статьи такой: почти все стратегии, которые мы знаем, имеют эквивалент в пространстве волатильности, будь это покупка/продажа волатильности, статистический арбитраж или следование за трендом. Более того, из-за особых характеристик волатильности, все эти стратегии имеют тенденцию к большей производительности, чем их традиционные аналоги. В пример автор приводит показатели собственной стратегии на волатильности биржевых фондов ETF, которая имеет устойчивый годовой доход между 30% и 40%, с коэффициентом Шарпа более 3, начиная с 2012 года (см. графики в заглавии и ниже).
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал