алготрейдинг
алготрейдинг - подход к биржевой торговле, основанный на автоматизации торгового процесса при помощи программных алгоритмов и различных аппаратных решений.
Ниже приведены все записи на нашем сайте по теме алготрейдинга.
#SensorLive - Day393-395
- 01 ноября 2016, 09:55
- |
Прямая трансляция торговли на сегодня: 01.11.2016
Начало проекта тут.
( Читать дальше )
- комментировать
- Комментарии ( 2 )
Алготрейдинг
- 31 октября 2016, 01:09
- |
Индикатор для QUIK
- 30 октября 2016, 22:40
- |
Вот пример на нефти, ТФ 2 часа:
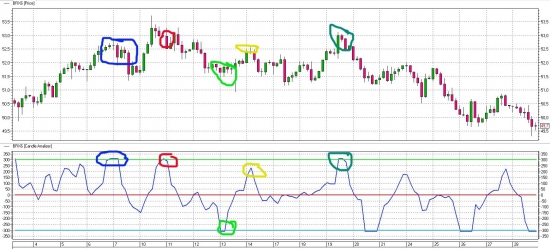
Когда пересекается верхняя линия — можно задуматься о продажах, соответственно, нижняя — о покупках.
P.S.Просьба не рассматривать как «грааль» — при принятии решения о сделке нужно подтверждение дополнительными сигналами.
Скачать: yadi.sk/d/WAJuUeDkxqyMU
Опросник для тестирования квалифицированных инвесторов ?
- 30 октября 2016, 15:43
- |
Друзья, давайте поможем создать опросник для автоматического тестирования трейдеров и присвоение им квалификации. Нужны контрольные вопросы и варианты ответов. Как в ЕГЭ. Я начну, а вы продолжите.
1 Набтулина это кто?
А Банкирша
Б Стриптизерша
В Ведущая телешоу
2 Герчик это кто?
А Брокер
Б Трейдер
В Ни кто
3 ОФЗ как расшифровывается
А Объеденный федеральный заказ
Б Облигации федерального займа
В Ответ фашистам на закон.
4 Forex это:
А Кухня
Б Ресторан
В Менялка валют
5 Лось это:
А Лось
Б Удачно поставленный ордер лимитный
В Не удачно поставленный ордер по рынку
6 Если у вас 399 000 рублей вы можете купить:
А ОФЗ
Б ЗВР
В ВВП
И Т.Д.
Хотелось бы услышать мнение профессионалов какие еще вопросы необходимы, что бы определить профпригодность трейдеров и инвесторов. Вопросы давайте в комментарии. Ответы тоже. Проверим ваши знания.
#SensorLive - Day389-392
- 27 октября 2016, 09:57
- |
Прямая трансляция торговли на сегодня: 27.10.2016
Начало проекта тут.
( Читать дальше )
Раз пошла такая пьянка
- 26 октября 2016, 20:53
- |
В текущем ЛЧИ робота Секрета нету и уже не будет.
Секрет не участвует в ЛЧИ. Официальное подтверждение будет после ЛЧИ.
Косвенные факты: Ни один из заявленных роботов не отвечает характеристиками набора доходности в стиле Секрета.
По этому текущий ЛЧИ будет вялым, тухлым и без драйва. Люди все уже в курсе, но что то никто не посмел открыто об этом заявить.
Торговля роботом, внутри трендового канала
- 25 октября 2016, 19:26
- |
Всех приветствую.
Сегодня без видео! хотел записать в белой теме, но возникли сложности, и без мата не получалось записать.
В целом ничего сложного, на примере обычного хай лоу робота, я реализовал стандартную трейдерскую фантазию, «А что если нарисовать вручную некий канал, в котором робот торгует по заданной логике?!»
Сказанно — сделанно!
сам скрипт выложен на форуме TSLab http://forum.tslab.ru/ubb/ubbthreads.php?ubb=showflat&Number=79922 (скопируйте ссылку в браузер, такая странная особенность)
В скрипте помимо стандартного хайлоу, добавленны только интерактивные линии, это непосредственно те самые линии которые можно вручную нарисовать на графике и добавить в логику агента.
в итоге получилась такая картина
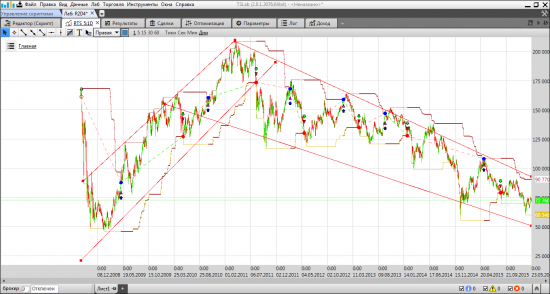
Данных много (8лет ртс) потому на дневном графике рисовал каналы, а на минутке уже основная статистика.
Картинка эквити (40п на круг) при торговле если растущий канал то только лонг если падающий то только шорт
( Читать дальше )
Тейк-профит VS Стоп-лосс. Что выбрать 1:1, 1:3, 3:1?
- 25 октября 2016, 16:01
- |
Материал предназначен для начинающих трейдеров.
Как прибыльнее торговать, с коротким стопом и большим тейк-профитом или наоборот? И насколько один должен превышать другого? А может быть они должны быть одинаковыми?
Интересно? Проверим на исторических данных?
Поехали!
Рассмотрим классическую стратегию пересечения двух скользящих средних. Будем использовать индикатор МА (Moving Average). Если быстрая скользящая средняя пересекает медленную скользящую среднюю снизу вверх, то открываем Лонг. Пересечение является сигналом на вход в позицию. Если пересечение в обратную сторону, то открываем Шорт. Выставляем заявки стоп-лосс и тейк-профит. Ждем какая из них отработает.
Получилась вот такая логическая схема робота:

( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал