аудит
Сверхприбыльная алготорговля на FOREX - всегда развод? Тимофей Мартынов не даст соврать.
- 11 января 2021, 14:44
- |
Однако, в мониторингах полно сверх-прибыльных FOREX-счетов. 99% из них — результат торговли на них роботов.
Это всегда развод? Или все же в этом мраке есть реальные алмазы: спрехприбыльная торговля была выгодна и алготрейдеру и брокеру, неоднократные выводы прибыли, во много превышающие начальный депозит. Неужели такое может быть на этом FOREX?

Я нашел людей, утверждающих, что могут доказать, что такое бывает. При этом готовы заплатить крупную сумму в том случае, если им не удастся доказать это. Мы то все знаем, что где-то подвох и такого быть не может. Они готовы отвечать за свои слова крупными деньгами, да еще вот так открыто переть против мнения массы фондовиков на биржевом ресурсе. Так что возможность уникальная раз и навсегда поставить жирную точку по этой теме.
( Читать дальше )
- комментировать
- ★2
- Комментарии ( 132 )
Криптовалюты & Юриспруденция (правовые аспекты, юридический опыт в делах связанных с криптовалютами)
- 21 мая 2019, 13:06
- |
Как оказалось, ввиду отсутствия надлежащего правового регулирования в сфере блокчейна и криптовалют, и отсутствия соответствующей практики, возникающие проблемы накладывались одна на другую. В поисках решения, мне посоветовали Smart-Lab.
Теперь к сути-возникла необходимость в проведении аудита аккаунта криптовалютной биржи с последующем предоставлением экспертного заключения имеющим юридическую силу(следствие, суд). В заключении эксперту необходимо ответить на ряд вопросов таких как: сколько средств заходило, сколько уходило, суммы убыточных сделок и тд за определенный период.
Если есть кто сталкивался с подобным, прошу поделиться опытом и контактами, куда можно обратиться для получения вышеуказанного заключения?
заранее спасибо за отзывы.Было мнение что для дачи заключения, достаточно квалификации специалиста, который ведет деятельность официальную и у него открыты оквэд на биржевой вид деятельности, где поискать такого?
Подавляющее большинство зарегистрированных доходов компаний – без аудита!
- 08 февраля 2019, 15:59
- |

Данные, предоставленные Audit Analytics, показывают, что только шесть из 174 компаний, которые сообщили о прибыли в январе, сделали это с полным аудитом.
Подавляющее большинство компаний, которые сообщили о своих доходах за четвертый квартал в период с 1 января по 1 февраля, сделали это без завершения аудита, что, по мнению экспертов, может иметь неприятные последствия.
Данные, предоставленные исследовательской фирмой Audit Analytics, показывают, что из 174 компаний с рыночной капитализацией не менее 10 миллиардов долларов, которые сообщили о прибыли за этот период, только шесть подали свои 10-K, и аудиторы отчитываются перед Комиссией по ценным бумагам и биржам в тот же день или ранее.
Это означает, что оставшиеся 168 опубликовали неаудированные цифры за весь год или только частично проверенные цифры с объявлением о доходах. Недавнее исследование показало, что аудиторы в этой ситуации могут чувствовать давление, чтобы придерживаться уже опубликованных цифр и не хотят предлагать исправления или корректировки.
( Читать дальше )
Юмор с ZeroHedge — Йеллен на слушаниях в Конгрессе
- 12 июля 2017, 22:49
- |
Твое лицо, когда тебе предлагают провести аудит твоего Центрального Банка:
На фотографии, «Новости в студию (Breaking News): Йеллен: Я категорически против аудита ФРС (I’m strongly opposed to audit the FED)».
____
мой блог
( Читать дальше )
Фундаментальные основы аудита.
- 14 декабря 2016, 00:37
- |
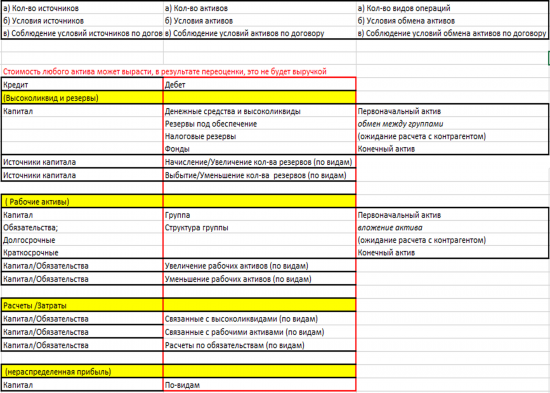
( Читать дальше )
ЦБ будет публиковать результаты фин. аудита некредитных организаций и эмитентов
- 06 июля 2016, 11:52
- |
Новшества коснутся страховых компаний, УК, НПФ, клиринговых организаций и эмитентах, ценные бумаги которых включены в котировальный список.
(Пресс-релиз)
Демократы "зарезали" Закон об аудите ФРС в Сенате
- 13 января 2016, 07:10
- |
Закону не хватило 7 голосов — республиканцы голосовали почти единогласно «за». Рон Пол не унывает и говорит, что «еще один крупный экономический коллапс может изменить умы».
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал

