случайное блуждание

М-да...

И все ж таки — какой же на рынке процесс? Случайный али нет? Есть ли хотя бы надежда припасть к Граалю и напиться из него Счастия?

Собственно говоря, неважно — какое именно уравнение описывает динамику рынка:

марковское


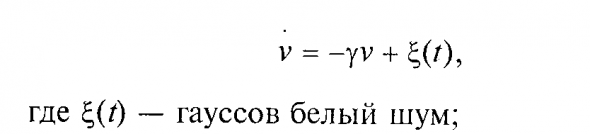
или немарковское:


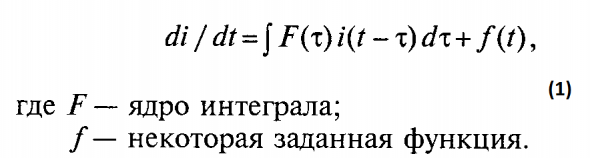
( Читать дальше )

Привет, господа трейдеры!

Пока идут испытания моей ТС, мне в ЛС поступают вопросы от страждущих. На один из них хотелось бы ответить публично, т.к. на распространение этой информации получено разрешение от ее владельца.

Вопрос: кто такой Колдун и почему так часто я упоминаю Его в своих постах?

Хе-хе...
Колдун…
Личность легендарная и загадочная. Не часто он выходит на связь и отличается особыми приемами подачи информации. По Его словам — обладает Граалем, не нуждается в помощниках, учениках, друзьях и т.п. Очень хорошо разбирается в нейросетях, насколько я понимаю лично знаком с д.ф.-м.н. Воронцовым К.В. (подозреваю, что это Он и есть либо кто-то из его учеников). По его комментариям к опытам и исследованиям страдальцев можно судить о глубоком понимании обсуждаемых проблем. Все свои комментарии, подсказки, графики, формулы и т.п. через некоторое время удаляет — так что можно их и не искать, а общаться с ним On-line если повезет встретить.

Я с ним пересекался при обсуждении возможности использования стратегии заработка на случайном блуждании (см. 

( Читать дальше )

Не найдя теоретического ответа, выполнил-таки численное моделирование винеровского процесса (случайного блуждания). А именно — OHLC-баров, сформированных суммированием шагов (приращений), имеющих гауссово распределение N(0, 1) (см. «преобразование Бокса — Мюллера»).

Если взять O (Open бара) за ноль и  привести бар к нормировке StDev( С)=1, то получились следующие статистики:

Avg(Abs( С)), Avg((H-L)/2),Avg(H), Avg(-L) — между 0.788 и 0.79

— причем Avg(Abs( С)) находится в этом диапазоне практически уже при малом количестве шагов (на бар), а вот остальные три величины приходят туда только после 5000 шагов на бар. Видимо, это связано с тем, что "... the algorithm will not produce random variables more than 6.660 standard deviations from the mean" (это про преобразование Бокса — Мюллера в https://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform )

Статистика Avg(Abs( С)/(H-L)) начинается выше 0.5, но к 10000 шагов на бар опускается до 0.46 (объяснение, видимо, то же самое).

Может кто-нибудь сформулировать критическую позицию относительно этих результатов? 

Известен методологический принцип, согласно которому никакая торговля случайного блуждания не может быть систематически доходна.

Однако, внимание, магия!

Пусть мы торгуем произвольнуый ряд значений цены фишки Ф (в том числе, например, и случайное блуждание) при помощи Trailing Stop величиной 10 пипсов и такого вот забавного способа входа: если у нас нет Ф, то мы сразу же её покупаем. А купив — трейлим, как я уже сказал. И без комиссии.

Однако сначала поторгуем «виртуальный Trailing Stop», то есть не будем ставить его «в ордер», но будем держать в голове, и когда он будет «срабатывать», то мы будем закрывать позицию (продавать) по «рыночной цене».

Итак, сработал «виртуальный Trailing Stop», мы закрылись по следующей цене Р… Но раз мы закрылись, значит у нас нет фишки, значит мы должны сразу купить по цене… Р (по которой мы закрылись). То есть такая торговля с виртуальный Trailing Stop эквивалентна тому, что у нас постоянно на руках фишка Ф. А значит, у нас нет ни прибыли, ни убытка.

( Читать дальше )

Есть гауссово случайное блуждание:

P(i) = P(i-1) + N(0, 1)

Оно разбивается на последовательные отрезки по ̲1̲0̲0̲0̲0̲ ̲ш̲а̲г̲о̲в̲, которые преобразуются в OHLC бары B(k) слегка специфического вида — а именно в качестве Open бара B(k+1) проставляется Close бара B(k).

Нативные обозначения: O(k), H(k), L(k) и C(k) — значения открытия, хая (максимума), лоу (минимума) и закрытия бара B(k).

Если рассмотреть отдельно ряд C(k), то он соответствует «описательной» формуле:

С(k) = C(k-1) + N(0, 100)

(если вы не понимаете, почему это так, то вам лучше дальше не читать).
_______________________________

Введём в рассмотрение случайные величины:

OC = O(k) — C(k)
HС = H(k) — C(k)
CL = C(k) — L(k)

Тогда «статистика» ( = статистический закон распределения) величины OC — это есть N(0, 100).



( Читать дальше )

Что такое случайное блуждание цены


( Читать дальше )

Господа!

В связи с тем, что ТС, основанная на немарковской модели рынка, дает весьма обнадеживающие результаты:


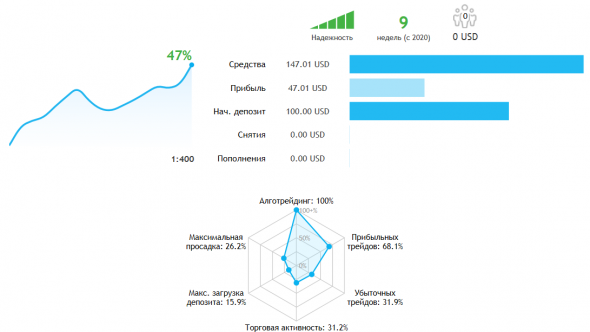
цикл статей, посвященный метОдам заработка на случайном блуждании:
https://smart-lab.ru/blog/636953.php
https://smart-lab.ru/blog/616897.php
https://smart-lab.ru/blog/613005.php
https://smart-lab.ru/blog/609057.php
https://smart-lab.ru/blog/608175.php
https://smart-lab.ru/blog/582407.php
https://smart-lab.ru/blog/580961.php
https://smart-lab.ru/blog/579572.php
аннулируется.

Прошу модераторов СмартЛаба удалить эти посты, дабы страждущие, узрев их, не пошли по дороге в Бездну.

На рынке нетути случайного блуждания.
Toddler.

У последователей случайного блуждания есть такая забава: имитируется случайный процесс с вероятностью выпадения -1 или +1 равной 50%. Раньше это делали подбрасыванием монетки (см. например книгу «Случайное блуждание по Уолл-Стрит»), сейчас – на компьютере. Когда для генерации случайного числа использовали монетку, то обычно ограничивались несколькими сотнями реализаций. Но компьютер позволяет легко сделать сколько угодно реализаций и это меняет восприятие.

По идее график должен колебаться около нуля, но порой получаемые картины эквити поражают воображение (см. ниже диаграмму, число реализаций 10000). Как тут не поверить, что за этими диаграммами стоит нечто «реальное», толкающее графики вверх или вниз. Глядя на эти графики, одна часть мозга говорит, что это абсолютно случайный процесс, а другая часть мозга «видит» совершенно осмысленное движение, на котором можно заработать (это я уже о рынке).

( Читать дальше )

Эх, чувствую, зреет срач (в хорошем смысле слова) между тех.аналитиками (в т.ч. волновиками) и любителями мат.статистики. Поскольку главный волновик, т.е. командовать парадом, буду я, позволю себе набросить каку небольшую мысль на вентилятор для обсуждения.

Участники рынка действуют, глядя на рыночную ситуацию, принимая решения исходя из неё. Рыночная ситуация меняется вследствие их действий. Это можно считать случайным блужданием?

    Обо что ломаются копья в спорах о случайном ценообразовании на рынках? Кто спорщики? Есть ли однозначный ответ или в рынке все условно?

    Спорщики, как обычно, это «физики и лирики». В нашем случае – математики и нормальные люди))). Я себя отношу и к тем и другим, как в анекдоте: умные налево, красивые направо, а мне что, разорваться?)))

    Квантовая физика, лежащая в основе моей первой специальности (физика твердого тела), и являющаяся идеалом случайных процессов, должна бы, по идее, поместить меня в лагерь сторонников случайных блужданий, если брать их строгое математическое определение: Если невозможно предсказать точно знак следующего приращения цены, значит этот процесс случайный, а сумма случайных приращений есть, разумеется, величина случайная, а значит и весь процесс ценообразования можно определить как случайное блуждание. Вроде, все логично и спорить тут не с чем… Но «что-то меня терзают смутные сомнения» © )))

( Читать дальше )