случайный процесс
Модель рынка как немарковского процесса. Часть 3. Тестовый Грааль
- 02 июня 2020, 13:08
- |
А чего это мы все тут делаем? Ах, да! Грааль ищем.
Так вот, рассмотрим еще раз интегро-дифференциальное уравнение для немарковских процессов

Функция f(t) характеризует поведение системы без учета памяти и, применительно к рынку, имеет смысл гауссовского «белого шума».
Проинтегрировав уравнение (1) получим, что цена i(t) описывается:
а) скользящей средней:
( Читать дальше )
- комментировать
- ★10
- Комментарии ( 28 )
Как заработать на случайном блуждании. Часть 6.
- 25 апреля 2020, 20:44
- |
В продолжение темы https://smart-lab.ru/blog/612608.php, хотелось бы добавить небольшое исследование.
Итак, мы остановились на том, что приращения рыночных котировок представляют собой расстояния, которое проходит броуновская частица за экспоненциальное время.
Еще раз смотрим на интегрированный процесс по таким приращениям:
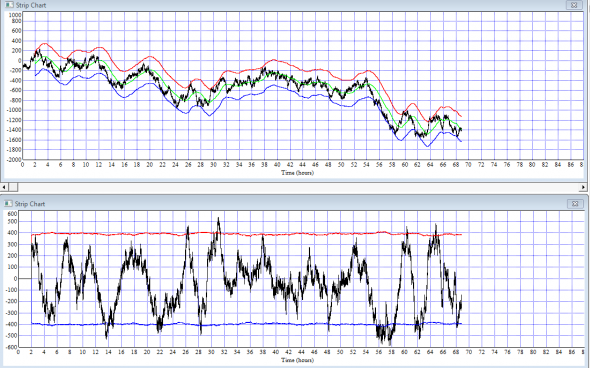
Хорошая модель, но… Не хватает главного — ответа на вопрос: а откуда берется нестационарность дисперсии реального рыночного процесса?
Ведь дисперсионный канал ±(sqrt(2*D*t)) на нижнем графике суммы приращений в скользящем временном окне практически =const, а на деле:
( Читать дальше )
Как заработать на случайном блуждании. Часть 5
- 12 апреля 2020, 14:42
- |
Иногда мне кажется, что Он рядом, только руку протяни, ан — нет, не все так просто. Но, жажда напиться из Него — безмерна. Продолжим наш путь.

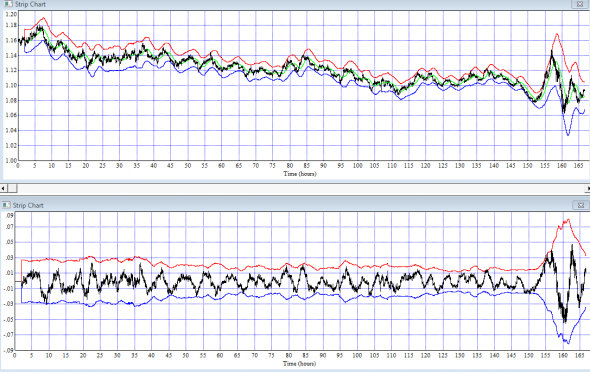
Сегодня постараемся смоделировать распределение приращений цены. Ведь мы же помним, что оно выглядит вот так:
( Читать дальше )
Модель рынка как немарковского процесса. Часть 2.
- 08 апреля 2020, 21:09
- |
Се ля ви… Нам надо, во что бы то ни стало, найти Грааль. Мы верим, что на рынке немарковский процесс, процесс с памятью, когда цена зависит от всех предыдущих своих значений или, по меньшей мере, от значений внутри временных циклов рынка.
А как же марковская модель? Применима ли она к рынку? Не в том ли проблема, что мы уверены, что будущие значения цены зависят только от текущего значения цены и ее скорости, а все предыдущие значения отказываемся принимать в расчет — ведь в этом смысл модели Маркова, не так ли?
Для ответа на этот вопрос, нам потребуется рассмотрение уравнение Фоккера-Планка (или прямого уравнения Колмогорова). Оно выводится для системы хаотически движущихся (броуновских) частиц, т.е. диффузионного облака молекул.
В общем случае, оно выглядит так:

( Читать дальше )
Как заработать на случайном блуждании. Часть 4
- 29 марта 2020, 12:08
- |
Доброго времени суток, господа!
М-да… Вся лента забита новостями: коронавирус, нефть-матушка, кризис...
А где же будоражащие душу исследования, напрямую ведущие к Граалю? Нетути… Нетути Грааля аль, все ж таки, есть?
Продолжим путешествие в мир случайности/закономерности рыночных временных рядов с целью узреть Свет и Счастие для всех страждущих.
В предыдущих частях проекта:
https://smart-lab.ru/blog/579572.php
https://smart-lab.ru/blog/580961.php
https://smart-lab.ru/blog/582407.php
мы убедились, что заработать на теоретических случайных процессах («монетка», Laplace motion, ...) довольно просто. Пользуемся тем фактом, что сумма независимых или слабозависимых случайных величин (приращений) дает число, принадлежащее нормальному распределению Гаусса и при выходе текущей кумулятивной суммы за пределы диапазона +-Delta*1.96, где Delta = sqrt(2*(b^2)*t), заключаем сделки, а при возврате в 0 — закрываем их. Дело сделано...
( Читать дальше )
Как заработать на случайном блуждании. Часть 3
- 21 декабря 2019, 00:11
- |
Почему он гораздо сложнее пресловутой «монетки»? Как вообще такое может быть, что на обычном случайном блуждании мы спокойно зарабатываем, а на рынке ничего не получается? Откуда берутся гигантские импульсные движения цены?
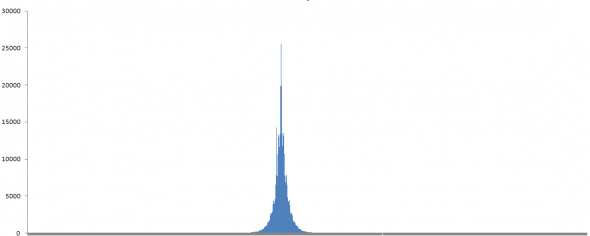
Для попытки ответа на эти вопросы, в первую очередь мы рассмотрим распределение вероятностей приращений (первых разностей цены) CLOSE M1 для пары EURUSD за 2018 г.
Оно всем известно и загадочно. Выглядит оно вот так:
Еще никому не удалось понять — почему оно такое, островершинное и тяжелохвостое. Откуда оно взялось и как его смоделировать?
Постараемся ответить на эти вопросы. Не сейчас, не быстро, но, думаю у нас это получится.
В первую очередь попробуем аппроксимировать его обычным (обычным ли?) треугольным распределением.
Совсем простым — как сумму двух равномерно распределенных величин. Как будто бросаем 2 монетки (ведь мы же помним, что Волшебник говорил, что на рынке мы видим суперпозицию именно двух процессов, не так ли?) и два полученных результата просто суммируем.
( Читать дальше )
Как заработать на случайном блуждании. Часть 2
- 14 декабря 2019, 13:14
- |
Начало здесь - https://smart-lab.ru/blog/579572.php
В прошлый раз мы рассмотрели метод, дарованный свыше, применительно к случайному блужданию.
Уважаемые трейдеры моментально побежали применять его к рынку и… тут же выразили свое недовольство, что он не работает. :)))
«Сомнения рождают страх, страх рождает ненависть...» — так в народе говорят, что ли?
Я тоже сомневаюсь — честно говоря, никогда не пробовал ранее его в деле. Ну, давайте посмотрим.
Минуя исследования гауссовских и лапласовских случайных процессов, побегу-ка я, сломя голову, исследовать реальный рыночный ВР.
Рассмотрим пару EURUSD с 01.01.2019 по 08.12.2019 на ценах закрытия CLOSE M1
Выборка данных = 349716 значений, скользящее окно = 7200 (как и в эксперименте для «монетки»).
Конечно, рыночный ВР сложнее и говоря о применимости соотношения Sigma*sqrt(T) для вычисления стандартного отклонения процесса, прежде всего необходимо научиться правильно вычислять Sigma. Для «монетки» Sigma=1. А для рыночного ВР?
( Читать дальше )
Как заработать на случайном блуждании. Часть 1
- 08 декабря 2019, 16:05
- |
Начиная серию публикаций о способе заработка на случайных процессах и, в частности, на классическом случайном блуждании (т.н. «монетке»), я преследую одну цель — дать возможность трейдерам переосмыслить свои взгляды на рынок.
Поехали!
Итак, первым экспериментом будет «монетка». Да-да, обычный random walk — суммирование приращений +1 и -1, вероятность выпадения которых на каждом шаге итерации = 50/50.
Выборка данных = 349716 значений (сделано это для исследования работоспособности предлагаемого метода заработка на паре EURUSD с 01.01.2019 по 08.12.2019 на ценах закрытия CLOSE M1, которое будет произведено позднее).
Выглядит случайное блуждание так:
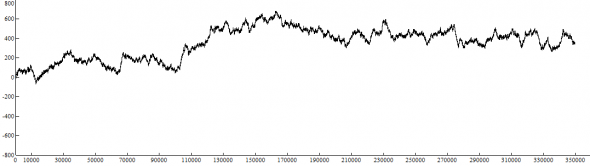
Считается, что на таком процессе невозможно заработать. Так ли это?
Воспользуемся методом скользящей кумулятивной суммы приращений.
Выберем скользящее окно данных = 7200 значений, что соответствует недельному скользящему окну по EURUSD на ценах закрытия CLOSE M1.
( Читать дальше )
Торгую случайный процесс. 314% прибыли в подтвержденной торговле за четыре месяца методом торговли случайного процесса.
- 03 апреля 2019, 14:34
- |
Главное: гораздо проще и легче выучить раздел Теории вероятностей и прибыльно торговать случайный процесс, чем бесконечно искать неизвестно что и неизвестно где в надежде найти «ВОЛШЕБНУЮ ЗАКОНОМЕРНОСТЬ РЫНКА и всегда зарабатывать».
------------------------------------------------
Вот отрывок из моей дискуссии с одним трейдером:
------------------------------------------------
Многие как бы трейдеры всё пытаются придумать какую-нибудь фишку или хитрую хитрость и обмануть-обыграть рынок и взять приз-бабки.
Ну уже понятно давно, что это не работает.
Оглянитесь вокруг себя — везде, вся техника и все вещи — всё создано и работает на научной основе. Почему то никто не будет строить самолет на основе своих догадок и придумок.
А вот как деньги заработать на бирже многие почему то уверены, что они, не имея научной подготовки и научных знаний, смогут придумать такую фишку, что легко будут стричь бабки на бирже.
Согласитесь, что это просто детская наивность.
Основные мысли —
1)сумма множества случайных величин (процессов) дает неслучайный, практически детерминированный, как бы предопределенный результат.
2) сумма множества случайных величин (процессов) имеет нормальное распределение, что на обычном языке означает «практически неслучайное поведение» случайной величины (процесса), что дает в результате нормальную работу «скользящих средних».
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал

