шарп

Тут после последнего топика народ почему-то решил, что я иксперд по трейдингу, и пишет всякое разное. Один из присланных вопросов звучал примерно так:

Я новичок, хочу уйти от дяди, помогите сделать рабочую ТС, для начала хватит Шарпа 1, доходности 15-20% годовых с просадкой не более 10%.

Я, признаться, растерялся, что ответить — для специалиста это звучит примерно так: научите, плиз, по-быстрому рисовать, для начала сойдет как Сальвадор Дали, а дальше я уж как-нибудь сам.

[Вру, на самом деле я не растерялся и ответил:

Если ретурн 15-20% и шарп 1, то и волатильность будет 15-20%. А с волатильностью 15-20% надо ожидать просадки 30-40%, а никак не 10%. То есть вы разберитесь, чего вы хотите. Если доходности 20% — готовьтесь к просадке 40% с шарпом-то 1. Если просадки 10% — значит, доходность ожидаемая должна быть 5%, ну пусть 10% от силы. А если вам и то и то — то шарпа надо с такими запросами в районе 3. А такой шарп есть только у ХФТ либо у пары-тройки больших хорошо диверсифицированных фондов (на всей планете).

]

( Читать дальше )

Прошу помощи от трейдерского комьюнити! 
Торгую фьючерсными на Мосбирже. Несколько стратегий, частые сделки, ввод-вывод средств. Задача посчитать доходность и риск по портфелю за всю историю и помесячно. Доходность в годовых, просадка, альфа, бетта, шарп и т.д. Как считаете? Может есть хороший ресурс где почитать/посмотреть/подглядеть. Теорию знаю, нужны практические советы, как из брокерского отчета данные перевести в статистику. Возможно кто-нибудь применяет Python для таких расчетов, за идею буду очень благодарен. Памагите, плиас)

По-моему все слышали про случаи ультимативной победы разных животных над паршивыми инвесторами. 

( Читать дальше )

Дополнение к серии «Портфельная оптимизация как бустинг на слабых моделях»

• Обобщённая проблема

Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.

Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:


 

где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.

( Читать дальше )

Устойчивые долгосрочные модели


В предыдущих частях (часть 1, часть 2) мы рассмотрели построение композитных систем оценок ценных бумаг, построенных при помощи распространённых средств машинного обучения (Bag/Boost методы). Однако, такой подход, несмотря на все свои преимущества (скорость, точность) имеет ряд больших недостатков – отсутствие универсальности моделей в результате проблем «переобучения»  (точной настройки на определённые типы рынков и временные интервалы) и сложность интерпретации полученных композиций.

В результате решения этих проблем мы разработали базовую модель на основе наших представлений о стохастических дифференциальных уравнениях с квантовыми скачками, образующих улыбку волатильности. Эта макромодель получила в наших исследованиях наиболее полную микроскопическую интерпретацию.

( Читать дальше )

Часть 2.

В прошлой части мы подбирали такую комбинацию статистических оценок динамики акций, которая давала нам возможность стабильно выбирать портфель акций лучше среднерыночного,  с показателем Шарпа на 26% выше индексного.

Мы также пробовали составлять портфель из портфелей и портфель на основе портфеля оценок, но в силу высокой линейной зависимости оценок и полученных на них портфелей друг от друга Bagging ожидаемо не дал никакого результата.

Тем не менее, этот важный этап подготовительных работ – построение портфеля (или композиции портфелей) на простых, статистических оценках дал нам некоторую отправную точку, относительно которой мы будем рассматривать эффективность всех наших последующих нововведений.

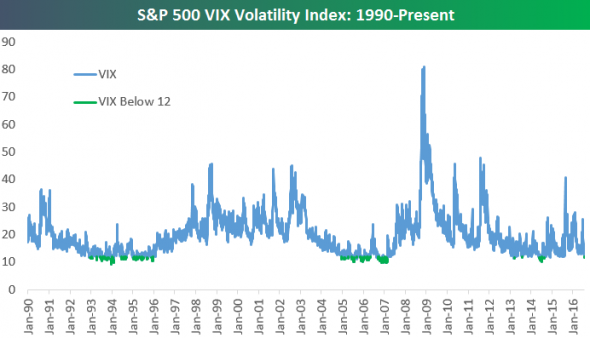
Рис. 6. Иллюстрация динамики волатильности акций США, входящих в состав индекса S&P 500.

 

Основную проблему стандартных методов мы видим в том, что они разработаны для стационарных стохастических процессов, в то время как любые финансовые (а зачастую природные, биологические и др.), временные ряды имеют нестационарную природу. Так, например, широко известно, что логарифмическое изменение стоимости акций является нестационарным процессом со склонностью к консолидации (кластеризации) волатильности.

( Читать дальше )

     В задачах оценки бизнес проектов, прогнозирования спроса, определения справедливой цены опциона или портфельного инвестирования, так или иначе, возникает проблема адекватной оценки рисков.  Обычно за риск принимается простое, выборочное среднеквадратичное отклонение, для которого хорошо разработан аппарат математической статистики, позволяющий прогнозировать критические показатели, например просадки,  и проводить стресс-тесты в предположении центральной предельной теоремы, то есть в предположении узкой стационарности  наблюдаемых процессов.

     Однако, мы зачастую имеем дело с абсолютно  другими, нестационарными процессами. Не стационарность процесса может быть вызвана  как нелинейным синергетическим эффектом  (реклама и «сарафанное радио»,  мода, политические выборы, революции и пр. самоорганизации),  как множественностью состояний системы (тренд/флэт), так и просто  некоторой инерцией системы, связанной, например, с задержкой принятия решений основными игроками.

( Читать дальше )

Часть 1.

Традиционно считается, что задача портфельной оптимизации, или задача Марковица, представляет собой некоторую самостоятельную задачу выбора такого портфеля активов, который обладал бы максимальной доходностью при минимальных рисках.

Прим. В качестве актива могут выступать ценные бумаги (акции), их производные (опционы)  или торговые системы.

 

Решение задачи состоит из двух этапов:

1. Прогноз доходности и ковариации активов в будущих периодах – то есть построение некоторого набора «слабых» прогностических моделей.
2. Составление оптимального портфеля в соответствии с некоторой целевой функцией, и ранее полученными оценками. То есть построение такой композиции «слабых» моделей, которая обладала бы наибольшей прогностической силой.

 

Почему мы используем аналогию портфельной оптимизации с методами машинного обучения  — Bag, Boost?! Потому что в действительности (и мы это продемонстрируем) нам абсолютно не важно, насколько хорошо динамику наших временных рядов прогнозируют «слабые» модели – нам важно только то, чтобы ошибки прогнозов наших моделей взаимно компенсировали бы друг друга в некотором интегральном смысле. Иными словами – в случае бустинга – ошибка прогноза линейной композиции была бы минимальной, а в случае портфельной оптимизации –  была бы минимальной ошибка прогноза нелинейной композиции (то есть самого портфеля).

( Читать дальше )

Книга, которая по праву может называться энциклопедией по инвестированию в долевые финансовые инструменты.
Упор делается на фундаментальный анализ и теорию инвестиционного портфеля Марковица, дополненную собственными модернизациями Шарпа.
Книга представляет   интерес для тех тех, кто готов пойти получать CFA, FRM, а также MBA (с углубленной частью в области управления активами и капиталом).
Для аналитиков профучастников рынка ценных бумаг и аналитиков управляющих компаний безусловно является настольной книгой.

Кто хочет найти в этой книге секреты торговли на фондовом рынке, тот будет разочарован. Это книга не для вас.
Это книга для тех, кто хочет понять глубинные причины ценообразования стоимости активов, мотивацию доверительных управляющих при ребалансировке инвестиционного портфеля.