SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. AlexeyPetrushin
Распределение вероятностей изменения цен, где Тяжелый Хвост?
- 05 января 2025, 14:07
- |
Есть гипотеза что изменения цен на акции описываются гибридным распределением — нормальным для головы, и парето для хвоста.
Распределение парето f(x) = Cx^-a можно увидеть на лог/лог графике как прямую линию.
Я построил эмпирическое распределение CDF, реальных цен на акцию, но не могу найти на нем «хвост», прямую линию, где она? (просто для сравнения я также построил нормальное распределение откалиброванное на тех же данных).
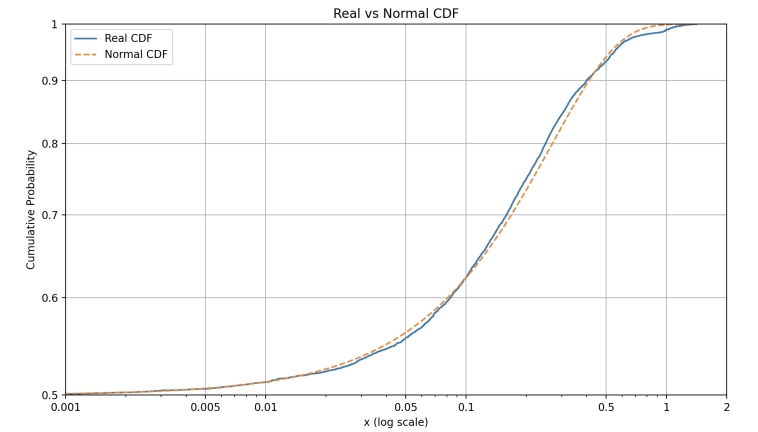
На графике показана только часть CDF, положительные измемения, в маштабле лог/лог. Также, изменения цен трансформированы, как: 1) лог траснформа и 2) отцентрированы относительно медианы. Нормальное распределение откалибровано на тех же трансформированных данных, с насильно принятым 0 взятым из медианы в качестве арифметического среднего (т.е. для нормального насильно поставлена медиана вместо арифметич среднего, так график лучше совпадает).
Данные — изменения цен на акцию, посчитаны как изменения за год, для каждого дня, diff_i=price_i/price_{i-360}, для цен одной акции за несколько десятилетий.
Вобщем, где на графике этот хвост? :)
АПДЕЙТ: Я неверно построил лог/лог график, нужно «перевернуть» график (комплементарную CDF построить, новый график снизу), тогда логарифмический масштаб гораздо лучше «растягивает» линию и она лучше видна (точнее то что никакой линии там нет). Видно что Нормальное Распределение недооценивает хвосты, и тяжелый хвост есть, но судя по всему не Парето, а что то послабее. Еще попробую варианты, и потом опубликую новые графики...

P.S.
В прошлых постах мне посоветовали посмотреть Обобщенное Гиперболическое Распределение (благодарность А. Г.). Я сомневался его использовать, поскольку там все таки не совсем Парето, но возможно оно реально хорошо подходит, попробую посмотрим...
Код и данные:
И данные скачать
Распределение парето f(x) = Cx^-a можно увидеть на лог/лог графике как прямую линию.
Я построил эмпирическое распределение CDF, реальных цен на акцию, но не могу найти на нем «хвост», прямую линию, где она? (просто для сравнения я также построил нормальное распределение откалиброванное на тех же данных).

На графике показана только часть CDF, положительные измемения, в маштабле лог/лог. Также, изменения цен трансформированы, как: 1) лог траснформа и 2) отцентрированы относительно медианы. Нормальное распределение откалибровано на тех же трансформированных данных, с насильно принятым 0 взятым из медианы в качестве арифметического среднего (т.е. для нормального насильно поставлена медиана вместо арифметич среднего, так график лучше совпадает).
Данные — изменения цен на акцию, посчитаны как изменения за год, для каждого дня, diff_i=price_i/price_{i-360}, для цен одной акции за несколько десятилетий.
Вобщем, где на графике этот хвост? :)
АПДЕЙТ: Я неверно построил лог/лог график, нужно «перевернуть» график (комплементарную CDF построить, новый график снизу), тогда логарифмический масштаб гораздо лучше «растягивает» линию и она лучше видна (точнее то что никакой линии там нет). Видно что Нормальное Распределение недооценивает хвосты, и тяжелый хвост есть, но судя по всему не Парето, а что то послабее. Еще попробую варианты, и потом опубликую новые графики...

P.S.
В прошлых постах мне посоветовали посмотреть Обобщенное Гиперболическое Распределение (благодарность А. Г.). Я сомневался его использовать, поскольку там все таки не совсем Парето, но возможно оно реально хорошо подходит, попробую посмотрим...
Код и данные:
import json
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
# Loading 'diffs.json'
with open('diffs.json', 'r') as file:
diffs = json.load(file)
# Log-transform the data
log_diffs = np.log(diffs)
# Calculate the center as median, it fits better than the mean
center = np.median(log_diffs)
# Center the log diffs
log_diffs_centered = log_diffs - center
# Function to fit a real CDF
def fit_cdf_(data):
sorted_data = np.sort(data)
n = len(data)
cdf = [(x, (i + 1) / n) for i, x in enumerate(sorted_data)]
return cdf
# Fitting real CDF
real_cdf = fit_cdf_(log_diffs_centered)
# Fitting normal CDF, forcing mean to be 0
variance = np.mean(log_diffs_centered**2) # Variance
sigma = np.sqrt(variance) # Standard deviation
# Extract CDF x-values
cdf_xs = np.array([x for x, _ in real_cdf])
# Compute the normal CDF for these x-values
normal_cdf = [(x, norm.cdf(x, loc=0, scale=sigma)) for x in cdf_xs]
# Plot real CDF and normal CDF
real_cdf_ys = [p for _, p in real_cdf]
normal_cdf_ys = [p for _, p in normal_cdf]
plt.figure(figsize=(8, 6))
plt.plot(cdf_xs, real_cdf_ys, label='Real CDF', linestyle='-')
plt.plot(cdf_xs, normal_cdf_ys, label='Normal CDF', linestyle='--')
plt.xscale('log') # Logarithmic x-axis scale
plt.yscale('log') # Logarithmic x-axis scale
plt.ylim(0.5, 1) # y-axis domain
plt.xlim(0.001, 2) # x-axis domain
plt.xlabel('x (log scale)')
plt.ylabel('Cumulative Probability')
plt.title('Real vs Normal CDF')
plt.legend()
x_ticks = [0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1, 2]
plt.xticks(x_ticks, [str(label) for label in x_ticks])
y_ticks = [0.5, 0.6, 0.7, 0.8, 0.9, 1]
plt.yticks(y_ticks, [str(label) for label in y_ticks])
plt.grid(True)
plt.show()И данные скачать
теги блога Alex Craft
- amd
- java
- Javascript
- microsoft
- portfolio
- python
- swift
- Uranium One
- usd
- акции
- алгоритм
- алготрейдинг
- анализ
- аналитика
- банки
- Беларусь
- бизнес
- Брокер
- брокеры
- валюта
- волатильность
- госдолг США
- данные
- деньги
- доллар
- доллар рубль
- игра
- ИИ
- иммиграция
- инвестирование
- инвестиции
- инсайдер
- инфляция
- инфляция в России
- инфляция в США
- искусственный интеллект
- исторические данные
- Келли
- макро
- макроэкономика
- Мандельброт
- математика
- мобильный пост
- модели
- модель
- монте-карло
- мудрость
- недвижимость
- Нелинейность рынка
- Нефть
- Новости
- оптимальный портфель
- оптимизация
- опцион
- опционы
- отчёт
- оффтоп
- парето
- перевод
- перевод денег
- плечи
- политика
- портфель
- портфель инвестора
- портфолио
- премиальные опционы
- прибыль
- прогноз
- программироание
- пут опцион
- пут опционы
- распределение
- Ребалансировка
- ресурсы
- рецензия на книгу
- риск
- робот
- рост
- рубль
- рынки
- рынок
- спекуляции
- статисика
- статистика
- стратегии
- США
- теория вероятностей
- теханализ
- торговые роботы
- трейдинг
- уран
- философия
- форекс
- фрактал
- фракталы
- хэдж
- шортсквиз
- экономика
- экономика США
- энергия



















UPD. кстати, в фильме предел риска — как раз описана ситуация, когда хвосты вдруг стали толстеть
Как вариант можно гистограмму (разбитие по корзинам) сделать, она сгладит.
По акции — это «средняя» акция, не самая спокойная, не самая волатильная, история несколько десятилетий, по идее, хвосты должны проявиться…
PS смотрю ваши ролики на ютубе, добротные
Вот эти как раз взяли это ведро черешни...
yandex.ru/video/preview/8007519925696137596
Самое интересное, что класс обобщенных гиперболических распределений — это класс распределений нормальных случайных величин со случайными средним и дисперсией и разными классами этих распределений. И в этом классе «лежит» почти все из распределений в справочниках по теорверу: и Хи-квадрат, и Лаплас и многое другое, кроме Парето.
rama.cont.perso.math.cnrs.fr/pdf/empirical.pdf
И еще нужно понимать как работает ЦПТ, желательно с нюансами, коих там много.
smart-lab.ru/blog/699507.php
Но это догадка конечно, сказать наверняка нельзя :)