SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Gusan
Откуда возникает улыбка волатильности?
- 17 августа 2013, 21:55
- |
Продолжая популярную сейчас тему с моделями улыбки волатильности, хочу поделиться результатами своего исследования на эту тему. Немного стремно делать это после поста Виталия Курбаковского. Но может кому-то и мое исследование будет интересно. Сам я не математик и не трейдер, просто программист. Поэтому не судите строго.
Наблюдая за поведением улыбки волатильности, уже давно мучали вопросы: Почему улыбка поднимается то вверх, то вниз? Почему она изогнута именно так, а не иначе? Почему перекатывается за текущей ценой БА, причем дно улыбки справа от БА и только к экспирации подтягивается к БА и улыбка становится симметричной? Почему ветви у нее то поднимаются, то опускаются? И главный вопрос: Что является причиной возникновения улыбки волатильности? В некоторых источниках утверждают, что улыбка возникает из-за толстых хвостов распределения приращений. Решил проверить это и провести небольшое исследование.
Насколько понял теорию вопроса, чтобы посчитать свою улыбку волатильности, нужно иметь распределение вероятностей, какой будет цена БА на экспирацию (в дальнейшем — распределение цен). Если знать это распределение, то можно однозначно вычислить цены опционов на каждом страйке, и потом, используя формулу Блека-Шоулза, можно вычислить IV на каждом страйке, и получить улыбку волатильности. Как можно получить распределение цен? Решил построить его, генерируя тысячи случайных траекторий цены, начиная с текущего значения БА. Конечные точки траекторий (цена БА на экспирацию) сохраняю, и в конце смотрю, как часто цена попадала в тот или иной диапазон. Так получаю распределение цен на экспирацию. Для построения случайной траектории решил использовать распределение приращений, которое реально было на рынке (в дальнейшем — эмпирическое распределение). Вот, например, распределение приращений (на минутках) для фьючерса RTS-9.11:
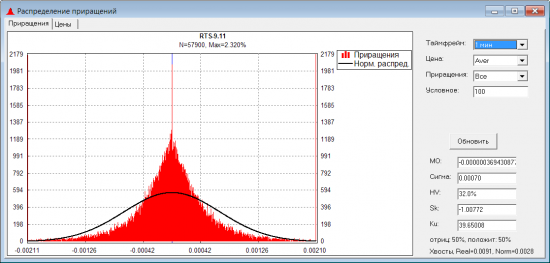
На гистограмму распределения реальных приращений наложен график плотности нормального распределения. Видно, что распределение реальных приращений отличается от нормального:
Может быть улыбка волатильности возникает именно из-за этих отличий эмпирического распределения от нормального? Проверим это. Построим распределение цен на экспирацию, используя эмпирическое распределение. Но сначала немного подкорректируем его. Дело в том, что в эмпирическом распределении уже заложен тренд, который был у БА за рассматриваемый период (например RTS-9.11 за выбранный период упал с 183505 до 161190). И если использовать исходное эмпирическое распределение, то матожидание распределения цен на экспирацию будет сильно отличаться от стартовой точки траекторий. Улыбку волатильности строить по такому распределению — нельзя. Поскольку не будет выполняться колл-пут паритет. И улыбки, посчитанные отдельно для путов и для коллов, не будут совпадать. Для выполнения паритета необходимо, чтобы матожидание распределения цен на экспирацию равнялось текущей цене БА (стартовому значению для всех траекторий). Исключим трендовую составляющую из приращений (как посоветовал broker25 в этом посте) и построим подкорректированное распределение цен на экспирацию:
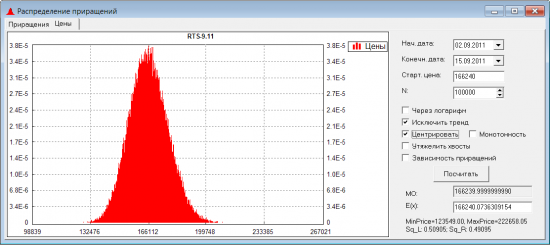
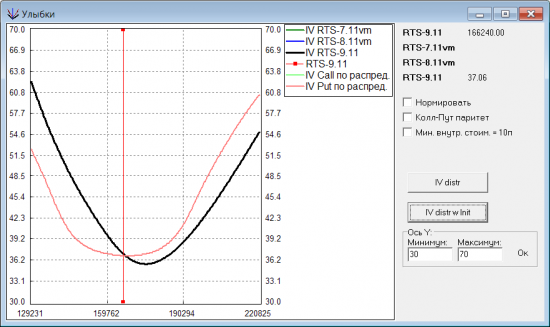
У этого распределения матожидание совпадает с текущим значением БА, поэтому можно рассчитывать улыбки. Посчитаем улыбку отдельно для путов и отдельно для коллов. Вот что получилось:
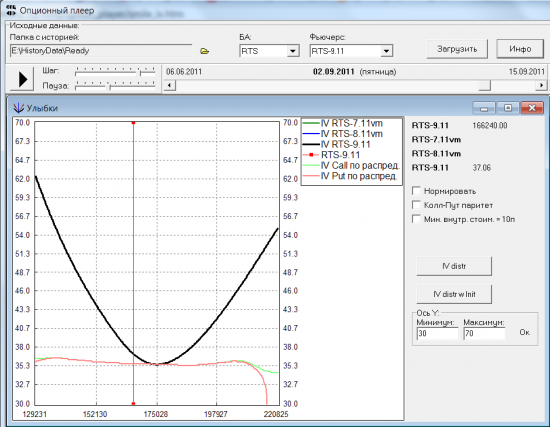
Черная жирная линия — улыбка волатильности, которую в тот момент транслировала биржа. Зеленая — улыбка волатильности, посчитанная по распределению цен для опционов колл. Розовая — улыбка волатильности для опционов пут.
Видно, что по краям посчитанные улыбки начинают расходиться, т.е. перестает выполняться колл-пут паритет. Но главное, посчитанные улыбки совсем не похожи на параболу. И напоминают скорее горизонтальную линию. Как же у биржевой улыбки получается парабола?
Здесь я долго бился, перепроверял расчеты, но все уточнения приводили к тому, что улыбка становилась все более похожей на горизонтальную линию. Пока не заметил, что в транслируемых биржей теор.ценах минимальная внутренняя стоимость опциона не бывает меньше 10п. Введя такую коррекцию, получил вот такую улыбку:
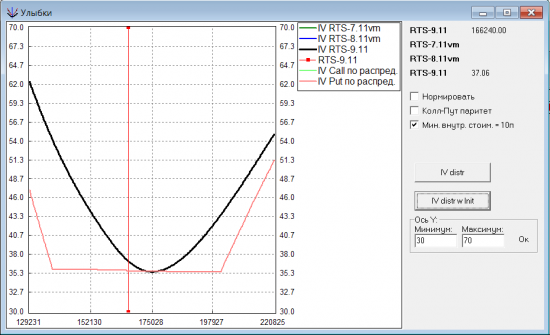
Это уже более похоже на биржевую улыбку. Но все равно смущает кусочно-линейная структура. Уберем коррекцию с 10п и искусственно «утяжелим» хвосты распределения цен так, чтобы это условие (внутренняя цена опциона >= 10п) выполнялось автоматически. Для такого распределения получаем вот такую улыбку:
Кажется, мы на верном пути и улыбка все ближе к биржевой. Вопрос только — как именно «утяжелить» хвосты у распределения цен? И почему собственно их нужно «утяжелять»? Ведь мы использовали распределение приращений, в котором и так хвосты были гораздо толще, чем у нормального распределения. Возможно, причина кроется в зависимости приращений. Когда мы строили очередную случайную траекторию движения БА к экспирации, то на каждом шаге очередное приращение выбиралось независимо от предыдущего. Т.е. мы исходили из принципа, что приращения в эмпирическом распределении независимы. Но так ли это в действительности?
Проведем эксперимент: после каждого значительного приращения (например, на +100п) запомним следующее приращение и посмотрим, какое получится распределение таких приращений. Вот какое условное распределение получается:
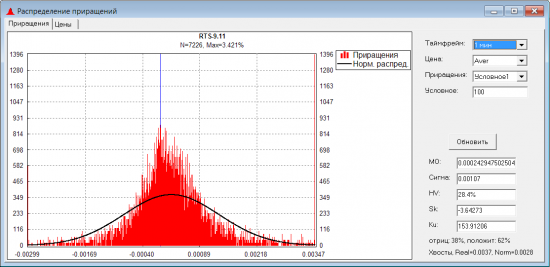
Видно, что матожидание этого распределения не ноль (0.02% от цены БА) и 60% приращений имеют положительные значения. Т.е. в 60% случаев после роста вверх на 100п и более, на следующем баре движение вверх продолжалось и в среднем было примерно 30-40п (скальперам — на заметку!). Т.е. наш экспресс-анализ показывает, что приращения нельзя считать независимыми. И для генерации случайной траектории движения цены нужно не просто случайно выбирать очередное приращение, а использовать при этом некие зависимости.
Попробуем сымитировать такие зависимости. Например, рассмотрим такой вариант: в 98% траектории строятся абсолютно случайно, в 1% траектория строится случайно, но с тенденцией к падению, в 1% — к росту. Вот какое распределение цен получается:
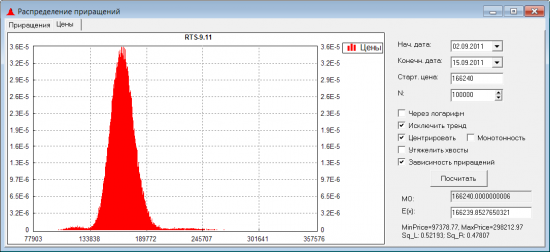
Для такого распределения получается следующая улыбка волатильности:
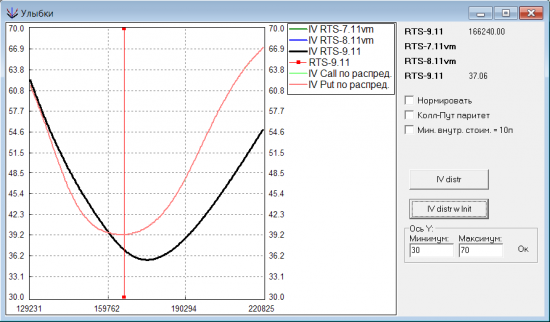
Форма улыбки все ближе к биржевой. Разберемся теперь с дном улыбки. У транслируемой биржей улыбки дно находится справа от текущего значения БА, и по мере приближения к экспирации, подтягивается к БА. И в последний день улыбка становится наконец симметричной. С чем связано такое поведение улыбки? Тут помог Олег Мубаракшин:
За смещение дна отвечает корреляция между ценой и волатильностью. То что мы наблюдаем для опционов на индекс — следствие отрицательной корреляции между приращениями цены фьючерса и приращениями его волатильности...
Попробуем смоделировать это. Т.е. будем использовать не фиксированное распределение приращений, а динамически меняющееся, в зависимости от того: растет текущая траектория цены или падает. Если растет, будем постепенно снижать волатильность. Если падает — будем повышать волу. Вот какое распределение цен получается при таком моделировании:
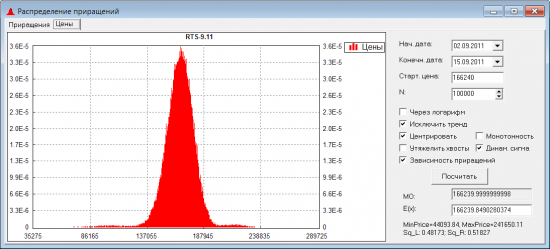
Видно, что теперь левая сторона распределения более растянутая, поскольку для ее построения использовалось более волатильное распределение приращений. Посмотрим теперь на улыбку, которая получается при таком распределении цен:
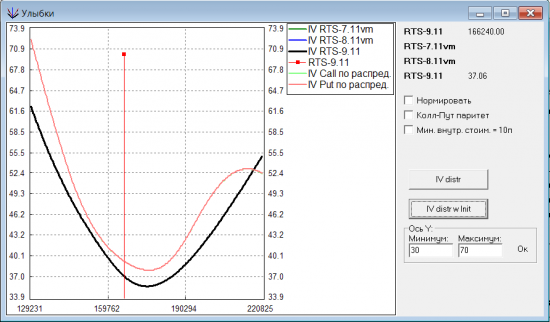
У улыбки справа возникла небольшая загогулина, видимо, у распределения цен справа недостаточно толстый хвост получился. Но главное, что утверждение Олега подтвердилось! Дно действительно сместилось вправо. Если посмотреть в динамике, то дно у такой улыбки будет также, как и у биржевой по мере приближения к экспирации подтягиваться к БА.
Итак, вот ответы на исходные вопросы:
Вот такое исследование и такие выводы получились. Буду рад любой критике или новым идеям.
Наблюдая за поведением улыбки волатильности, уже давно мучали вопросы: Почему улыбка поднимается то вверх, то вниз? Почему она изогнута именно так, а не иначе? Почему перекатывается за текущей ценой БА, причем дно улыбки справа от БА и только к экспирации подтягивается к БА и улыбка становится симметричной? Почему ветви у нее то поднимаются, то опускаются? И главный вопрос: Что является причиной возникновения улыбки волатильности? В некоторых источниках утверждают, что улыбка возникает из-за толстых хвостов распределения приращений. Решил проверить это и провести небольшое исследование.
Насколько понял теорию вопроса, чтобы посчитать свою улыбку волатильности, нужно иметь распределение вероятностей, какой будет цена БА на экспирацию (в дальнейшем — распределение цен). Если знать это распределение, то можно однозначно вычислить цены опционов на каждом страйке, и потом, используя формулу Блека-Шоулза, можно вычислить IV на каждом страйке, и получить улыбку волатильности. Как можно получить распределение цен? Решил построить его, генерируя тысячи случайных траекторий цены, начиная с текущего значения БА. Конечные точки траекторий (цена БА на экспирацию) сохраняю, и в конце смотрю, как часто цена попадала в тот или иной диапазон. Так получаю распределение цен на экспирацию. Для построения случайной траектории решил использовать распределение приращений, которое реально было на рынке (в дальнейшем — эмпирическое распределение). Вот, например, распределение приращений (на минутках) для фьючерса RTS-9.11:

На гистограмму распределения реальных приращений наложен график плотности нормального распределения. Видно, что распределение реальных приращений отличается от нормального:
- Вероятность незначительных изменений цены больше, чем в нормальном распределении;
- Вероятность средних изменений цены меньше, чем в нормальном;
- Вероятность значительных изменений цены больше, чем в нормальном (площадь под хвостами +-3*сигмы у эмпирического распределения в три раза больше чем у нормального);
Может быть улыбка волатильности возникает именно из-за этих отличий эмпирического распределения от нормального? Проверим это. Построим распределение цен на экспирацию, используя эмпирическое распределение. Но сначала немного подкорректируем его. Дело в том, что в эмпирическом распределении уже заложен тренд, который был у БА за рассматриваемый период (например RTS-9.11 за выбранный период упал с 183505 до 161190). И если использовать исходное эмпирическое распределение, то матожидание распределения цен на экспирацию будет сильно отличаться от стартовой точки траекторий. Улыбку волатильности строить по такому распределению — нельзя. Поскольку не будет выполняться колл-пут паритет. И улыбки, посчитанные отдельно для путов и для коллов, не будут совпадать. Для выполнения паритета необходимо, чтобы матожидание распределения цен на экспирацию равнялось текущей цене БА (стартовому значению для всех траекторий). Исключим трендовую составляющую из приращений (как посоветовал broker25 в этом посте) и построим подкорректированное распределение цен на экспирацию:

У этого распределения матожидание совпадает с текущим значением БА, поэтому можно рассчитывать улыбки. Посчитаем улыбку отдельно для путов и отдельно для коллов. Вот что получилось:

Черная жирная линия — улыбка волатильности, которую в тот момент транслировала биржа. Зеленая — улыбка волатильности, посчитанная по распределению цен для опционов колл. Розовая — улыбка волатильности для опционов пут.
Видно, что по краям посчитанные улыбки начинают расходиться, т.е. перестает выполняться колл-пут паритет. Но главное, посчитанные улыбки совсем не похожи на параболу. И напоминают скорее горизонтальную линию. Как же у биржевой улыбки получается парабола?
Здесь я долго бился, перепроверял расчеты, но все уточнения приводили к тому, что улыбка становилась все более похожей на горизонтальную линию. Пока не заметил, что в транслируемых биржей теор.ценах минимальная внутренняя стоимость опциона не бывает меньше 10п. Введя такую коррекцию, получил вот такую улыбку:

Это уже более похоже на биржевую улыбку. Но все равно смущает кусочно-линейная структура. Уберем коррекцию с 10п и искусственно «утяжелим» хвосты распределения цен так, чтобы это условие (внутренняя цена опциона >= 10п) выполнялось автоматически. Для такого распределения получаем вот такую улыбку:

Кажется, мы на верном пути и улыбка все ближе к биржевой. Вопрос только — как именно «утяжелить» хвосты у распределения цен? И почему собственно их нужно «утяжелять»? Ведь мы использовали распределение приращений, в котором и так хвосты были гораздо толще, чем у нормального распределения. Возможно, причина кроется в зависимости приращений. Когда мы строили очередную случайную траекторию движения БА к экспирации, то на каждом шаге очередное приращение выбиралось независимо от предыдущего. Т.е. мы исходили из принципа, что приращения в эмпирическом распределении независимы. Но так ли это в действительности?
Проведем эксперимент: после каждого значительного приращения (например, на +100п) запомним следующее приращение и посмотрим, какое получится распределение таких приращений. Вот какое условное распределение получается:

Видно, что матожидание этого распределения не ноль (0.02% от цены БА) и 60% приращений имеют положительные значения. Т.е. в 60% случаев после роста вверх на 100п и более, на следующем баре движение вверх продолжалось и в среднем было примерно 30-40п (скальперам — на заметку!). Т.е. наш экспресс-анализ показывает, что приращения нельзя считать независимыми. И для генерации случайной траектории движения цены нужно не просто случайно выбирать очередное приращение, а использовать при этом некие зависимости.
Попробуем сымитировать такие зависимости. Например, рассмотрим такой вариант: в 98% траектории строятся абсолютно случайно, в 1% траектория строится случайно, но с тенденцией к падению, в 1% — к росту. Вот какое распределение цен получается:

Для такого распределения получается следующая улыбка волатильности:

Форма улыбки все ближе к биржевой. Разберемся теперь с дном улыбки. У транслируемой биржей улыбки дно находится справа от текущего значения БА, и по мере приближения к экспирации, подтягивается к БА. И в последний день улыбка становится наконец симметричной. С чем связано такое поведение улыбки? Тут помог Олег Мубаракшин:
За смещение дна отвечает корреляция между ценой и волатильностью. То что мы наблюдаем для опционов на индекс — следствие отрицательной корреляции между приращениями цены фьючерса и приращениями его волатильности...
Попробуем смоделировать это. Т.е. будем использовать не фиксированное распределение приращений, а динамически меняющееся, в зависимости от того: растет текущая траектория цены или падает. Если растет, будем постепенно снижать волатильность. Если падает — будем повышать волу. Вот какое распределение цен получается при таком моделировании:

Видно, что теперь левая сторона распределения более растянутая, поскольку для ее построения использовалось более волатильное распределение приращений. Посмотрим теперь на улыбку, которая получается при таком распределении цен:

У улыбки справа возникла небольшая загогулина, видимо, у распределения цен справа недостаточно толстый хвост получился. Но главное, что утверждение Олега подтвердилось! Дно действительно сместилось вправо. Если посмотреть в динамике, то дно у такой улыбки будет также, как и у биржевой по мере приближения к экспирации подтягиваться к БА.
Итак, вот ответы на исходные вопросы:
- Отличие эмпирического распределения приращений от нормального и его толстые хвосты не является причиной возникновения улыбки.
- Улыбка возникает из-за толстых хвостов распределения цен на экспирацию.
- Скорее всего, эти толстые хвосты возникают из-за зависимости приращений в эмпирическом распределении.
- Вертикальное положение улыбки зависит от сигмы распределения приращений: распределение с большей сигмой будет поднимать улыбку вертикально вверх, с меньшей — опускать вниз.
- Наклон ветви улыбки зависит от «тяжести» хвоста распределения цен: чем «тяжелее» хвост, тем больше угол наклона соответствующей ветви улыбки.
- Смещение дна улыбки вправо связано с отрицательной корреляцией между ценой БА и его волатильностью.
Вот такое исследование и такие выводы получились. Буду рад любой критике или новым идеям.



















короче говоря, форма улыбки зависит от моментов распределения.
насчет зависимостей приращений и гэпов это уже труднее сказать — слишком далеко от Б-Ш
смысл построения своей улыбки?
мне очень многие доказывали что это прямо жизненно необходимо, но никто так и не смог доказать её практической ценности (
мож тут народ сможет?
предпоследний абзац в smart-lab.ru/blog/135825.php#comment1989176, более исчерпывающе —
smart-lab.ru/blog/135825.php#comment1990983
Все остальное — рефлексия, чтобы синтетический пут не выглядел слишком привлекательным. Строится из спроса на пут плюс некоторая пипсовая премия.
Поскольку опционные позиции у нас не рейтингуют, то и БШ никто не прльзуется. Смотрят «дойдет/не дйдет» просто.
Так что дефект в рассуждениях у вас где-то…
Если строить улыбку через моделирование как предлагаю в статье, и использовать для построения тяжелых хвостов у распределения цен на экспу, например, инфу об ОИ на дальних страйках, то это будет учитывать мнение крупных участников рынка о вероятности дойти/не дойти до определенного страйка. Т.е. улыбка будет строиться с использованием мнения институционалов о рынке (возможных раскладах). А не чисто по формуле БШ. В чем дефект?
Есть данность (читай биржевая улыбка — цены совершенно конкретные и не важно что из себя представляет визуализация этих данных). Все свои операции ты производишь в этой самой данности. А если данность не меняется то какой смысл ее «понимать»? (данность это не уровень волы итд, а тот факт что есть тяжелын хвосты, нет паритета иногда итп)
А предсказать изменение данности таким методом нельзя.
В чем смысл всего этого? Все работают в одних и тех же обстоятельствах (читай биржа).
Вот, на вскидку, несколько причин, почему может понадобится своя модель улыбки:
1. Биржевая улыбка не всегда хорошо проходит через бид-аски в стаканах.
2. Те, кто верит в Кукла, могут посчитать, что маркет-мейкеры (совокупный Кукл) специально манипулируют улыбкой, чтобы на этом зарабатывать (а те, кто доверился этой улыбке, соответственно, будут терять деньги).
3. Если на рынке армагеддон, сплошные маржин-коллы, никого нет в стаканах, то транслируемая биржей улыбка может быть совсем неадекватной.
Это только мои предположения. Может и не прав.
1. Не понял
2. Но это всегда так! Когда бы ты не решил совершить сделку на другой стороне будет ММ со своей ценой.
3. А что плохого в этом случае в биржевой улыбке? Это значит что она очень даже неплохо отражает текущую ситуацию (ведь армагедон — это неадекватная ситуация).
P.S. Я торгую опционами и искренне пытаюсь понять зачем может быть нужно моделировать свою улыбку.
1. Ну, например, в стакане конкретного страйка могут стоять бид-аск на уровне 20% IV, а биржа в этот момент транслирует улыбку, где на данном страйке IV, например, 21%.
2. Так чтобы не поддаваться на их манипуляции и нужна собственная улыбка.
3. Плохое то, что улыбка неадекватна и не отражает справедливости теоретических цен в этот момент. Вот, например, Никита Масюков как-то писал что их закрыли по маржин-колу именно из-за неадекватно перекошенной улыбки, хотя по его представлениям позиция была хорошей. Перекосило улыбку, так понимаю, именно из-за лавины маржин-колов. Когда позы закрывали по любым ценам. Если в такой момент иметь свою улыбку и видеть насколько несправедлива биржевая, то предполагаю можно хорошо заработать.
Но вообще, исходная цель исследования была не в практическом применении, а просто интересно стало — откуда появляется улыбка, захотелось лучше ее понять.
1. Так может биржа плохо считает улыбку? Которая фактически не отражает реального положения дел
2. Но тогда можно очень долго ждать подходящих условий. Если таковые возникнут вообще (а в опционах, вы же знаете, мне в некоторых случаях очень нало зайти перед выходными, или сразу после отчетов итд).
И опять же вход/выход будут на фоне все тех же манипуляций, так какая разница что они в принципе есть?
Едимнственный момент где это может быть полезным, это что бы «обнаружить» что манипуляции стали более агрессивными. Но тогда нужно определить что такое норма… а как это сделать я не представляю.
3. Вот именно! То что я пытаюсь выяснить. Можно цифрами играться хоть до посинения, но когда ты торгуешь реальными деньгами на реальном рынке, тебя закроют и все. Где же тогда смысл теоретизации?
Ладно, не буду вас больше мучать, я все же практик по натуре ) Но спасибо за дисскусию
1. Не то что плохо, но иногда косячит: forum.rts.micex.ru/viewtopic.asp?t=25632
2. Насчет нормы и ее обнаружения была у меня такая идея. Попробовать моделировать не одну улыбку, а несколько. С разной степенью агрессивности/консервативности у параметров. Получится диапазон улыбок. И попытаться найти такие параметры, чтобы в плеере биржевая улыбка двигалась внутри этого диапазона. Если такое получится сделать, то вот почти готовый котировальный робот: на нижней границе диапазона покупать волу, на верхней — продавать.
3. Ну их закрыли, насколько понимаю, из-за того что переборщили с ГО и не оставили себе запаса по прочности. Если бы запас был, то пересидели бы панику глядя на свою улыбку, а не на перекошенную биржевую.
Это касается ситуации, если поза уже открыта. Если же позы еще нет и случился перекос, то своя улыбка будет показывать на каких страйках можно будет открыться и ждать, пока биржевая нормализуется.
я присоединяюсь к твоему вопросу!
Вообще, в исследовании я не совсем верно сделал. Как базовое распределение приращений, я взял все приращения за квартал 06-09.2011, т.е. в это распределение попал всплеск волы в начале августа 2011г. Если бы брал приращения только скажем за последние одну-две недели, то сигма была бы поменьше и смоделированная улыбка была бы пониже. И когда «утяжелил» хвосты, то она как-раз поднялась бы до уровня биржевой. А не была бы выше, как у меня получилось в статье.
поскольку в конце был запрос на предложения — предложу автору исследовать теми же методами улыбку в период июль 2008 — июль 2009 — это очень интересно.
www.mirkin.ru/_docs/OAJ-2-2012.pdf
На каком временном окне считалась статистика?
Могу предположить, что если считать по минуткам, то окно будет дней тридцать.
Значит будет сильный лаг по времени. То есть мы будем опаздывать со своей улыбкой, на недельку другую.
Мне так кажется.
Вообще, возможно, необязательно использовать эмпирическое распределение приращений, и можно брать просто нормальное распределение. Все равно потом у распределения цен придется утяжелять хвосты и в первом и во втором случае. Тогда можно не мучиться выбором окна, а просто пересчитать заданный HV в сигму и получить базовое распределение приращений, по которому строить распределение цен и как-то потом ему утяжелять хвосты. Правда, для оценки текущего HV опять встанет вопрос выбора окна…
Если понять, откуда появляется улыбка — то вроде бы на основе исследования уже упоминавшегося broker25 был сделан вывод, что в ней ключевую роль играет непостоянство волатильности. Только не первой части исследования, на которую дана ссылка в тексте, а второй: smart-lab.ru/blog/124782.php.
Если же вам нужна своя модель улыбки — то ключевой вопрос: для чего именно? Исходя из того, что вы пишете ранее в этой дискуссии ( smart-lab.ru/blog/135825.php#comment1986904 ), изобретать объяснение «почему улыбка улыбится» вам не нужно в принципе. Все что требуется сделать — это взять какую-то параметризацию подходящей формы (да хоть биржевую же!) и самому написать фильтр Калмана или свою хрень аналогичной функциональности, которая будет подгибать 5-/6-параметрическую кривую под имеющиеся в рынке биды и оффера. То есть, воспроизвести то, что делает биржа, но на своей стороне и с возможностью в любой момент поправить параметры руками.
Дальше все, что нужно, это чтобы ваша программулина гнула качественно, то есть, не впадая в локальные минимумы, искала глобальный оптимум. Задача это весьма непростая (что видно из описываемых проблем биржевой кривой), но абсолютно никак не связана с вопросом «какова природа улыбки волатильности?». Чисто математико-инженерная задача — насколько хорошо придумаете и запрограммируете, настолько близкая к реальному рынку улыбка и будет.
Если же есть желание делать вокруг улыбки арбитраж, то есть, продавать то, что дороже вашей улыбки, и одновременно покупать то, что дешевле (Это, кстати, ответ Lexa83 и jest-trader, зачем нужна своя кривая), вам, наоборот, совершенно не нужна кривая, которая будет идеально описывать рынок. Ведь в этом случае вы никогда не найдете ни недооцененных, ни переоцененных опционов.
Поэтому для данного использования вам потребуется жесткая малопараметрическая кривая (например, описанная буквально на днях Виталием Курбаковским). Причем не факт, что даже при всего 3 параметрах вам все 3 имеет смысл менять, особенно часто. И это абсолютно другой вид деятельности и другая задача.
Мне правда было интересно — откуда появляется улыбка. Подспудно была мысль, что если удастся выяснить ее природу, то может получится и самому свою моделировать, но это была уже вторичная цель.
Когда broker25 написал первый пост, я был уже в середине своего исследования, и боролся с горизонтальной улыбкой — никак не мог понять как из нее сделать параболу. Из постов broker25 этого понять не смог, поэтому продолжил копать.
Насчет «в улыбке ключевую роль играет непостоянство волатильности». Сейчас попробовал у себя сгенерить улыбку где волатильность меняется (с падением БА — вола растет, с ростом БА — падает), но при этом чтобы приращения для построения траектории выбирались независимо друг от друга. Распределение цен на экспу получилось похожим на логнормальное, только наоборот: растянутый хвост слева, сжатый справа. А улыбка получилась просто линией с отрицательным наклоном, вместо параболы. Все-таки у меня получается, что ключевая роль в улыбке — это зависимость приращений. Именно это дает тяжелые хвосты, которые делают улыбку параболой. Или это неверный вывод?
когда волатильность меняется непрерывным образом, приращения по определению становятся зависимыми :) (не путать с «коррелированными»).
Касательно непостоянства волатильности — поиграйтесь с моделью Хестона ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C_%D0%A5%D0%B5%D1%81%D1%82%D0%BE%D0%BD%D0%B0
Сразу скажу, что она тоже далека от идеала, причем наиболее заметен ее недостаток на малых горизонтах до экспирации, поскольку изменяющаяся по броуновским приращениям волатильность не может сильно измениться за короткое время, а реально на рынке это иногда происходит. Тем не менее общую форму улыбки вы получите.
В википедии почему-то не приведена формула оценки опциона в явном виде — вообще она есть — если заинтересуетесь, нагуглите статью самого Heston, это 1994 год. Кстати, не удивлюсь, если в серьезных стат-мат пакетах эта формула зашита уже в готовом виде.
А как оцениваете такую идею: брать улыбку с рынка, получать из нее распределение вероятностей цен для каждого страйка (каким его видит сейчас рынок), потом (если есть собственное отличное мнение) вручную корректировать вероятности (прибавлять/уменьшать) на некоторых страйках, переводить подкорректированное распределение назад в улыбку и использовать ее для торговли? Возможно такое теоретически, и если да, то есть ли практический смысл в такой манипуляции?
«другое — изм. волы.»
Под волой имеется ввиду IV? Если да, то на каком-то конкретном страйке или сразу на всех (т.е. сколько страйков — столько и распределений изм. IV)? И за какой период (день/неделя/месяц/...) нужно взять эти изменения (цены и волы), чтобы перевести биржевую улыбку в распределение цен на экспу?
Но если копать дальше — есть более продвинутые модели. Есть даже разные ветки — арбитражные и безарбитражные модели. Надо четко понимать физический смысл этих формул, тогда все ясно становится. Но для реальной работы Хестона и стохастического прыжка должно быть достаточно. Я почти все рассказал))
Но в целом не могу сказать, что эта тема кого-то из наших трейдеров сильно заинтересовала.
Касаясь вашего предложения по использованию, выражу свое личное отношение. Я вообще, как мне кажется, довольно здраво оцениваю свои возможности (а точнее, невозможности) в области предсказания будущего движения базового актива. Поэтому предложенное вами для меня упирается не в математику, а в собственные способности произвести«собственное отличное мнение» по поводу, «более лучших»(©, Света-из-Иваново) вероятностей.
Если ваши силы в этом деле вызывают ваше же доверие — день на чтение статьи и выписывание формулы, 3 дня на программирование (с учетом графического интерфейса) — и со следующего понедельника вы готовы к бою :). Доказывать теорему Ферма по дороге не потребуется :)
broker25 вот здесь упоминал статью Агапова в ФиО (NN 9-10 за 2009) в которой мог освещаться этот вопрос. Это ваша статья? Если да, и там было про такое обратное конвертирование — можно ли ее как-нибудь прочитать?
Повторюсь, сам факт, что плотность риск-нейтрального распределения равна второй производной цены (то есть, гамме) — это результат Breeden, Litzenberger-1978. Вот ссылка на их работу:
yadi.sk/d/048IF-3F89ARO
Я же аккуратно разобрался, что происходит, если распределение не во всех точках имеет плотность + как это все связано с улыбками и каким свойствам они, улыбки, должны обладать, чтобы из них можно было вытащить подразумеваемую функцию распределения.
Я сделал выжимку двух основных результатов из статьи (без доказательств) + обсуждения, чего мы фактически получили этими результатами. Вот она:
yadi.sk/d/pAk3gx4W89BAm
Вас интересует, видимо, Теорема 2.
Насчет — гнуть параметрическую кривую — это сомневаюсь. Во-первых, вряд ли у меня это получится лучше чем у биржи (вернее, совершенно точно у меня это будет хуже). Во-вторых, зачем, если можно просто взять мидмаркет (среднее между бид и аском)?
Пост Виталия Курбаковского перечитал несколько раз, но, к сожалению, так и не понял идею.
откройте в квике график RTSVX и посмотрите на дату 22.09.2011. Вол за 1 день выросла с 42 на открытии до выше, чем 100 на вечерке (вечерку, как я понимаю, вычистили из истории). Но даже за дневную сессию рост составил 46 пунктов волатильности!!! Или, к примеру, 08.08.2011 — тоже душевная свечка с 36 до 76 волатильности за день.
Так вот, обычно в такие моменты все маркет-мейкеры сваливают с рынка примерно после 10-15 пунктов прироста волатильности. И дальше их там просто нет! Соответственно, рынка как такового тоже нет. Биржевая улыбка колбасится в этом свободном пространстве, как хочет, середина бид-аск спреда — это тоже ноль информации вплоть до дельты коллов меньше нуля!
Хорошо, если позиции еще нет… А если она уже есть и ею нужно управлять?
В такой ситуации, конечно, можно ставить постоянную во всех страйках волатильность, но гораздо удобнее несколькими понятными параметрами задать некоторую форму кривой и твердо поставить ее где-то между бидами и офферами. Рынок еще на 5% сдвинулся — поменял 1-2 параметра и дальше работаешь.
Кстати, в такие моменты наклон рыночной кривой оказывается очень существенным из-за паники — поэтому константа плохой вариант. Ну, а руками каждый страйк задавать — это совсем жесть. А если страйков 100 или 200 будет — тоже придется каждый переставлять? Так это вы весь день только свою улыбку рисовать будете, а когда нарисуете, уже пора ее будет подвинуть куда-то :). Так что хотя бы та же биржевая кривая с фиксированными, задаваемыми пользователем параметрами (безо всякого авто-подгибания)- это парашют на случай отказа двигателя, если можно так выразиться. И опыт показывает, что на рынке иногда такое действительно происходит.
Задавать волу на каждом страйке — это, конечно, жесть. Но если поза только на одном-двух страйках и нужно «только день простоять да ночь продержаться» пока биржевая не стабилизируется, то может и этот вариант пригодился бы.
нет. На эту тему как раз Олег Мубаракшин ( smart-lab.ru/profile/OM77/ ) делал доклад на прошлом НОКе. Со временем доклада он не рассчитал, поэтому содержательные выводы оказались скомканы в самом конце, но есть собственно исходный текст исследования на его сайте:
quant-lab.com/research/beta-vs-delta.html
(возможно, придется глянуть и предыдущие пару постов, кажется, это ссылка — финальная часть с выводами; сама презентация на НОКе также есть на сайте Олега).
Но если говорить по сути, смысл здесь прост: улыбка сдвигается вместе с базовым активом, а значит, дельта Блэка-Шоулза не описывает адекватно изменение цены опциона. Во-первых, есть движение влево-вправо (из-за того, что форма улыбка в целом привязана к точке денег, а не к конкретному числу), а во-вторых — вверх или вниз в зависимости от знака самого движения (из-за отрицательной корреляции изменения волатильности с изменением базового актива). Если эти 2 эффекта не учитывать (то есть, использовать дельту Блэка-Шоулза), то в целом ваша дельта будет хуже компенсировать изменение цены опционной части портфеля — это как раз показывает исследование.
Поэтому все зависит от того, насколько тактика торговли дельта-нейтральна. В качестве «общей справки плюс-минус лапоть» дельта Блэка-Шоулза вполне сгодится. А вот для более тонких расчетов (если, к примеру, вы ровняете дельту раз в день) уже нужно использовать и форму самой улыбки (так как за счет нее у вас волатильность в страйке меняется при параллельном переносе улыбки вправо-влево), и коррелированность. Первое, кстати, учесть проще, поскольку никаких дополнительных оценок на истории делать не надо, но, как показывают тесты Олега, сама по себе эта дельта дает не лучший дельта-хедж, чем Блэк-Шоулз. Так что тут каждый для себя решает. В принципе, если дельту регулярно не ровнять, то нафига ее вообще вычислять по большому-то счету?
Прошлый НОК, кстати, показал, что таких позиционных опционщиков, для которых текущая дельта — абстрактное число в терминале, довольно много — они разве что грязью Олега не закидали, за то что он им своей «бесполезной» математикой мОзги напряг. Часть из них уже и в этой дискуссии успела отметиться, кстати («не будем показывать пальцем, но это был Слоненок» © ).
И если, допустим, опытным путем (методом тыка) установил, что для купленной волы нужно поддерживать немного отрицательную дельту (по БШ), для проданной — наоборот, то есть ли смысл использовать более сложный вариант Олега, или в этом случае особых преимуществ его вариант не даст?
смотрите за финрезом. Желание что-то улучшить появляется в тот момент, когда по всем вашим прикидкам вы должны были иметь прибыль, а вместо этого получили убыток :). После этого начинаешь разбираться: что я не учел и как это в следующий раз учесть?
Так что если, на ваш взгляд, дельта Блэка-Шоулза с вашими задачами справляется — то и нечего огород городить :).
и ваще математики очень забавные ребята и я их очень уважаю!
вот тока реально зарабатывать они похоже не будут никогда…
ИМХО и без обид )
а, к примеру, Курбаковский со своей командой, по вашему мнению, воздухом питаются последние 5 лет? :) А Каленкович?
1)Своя модель нужна в моменты, когда биржевая безбожно врет (это бывает и при кризисах разного рода, а иногда и на ровном месте)) для адекватной оценки текущего финансового результата и для получения возможности адекватного управления своей позицией.
2) Своя модель (вовсе не обязательно идеально аппроксимирующая биржевые стаканы) нужна в момент формирования позиции для получения статистического преимущества (с точки зрения этой самой своей модели))) и понимания за какой фин рез мы собственно собрались бороться.
3) Своя модель крайне необходима для правильного управления рисками позиции (биржевая модель «пытается бегать за стаканами» и не дает возможности для вменяемого хеджа)
Исправите? Добавите?
Могу еще такой гипотетический вариант добавить:
4) Модель может пригодится для прогонов стратегии в тестере. Прогонять только на истории, не дает такой уверенности, тем более она у нас короткая пока. Всего лишь два черных лебедя прилетало. А вот если бы можно было прогонять на смоделированных тыщах возможных траекторий БА, и стратегия показывала бы хороший шанс выигрыша и VaR, тут уже больше уверенности. Вот тогда бы пригодилась возможность строить для произвольной траектории БА модельную улыбку.
По п. 4 — очень осторожно отношусь к «ненастоящим» (смоделированным) данным. Поскольку тут «как повернул, так и вышло» -в смысле, что в модель генерации заложил, такие результаты и получил. Поэтому не то что бы вообще не согласен, но мой вердикт — очень долго думать и очень осторожно использовать в каждом случае :).
Хвосты утяжелял подгоняя, но буквально со второй-третьей попытки. Просто из общих соображений: такой-то процент случайных кривых пустил вниз с таким-то трендом, такой-то наверх. Т.е. сотен вариантов параметров просто в лоб не перебирал. И есть идея, как утяжелять вообще не подгоняя.
А что если попробовать цены на краях ограничить снизу не 10 пунктами, а MM_spread/2, где MM_spread — это спред маркет-мейкеров (можно взять ~100)? То есть предположить, что на краях никого нет кроме маркетосов, которые стоят заданным спредом. А поскольку они не могут встать ниже 0, то минимальная цена получается MM_spread/2.
Если научиться точно утяжелять хвосты, то наверное будет получаться парабола, которая будет вписываться в соответствующую кусочно-линейную улыбку. Интересно, что разница между улыбками с ограничением в 10п и в 50п — довольно большая. Но биржевая, по-моему, вписывается все-таки в улыбку с ограничением в 10п.
Основное мое замечание, которое драматическим образом влияет на ценность работы — это (как я уже говорил) то, что в результате генерирования траекторий вы получили не приближенное к реальности распределение на экспирацию, а нормальное распределение… и небольшие коррекции, которые вы делаете, не помогут тут.
По выводам.
«Итак, вот ответы на исходные вопросы:
Отличие эмпирического распределения приращений от нормального и его толстые хвосты не является причиной возникновения улыбки.
Улыбка возникает из-за толстых хвостов распределения цен на экспирацию.»
Распределение на экспирацию и историческое распределение — связанные вещи)
«Скорее всего, эти толстые хвосты возникают из-за зависимости приращений в эмпирическом распределении.»
Не только из-за этого. Там и автокорреляция волатильности и тп.
«Вертикальное положение улыбки зависит от сигмы распределения приращений: распределение с большей сигмой будет поднимать улыбку вертикально вверх, с меньшей — опускать вниз.
Наклон ветви улыбки зависит от «тяжести» хвоста распределения цен: чем «тяжелее» хвост, тем больше угол наклона соответствующей ветви улыбки.»
Это верно.
«Смещение дна улыбки вправо связано с отрицательной корреляцией между ценой БА и его волатильностью.» — полностью согласен с q-trader: это вызвано асимметрией распределения, которая в свою очередь может быть вызвана этим или другими факторами. Кстати, смещение улыбки вправо характерно для индексов и акций, а для валют она может быть симметрична, либо смещена влево (опционы на Si)
Вообще, какая-то подмена понятий у народа наблюдается. Причина образования улыбки (формально) — это то, что цены опционов в стакане и то, как их сводит в единую кривую биржа отличаются от цены опционов по модели БШ (по БШ была бы константа). Причина того, что цены отличаются от модели БШ вообще в другой плоскости — это реальный рынок, здесь цена определяется спросом и предложением, и не должна следовать никаким моделям! Другое дело, что те, кто следуют более совершенным моделям оценки опционов, по идее, должны быть в выигрыше по сравнению с теми, кто основывается на заведомо грубых моделях. И если вы хотите, например, понять, как цену опционов считают количественные аналитики крупных западных маркетмейкеров, которые определяют рынок и статистически в плюсе — это требует очень долгого изучения и глубокого понимания опционной теории. Оно вам точно надо?..) Впрочем, если нравится и интересно — это отличный мотивирующий фактор, вся наука так и движется) А так да, хорошо бы уметь строить подразумеваемое распределение, умнейшие люди этим занимаются…
Здесь уже невооруженным глазом видно, что на нормальное оно совсем не похоже. Скорее — логнормальное. Как это и предполагается в теории БШ. Хотя для его построения использовалось эмпирическое распределение приращений (первая картинка в статье), а не нормальное.
Насчет нормального — я не совсем корректно выразился, сейчас попробую пояснить. Как я уже говорил, нормальное (или логнормальное) получается у вас при генерации случайных траекторий. Далее вы вносите поправки, которые, конечно же, меняют его и приближают к реальному. Но, на мой взгляд, приближают слишком грубо. Да, появляется асимметрия, но еще с реальным распределением должны совпадать моменты более высоких порядков (эксцесс).
Я сам примерно похожими вещами занимался… пока хватало энтузиазма)
Такая рекомендация/просьба от имени общественности: попробуйте вытащить из исторических данных распределение недельных приращений и построить по ним кривую волатильности для опционов на индекс за неделю до экспирации. Вместо фьючерса возьмите значение индекса (RTSI)
Насчет другого таймфрейма для приращений, я пробовал такие: 1мин, 5, 15, 30мин, 1час. Они все показывают примерно одну картину. Форма распределения приращений — очень похожа. HV практически одинаковые (плюс-минус процент). На дневках тоже примерно также, но их мало за квартал. И распределение приращений выглядит слишком разреженным и случайным. Если брать недели, то совсем мало приращений будет. Да и цель-то какая?
Вы сделали в целом верные и важные выводы, и может, теперь захотите пойти дальше в своей работе. Сообществу трейдеров было бы интересно ознакомиться с ее результатами! Не так много у нас людей, кто на серьезном уровне этим занимается и делится результатами.
Но если ваша цель состояла только в том, чтобы понять, откуда возникает улыбка и что влияет на ее характеристики, то для этого не обязательно было проводить собственное исследование, можно было просто почитать литературу) Впрочем, эта литература в основном на английском.
"...в реальной жизни значительные изменения цены наблюдаются чаще, чем предсказывает нормальное распределение...".
Оказалось, что причина в другом.
Хотел даже плюсик в профиль поставить — оказалось, что уже))))
Зная внутреннюю динамику процесса, можно понять гораздо больше.
И эффективнее использовать явление на макроуровне.
Спасибо искреннее за исследование! Респект!
Правда, мне так и не удалось смоделировать улыбку так, чтобы это не противоречило поведению БА и волы на истории. Одним только случайным блужданием цены, пусть даже с динамически изменяющейся волатильностью — улыбку не получить, нет толстых хвостов у получающегося распределения цен. Видимо, для толстых хвостов нужно вводить в модель какие-то внешние воздействия на цену, типа как это было 3 марта.
Я стараюсь не лезть в Познание Мира глубже, чем необходимо для «нормальной жизни» (это не относится к вещам, которые мне 'очень интересны'). Я, например, как Шерлок, отец его Конан Дойль, Холмс — могу не знать вещей порядка «Земля вращается вокруг Солнца, а не наоборот» ( был такой эпизод:) )
А по поводу «так и не удалось смоделировать улыбку так, чтобы это не противоречило поведению БА и волы на истории» — Ты пытаешься подогнать (свой) алгоритм через RV (=HV), а у Биржи алгоритм «упреждающий». Не? Или я не вполне вник? Или у Тебя есть потиковая история 'всего, чего надо' на исследуемом периоде? Поясни.
И ещё.
Из всех тонн макулатуры про и по теме торговли — и с точки зрения «математиков», и с точки зрения «логиков», и с т.з. «практиков» (сам я «Логик») — я уловил мысль, что по отношению к приращениям при движении актива (я, кст, не считаю эти приращения чисто 'случайными'), корректнее использовать не 'нормальное распределение', а 'логнормальное'. Может, я не в тему, но может стоит попробовать))))
В своё время эта идея ('логнормаль') настолько хорошо вписалась в моё вИдение мира описания фин.активов, что я даже ув. А.Г. пытался советы давать)))) (щя если найду — ссылку на обсуждение скину).
За сим «кувшин моих мыслей показывает дно»))))
smart-lab.ru/blog/156383.php#comment2270017
и далее
А нафига вообще отстраивать «свою» улыбку?
На арбитраже улыбки (имхо) кучу денег не сделать. Комиссии большие, гигантским объёмом не войдёшь, а перекосы зачастую буквально в несколько долей процента…
Или я и тут неправ?))
На НОК-7 был очень интересный доклад Олега Мубаракшина quant-lab.com/. Он рассказывал про свою модель улыбки. Насколько я понял, он является маркет-мейкером ОЛМы и использует свою модель при котировании опционов на валюту. И ОЛМА является одним из самых крупных ММ на нашем рынке.
Так что, думаю все-таки своя улыбка — полезная вещь. Не только с теоретической точки зрения (лучше понимать рынок), но и с практической.
Насчет нормаль/логнормаль. Есть два разных распределения:
1. Распределение приращений.
2. Распределение цен на экспирацию.
По теории БШ если для первого распределения взять нормальное, то второе получится логнормальным.
Буду учитывать их при торговле.
Этим общение и полезно))))