SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. broker25
Рисуем улыбку с помощью дельта-хеджа
- 19 декабря 2013, 13:16
- |
Продолжаю заумные, бесполезные и оторванные от жизни теоретические изыскания)) В этой статье я еще сильнее запутаю вопрос о улыбке опционов, наведу тень на плетень, запудрю мозги и напущу тумана))) Я покажу, что вопрос о форме улыбки еще сложнее, чем кажется тем, кто думает, что он сложный. В общем, я честно предупредил. Те, кто не хотят себя мучить, могут сразу перейти к выводам. Дисклеймер закончен, задержите дыхание — ныряем!
В последней статье «Улыбка недельных опционов» я вывел теоретическую улыбку на основании эмпирического распределения приращений индекса РТС. Является ли выведенная улыбка «справедливой»? Чтобы это проверить, нарисуем улыбку альтернативным способом — с помощью дельта-хеджа.
Также используем эмпирическое распределение пятидневных скачков базового актива. В качестве базового актива возьмем склеенный фьючерс на индекс РТС. Напомню, в прошлой статье базовым активом служил сам индекс. Здесь я использую дельта-хедж, хеджировать индекс нельзя, приходится использовать фьючерс. На результате, как будет видно далее, эта замена скажется не сильно.
Техника эксперимента повторяет изложенную ранее. Есть скользящее окно, бегающее с января 2010г. по февраль 2013г. и определяющее начальный день и день экспирации. Время до экспирации – пять дней. Все доходности скорректированы на тренд, и матожидание среднего скачка равно единице.
По сути у нас имеется ряд скачков базового актива, определяющий его эмпирическое распределение. Неважно, что выбрать в качестве начальной точки каждого эксперимента. Примем в качестве начальной точки – 150000 пунктов. Цена до экспирации прыгает так, чтобы доходность повторяла историческую доходность соответствующих дней.
Как и в предыдущей статье, будем искать волатильность страйка в виде смайла, где смайл определяется относительно известной центральной IV квартальных опционов по формуле:
Волатильность страйка i = IV(0) + смайл(i) (1)
Решение задачи – смайл, дающий наилучшую начальную цену опциона. Для данного страйка этот смайл минимизирует сумму ошибок: квадратов разности начальных теоретических цен и реализованного дохода от опционов. Возьмем корень из этой величины, чтобы не было страшных триллионов. Получим функционал для минимизации.
Как считается реализованный доход от опциона? Это сумма дохода от дельта-хеджа и стоимости опциона на экспирации.
Что такое начальная теоретическая цена опциона? Это стоимость опциона по БШ, где в качестве волатильности подставляется правая часть формулы (1) с выбранным смайлом. Лучший смайл определяется простым перебором.
Каждый эксперимент длится пять дней. Каждый день, кроме последнего выравнивается дельта. Для простоты и большей точности будем считать, что базовый актив бесконечно делим, так что дельта обнуляется полностью. Возникает вопрос: как считать дельту. Способов расчета дельты несколько.
Согласно первому способу, в начале каждого эксперимента волатильность фиксируется на уровне (IV(0) + смайл), и хедж производится с одной волатильностью до соответствующей экспирации.
Согласно второму способу, фиксируется только смайл, но волатильность меняется: подставляется IV центрального страйка на соответствующую дату.
Согласно третьему способу, смайл не учитывается, подставляется только волатильность на соответствующую дату.
Добавим еще четвертый способ, где волатильность считается в абсолютных числах, а не по отношению к IV(0), и фиксирована до экспирации. Результаты сравнения разных способов указаны в табличке.
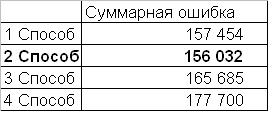
Наилучшим способом считаем тот, который минимизирует суммарную ошибку по всем страйкам. Как видно из таблички выше, лучший способ второй, с меняющейся волатильностью. Посчитанные этим способом смайлы представлены ниже
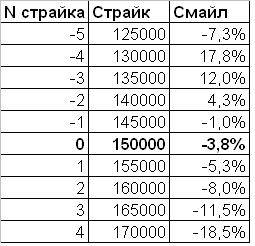
Эксперименты показали, что расчетная волатильность у крайних страйков сильно меняется в зависимости от способа дельта-хеджа. Очевидно это связано с тем, что недель, в которые базовый актив прыгает сильно, мало, и данных для надежной статистики недостаточно. Обрежем крайний слева страйк и крайний справа страйк.
Теперь сравним смайлы, полученные вторым способом, и смайлы, выведенные в предыдущей статье методом без хеджа для индекса РТС. Для большей убедительности добавим к графику смайлы, расчитанные вторым способом, где базовым активом выбран тоже индекс, а не фьючерс. Разместим также на графике реальные рыночные улыбки за 10.12.2012г. и 8.12.11г. за неделю до экспирации.
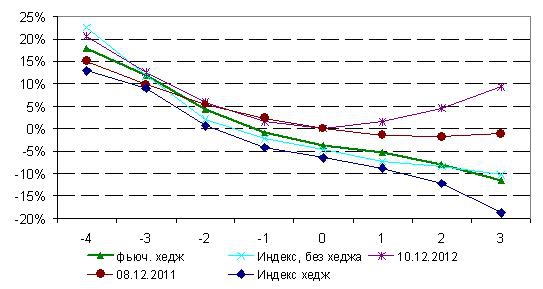
Какие выводы можно сделать из картинки выше? Улыбки, выведенные тремя способами с помощью эмпирического распределения, похожи. Справа от центрального страйка загиба вверх не наблюдается. Относительно левой части графиков трудно однозначно сказать, завышены или занижены рыночные цены опционов. Что касается центральной и правой частей графика, то вывод здесь однозначен — рыночная IV задрана вверх и опционы переоценены. Вывод выглядит спорно. Тем не менее, напомню, что он сделан именно для недельных опционов. Картина для других периодов может серьезно отличаться.
P.S. Заинтересован в работе, связанной с опционами. Пишите в личку.
В последней статье «Улыбка недельных опционов» я вывел теоретическую улыбку на основании эмпирического распределения приращений индекса РТС. Является ли выведенная улыбка «справедливой»? Чтобы это проверить, нарисуем улыбку альтернативным способом — с помощью дельта-хеджа.
Также используем эмпирическое распределение пятидневных скачков базового актива. В качестве базового актива возьмем склеенный фьючерс на индекс РТС. Напомню, в прошлой статье базовым активом служил сам индекс. Здесь я использую дельта-хедж, хеджировать индекс нельзя, приходится использовать фьючерс. На результате, как будет видно далее, эта замена скажется не сильно.
Техника эксперимента повторяет изложенную ранее. Есть скользящее окно, бегающее с января 2010г. по февраль 2013г. и определяющее начальный день и день экспирации. Время до экспирации – пять дней. Все доходности скорректированы на тренд, и матожидание среднего скачка равно единице.
По сути у нас имеется ряд скачков базового актива, определяющий его эмпирическое распределение. Неважно, что выбрать в качестве начальной точки каждого эксперимента. Примем в качестве начальной точки – 150000 пунктов. Цена до экспирации прыгает так, чтобы доходность повторяла историческую доходность соответствующих дней.
Как и в предыдущей статье, будем искать волатильность страйка в виде смайла, где смайл определяется относительно известной центральной IV квартальных опционов по формуле:
Волатильность страйка i = IV(0) + смайл(i) (1)
Решение задачи – смайл, дающий наилучшую начальную цену опциона. Для данного страйка этот смайл минимизирует сумму ошибок: квадратов разности начальных теоретических цен и реализованного дохода от опционов. Возьмем корень из этой величины, чтобы не было страшных триллионов. Получим функционал для минимизации.
Как считается реализованный доход от опциона? Это сумма дохода от дельта-хеджа и стоимости опциона на экспирации.
Что такое начальная теоретическая цена опциона? Это стоимость опциона по БШ, где в качестве волатильности подставляется правая часть формулы (1) с выбранным смайлом. Лучший смайл определяется простым перебором.
Каждый эксперимент длится пять дней. Каждый день, кроме последнего выравнивается дельта. Для простоты и большей точности будем считать, что базовый актив бесконечно делим, так что дельта обнуляется полностью. Возникает вопрос: как считать дельту. Способов расчета дельты несколько.
Согласно первому способу, в начале каждого эксперимента волатильность фиксируется на уровне (IV(0) + смайл), и хедж производится с одной волатильностью до соответствующей экспирации.
Согласно второму способу, фиксируется только смайл, но волатильность меняется: подставляется IV центрального страйка на соответствующую дату.
Согласно третьему способу, смайл не учитывается, подставляется только волатильность на соответствующую дату.
Добавим еще четвертый способ, где волатильность считается в абсолютных числах, а не по отношению к IV(0), и фиксирована до экспирации. Результаты сравнения разных способов указаны в табличке.

Наилучшим способом считаем тот, который минимизирует суммарную ошибку по всем страйкам. Как видно из таблички выше, лучший способ второй, с меняющейся волатильностью. Посчитанные этим способом смайлы представлены ниже

Эксперименты показали, что расчетная волатильность у крайних страйков сильно меняется в зависимости от способа дельта-хеджа. Очевидно это связано с тем, что недель, в которые базовый актив прыгает сильно, мало, и данных для надежной статистики недостаточно. Обрежем крайний слева страйк и крайний справа страйк.
Теперь сравним смайлы, полученные вторым способом, и смайлы, выведенные в предыдущей статье методом без хеджа для индекса РТС. Для большей убедительности добавим к графику смайлы, расчитанные вторым способом, где базовым активом выбран тоже индекс, а не фьючерс. Разместим также на графике реальные рыночные улыбки за 10.12.2012г. и 8.12.11г. за неделю до экспирации.

Какие выводы можно сделать из картинки выше? Улыбки, выведенные тремя способами с помощью эмпирического распределения, похожи. Справа от центрального страйка загиба вверх не наблюдается. Относительно левой части графиков трудно однозначно сказать, завышены или занижены рыночные цены опционов. Что касается центральной и правой частей графика, то вывод здесь однозначен — рыночная IV задрана вверх и опционы переоценены. Вывод выглядит спорно. Тем не менее, напомню, что он сделан именно для недельных опционов. Картина для других периодов может серьезно отличаться.
P.S. Заинтересован в работе, связанной с опционами. Пишите в личку.
теги блога broker25
- HV
- IV
- KZOS
- NKNC
- акции
- акции США
- алготрейдинг
- бабочка
- Брокер
- бэктестинг
- бюджет
- волатильность
- вор
- ВТБ
- второй эшелон
- газ
- газеты
- Газпром
- дельта-хеджирование
- дефицит бюджета
- дивиденды
- железный кондор
- здоровье трейдера
- зигзаг
- Индексы
- Историческая волатильность
- Казаньоргсинтез
- Китай
- корреляция активов
- макро
- ММВБ
- мультипликаторы
- Навальный
- накопительная часть пенсии
- налоги
- НДФЛ
- Нефть
- Нижнекамскнефтехим
- НПФ
- обмен акций
- опцион волатильность
- опционные спреды
- Опционы
- офф-топ
- оффтоп
- оценка акций
- поводыри
- приватизация
- прогноз
- прогноз по акциям
- продажа опционов
- продажа путов
- расчет в рублях
- реструктуризация
- рецензия на книгу
- Роснефть
- российский рынок акций
- Рынок акций США
- Саудовская Аравия
- Сибур
- сила Сибири
- Сила Сибири-2
- система
- скачать
- смартлаб конкурс
- сравнительный анализ
- суд
- сырье
- тест
- тики
- толстые хвосты
- Тольяттиазот
- торговые роботы
- улыбка
- улыбка волатильности
- философия трейдинга
- финанализ
- ФНБ
- фундаментальный анализ
- фундаметальный анализ
- хеджирование
- экспорт газа
- эмиссия денег
- Яндекс



















Еще раз: что этот пост, что предыдущий — интересные.
Единственное не очень пойму математический смысл учета дельтахеджа и вообще корректность такого расчета.
Вот есть опцион. Его цена = мат ожидание прибыли по нему. Получили мат ожидание, получили волатильность. Это ясно.
Теперь добавим к опциону дельтахедж. Во-первых тут мы сразу подключаем Б-Ш, а при подсчете просто мат ожидания Б-Ш никак не учитывается. Вообщем, немного лень мне делать длинный комментарий, но посыл мой таков: что-то настораживает меня корректность такого расчета.
f1(x) = A
второй случай эквивалентен решению уравнения
f1(x) = f2(x) + A
Пусть f3(x) = f1 -f2
f3(х) = A.
Но замечание мое не в этом.