SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Gusan
Модель Хестона и гэпы
- 27 октября 2014, 04:30
- |
Обнаружил несколько ошибок в своем прошлом исследовании Откуда возникает улыбка волатильности. В этом посте хотел бы их исправить (чтоб не стирать старый, там все-таки много интересного в комментариях). А также предложить на критику новую версию — откуда возникает улыбка и от каких факторов зависит.
Одна из ошибок того исследования была в предположении, что существует некая инерция в движениях цены БА: чем больше очередное приращение цены, тем больше вероятность что следующее приращение продолжится в том же направлении. Именно добавление этого эффекта в модель давало толстые хвосты и изгиб улыбки параболой. Но более внимательный анализ истории показал, что этого эффекта не наблюдается. Каким бы большим не было приращение — матожидание следующего будет ровно 0.
Но главной ошибкой было использование эмпирического распределения приращений для построения распределения цен на экспу. Понять что это ошибка, помогла всего одна фраза от
Арсена Яковлева (не ручаюсь за точность, но суть вроде такая):
Исторический ряд не повторится в будущем и лишь показывает свойства процесса движения цены.
Если поверить этому утверждению (а я сразу поверил), то конечно же неправильно брать приращения, которые были на историческом ряде, и только с помощью их пытаться построить все возможные случайные траектории цены. Более правильно было бы выявить некоторые закономерности на истории, оформить это в виде процесса, и потом уже с его помощью генерировать множество возможных траекторий цены.
Посему решил воспользоваться советом Андрея Агапова и поиграться с моделью Хестона. Реализовал в силу своего разумения, проверил на отдельных траекториях цены/волы, чтобы присутствовали основные факторы модели: отрицательная корреляция между ценой и волой, стремление мгновенной волы БА возвращаться к заданному среднему значению с заданной скоростью, волатильность у траектории волы была равна заданной величине (VolOfVol). Все это присутствовало в отдельных траекториях, но в итоговом распределении не получилось толстых хвостов, и улыбка была просто наклонной прямой:
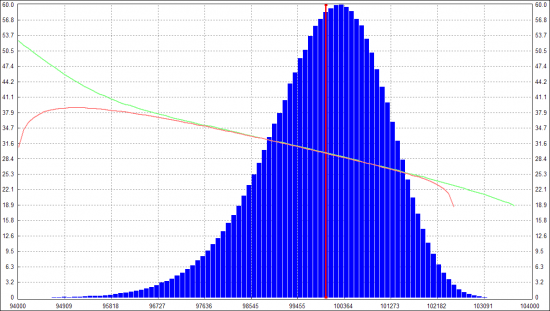
(зеленая линия — считаю по распределению цены колл и перевожу в IV по БШ; красная линия — тоже самое для путов; расхождение на хвостах — погрешность вычислений)
Кирилл Ильинский (во второй лекции), а также Unforgiven утверждали, что за изгиб улыбки в виде параболы отвечает VolOfVol. Но сколько не экспериментировал с этим параметром (даже делал его динамически меняющимся) — толстых хвостов не получалось и улыбка оставалась прямой.
Никита Масюков подсказал, что на изгиб улыбки может быть влияют прыжки цены. Попробовал смоделировать это так: с заданной вероятностью (небольшой) генерируется гэп, размер которого берется из нормального распределения, сигма которого в заданное кол-во раз больше сигмы, используемой во время обычного блуждания цены. Добавил это в модель и у полученного распределения появились толстые хвосты, правда изгиб у улыбки был очень слабенький. Тогда добавил такой эффект: если происходит гэп, то делаю взлет волы (не только для гэпа вниз, но и вверх тоже). И вот это уже хорошо загнуло улыбку в виде параболы:
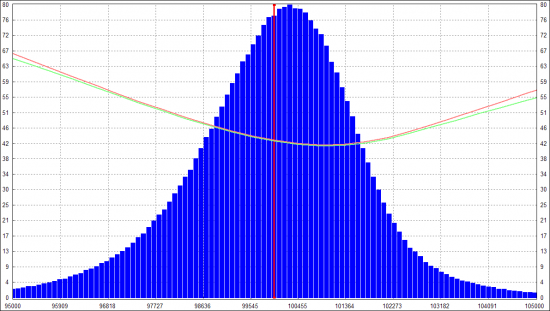
Тут бы успокоиться и просто порадоваться, что теперь примерно понятно откуда возникает улыбка. Но заметил проблему: IV на центре такой улыбки получался слишком большим. На картинке выше начальная вола БА = 30%, а IV на центре получилась 42-43%. В реале, насколько наблюдал, IV тоже выше чем HV, но все-таки не настолько. Если в модели снизить вероятность и размер гэпа, чтобы IV была только немного выше начальной волы, то улыбка становится почти плоской. Подсветить в чем проблема помогла HV-улыбка, на которую немного отвлекусь.
В какой-то момент захотелось проверить гипотезу, что улыбка IV показывает ожидание рынка — какая в среднем будет вола у БА, если цена придет на тот или иной страйк. Стал считать HV у каждой случайной траектории, и показывать это в виде облачка точек: по X финальная цена, куда пришла траектория на экспу, по Y — HV этой траектории. Вот что получилось для модели без гэпов:
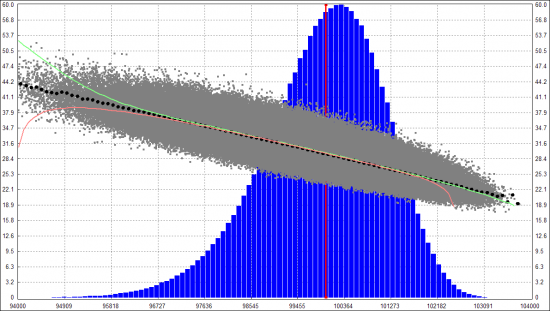
(черные кружочки — среднее HV на соответствующем участке, решил назвать это HV-улыбкой)
Видно что IV и HV улыбки очень хорошо совпали. Но вот если добавить гэпы (и на время убрать отрицательную корреляцию между БА и волой), то картина получается такая:
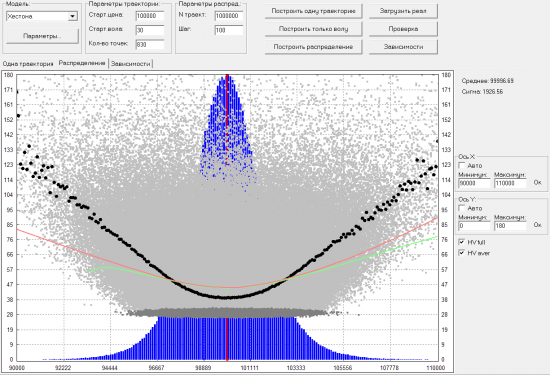
Здесь уже IV и HV плохо совпадают. Но главное видно почему поднимается улыбка IV при моделировании гэпов. В самом низу проглядывает горизонтальное облачко (точки темно-серого цвета), на уровне 30% (именно такая была стартовая вола у всех траекторий). Точки из этого облачка соответствуют траекториям в которых не было гэпа. А все точки выше него (светло-серого цвета) соответствуют траекториям, в которых был хотя бы один гэп. Получается что траектории с гэпами, которые возвращались к стартовому значению цены, имеют такую же высокую волу, как и те, которые унесло далеко в сторону. Из общих соображений, решил что это неправильно. Интуитивно хочется, чтобы облако HV траекторий с гэпами, было не равномерно рассеяно, а группировалось вокруг улыбки. Что-то вроде такой картинки:
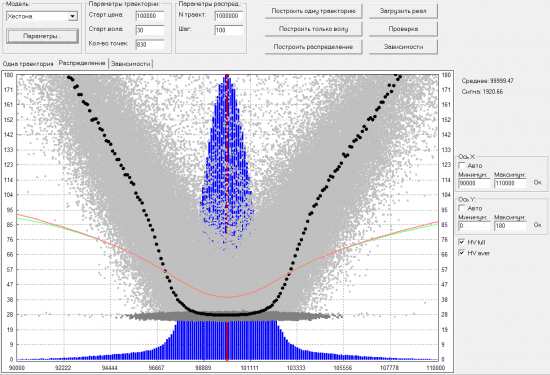
Но получил ее не совсем честным путем. А хотелось бы добавить что-то в модель, чтобы такая группировка получалась по-честному. Что-нибудь типа такого: если гэп в сторону от стартового значения цены, то идет рост волы, а если потом случается гэп в обратную сторону, то не увеличивать волу еще больше, а наоборот возвращать ее к стартовым значениям. Правда, пока не понимаю как это формализовать.
В общем, хотелось бы посоветоваться — в правильном ли направлении двигаюсь или уже занесло куда-то не туда. Допустимо ли добавлять в модель гэпы и всплески волы после них, или загиба улыбки в виде параболы можно было добиться одним VolOfVol и нужно искать ошибку в своей реализации модели Хестона?
Одна из ошибок того исследования была в предположении, что существует некая инерция в движениях цены БА: чем больше очередное приращение цены, тем больше вероятность что следующее приращение продолжится в том же направлении. Именно добавление этого эффекта в модель давало толстые хвосты и изгиб улыбки параболой. Но более внимательный анализ истории показал, что этого эффекта не наблюдается. Каким бы большим не было приращение — матожидание следующего будет ровно 0.
Но главной ошибкой было использование эмпирического распределения приращений для построения распределения цен на экспу. Понять что это ошибка, помогла всего одна фраза от
Арсена Яковлева (не ручаюсь за точность, но суть вроде такая):
Исторический ряд не повторится в будущем и лишь показывает свойства процесса движения цены.
Если поверить этому утверждению (а я сразу поверил), то конечно же неправильно брать приращения, которые были на историческом ряде, и только с помощью их пытаться построить все возможные случайные траектории цены. Более правильно было бы выявить некоторые закономерности на истории, оформить это в виде процесса, и потом уже с его помощью генерировать множество возможных траекторий цены.
Посему решил воспользоваться советом Андрея Агапова и поиграться с моделью Хестона. Реализовал в силу своего разумения, проверил на отдельных траекториях цены/волы, чтобы присутствовали основные факторы модели: отрицательная корреляция между ценой и волой, стремление мгновенной волы БА возвращаться к заданному среднему значению с заданной скоростью, волатильность у траектории волы была равна заданной величине (VolOfVol). Все это присутствовало в отдельных траекториях, но в итоговом распределении не получилось толстых хвостов, и улыбка была просто наклонной прямой:

(зеленая линия — считаю по распределению цены колл и перевожу в IV по БШ; красная линия — тоже самое для путов; расхождение на хвостах — погрешность вычислений)
Кирилл Ильинский (во второй лекции), а также Unforgiven утверждали, что за изгиб улыбки в виде параболы отвечает VolOfVol. Но сколько не экспериментировал с этим параметром (даже делал его динамически меняющимся) — толстых хвостов не получалось и улыбка оставалась прямой.
Никита Масюков подсказал, что на изгиб улыбки может быть влияют прыжки цены. Попробовал смоделировать это так: с заданной вероятностью (небольшой) генерируется гэп, размер которого берется из нормального распределения, сигма которого в заданное кол-во раз больше сигмы, используемой во время обычного блуждания цены. Добавил это в модель и у полученного распределения появились толстые хвосты, правда изгиб у улыбки был очень слабенький. Тогда добавил такой эффект: если происходит гэп, то делаю взлет волы (не только для гэпа вниз, но и вверх тоже). И вот это уже хорошо загнуло улыбку в виде параболы:

Тут бы успокоиться и просто порадоваться, что теперь примерно понятно откуда возникает улыбка. Но заметил проблему: IV на центре такой улыбки получался слишком большим. На картинке выше начальная вола БА = 30%, а IV на центре получилась 42-43%. В реале, насколько наблюдал, IV тоже выше чем HV, но все-таки не настолько. Если в модели снизить вероятность и размер гэпа, чтобы IV была только немного выше начальной волы, то улыбка становится почти плоской. Подсветить в чем проблема помогла HV-улыбка, на которую немного отвлекусь.
В какой-то момент захотелось проверить гипотезу, что улыбка IV показывает ожидание рынка — какая в среднем будет вола у БА, если цена придет на тот или иной страйк. Стал считать HV у каждой случайной траектории, и показывать это в виде облачка точек: по X финальная цена, куда пришла траектория на экспу, по Y — HV этой траектории. Вот что получилось для модели без гэпов:

(черные кружочки — среднее HV на соответствующем участке, решил назвать это HV-улыбкой)
Видно что IV и HV улыбки очень хорошо совпали. Но вот если добавить гэпы (и на время убрать отрицательную корреляцию между БА и волой), то картина получается такая:

Здесь уже IV и HV плохо совпадают. Но главное видно почему поднимается улыбка IV при моделировании гэпов. В самом низу проглядывает горизонтальное облачко (точки темно-серого цвета), на уровне 30% (именно такая была стартовая вола у всех траекторий). Точки из этого облачка соответствуют траекториям в которых не было гэпа. А все точки выше него (светло-серого цвета) соответствуют траекториям, в которых был хотя бы один гэп. Получается что траектории с гэпами, которые возвращались к стартовому значению цены, имеют такую же высокую волу, как и те, которые унесло далеко в сторону. Из общих соображений, решил что это неправильно. Интуитивно хочется, чтобы облако HV траекторий с гэпами, было не равномерно рассеяно, а группировалось вокруг улыбки. Что-то вроде такой картинки:

Но получил ее не совсем честным путем. А хотелось бы добавить что-то в модель, чтобы такая группировка получалась по-честному. Что-нибудь типа такого: если гэп в сторону от стартового значения цены, то идет рост волы, а если потом случается гэп в обратную сторону, то не увеличивать волу еще больше, а наоборот возвращать ее к стартовым значениям. Правда, пока не понимаю как это формализовать.
В общем, хотелось бы посоветоваться — в правильном ли направлении двигаюсь или уже занесло куда-то не туда. Допустимо ли добавлять в модель гэпы и всплески волы после них, или загиба улыбки в виде параболы можно было добиться одним VolOfVol и нужно искать ошибку в своей реализации модели Хестона?



















Какой интересный трейдинг у людей!
вы в открытом космосе )
А может вообще отказаться от улыбки и строить предполагаемое распределение будущего приращения цены по ценам опционов. И сравнивать его со своим модельным. Если модельное предположение правильно, что арбитраж между реальными ценами и модельными должен давать прибыль на достаточно долгом периоде. Причем это максимальная прибыль из всех опционных поз.
Расчет волы на данном пути может оказаться лишним, так как распределение может и не быть двупараметрическим (среднее и дисперсия).
По логике практического применения БШ всё это — попытка найти модель, оправдывающую подгонку формулы под рынок.
Хотя, возможно, на выходе может прийти какое-то новое озарение :)
Если некоторые из моделей предполагают умеренно-разумную подгонку, то здесь дело обстоит хуже.
Более-менее адекватная улыбка получалась на сериях, в которых DTE больше:
Допустим на декабрьской нефти картина такая:
И, собственно адекватность кривизны у меня сильно варьируется от волатильности ATM. Периодически бывают и линии, и другие девиации.
Мне кажется для валютных инструментов модель более интересная — появляется форвардный фактор и взаимные колебания процентных ставок.
1. Историческое распределение само по себе не дает необходимой кривизны улыбки, поскольку не учитывает кластеризацию (память) волатильности.
2. Модель Хестона в силу гауссовости приращений (как базового актива, так и волатильности) тоже не может дать достаточной кривизны улыбки.
Как с этим жить? Ну, ответ, очевиден — надо предполагать негуссовость в приращениях самого процесса и/или негауссовость в приращениях волатильности. Причем негауссовость должна быть не абы какая, а в сторону тяжелых хвостов, иначе по ЦПТ все равно будем упираться в гауссовость на старших таймфреймах.
В приниципе, то, что сделано вами с гэпами — это как раз шаг в этом направлении, но уж больно топорный и, очевидно, не соответствующий происходящему на реальном рынке.
Как сделать то же самое, но изящнее?
Я лично люблю (хотя и никому не навязываю) устойчивые процессы Леви. Правда, отсутствие дисперсии делает работу ними несколько запутанной, но там есть масштабный параметр, который эту самую дисперсию до определенной степени заменяет.
К тому же хвосты можно «подавить» (не «обрезать», а именно подавить" — см. стр 11 в первой из статей ниже), что даст конечность дисперсии с одной стороны, и проявление свойств тяжелых хвостов на не слишком больших масштабах — с другой.
Вот работа, в которой описывается мат.аппарат и даже выводится формула прайсинга для опционов:
Cartea, Howison — 2003 — Distinguished Limits of Levy-Stable Processes…
Это даст улыбку, которая, имея 4 параметра, сможет описать большинство рыночных улыбок. При этом даже безо всякой стохастической волатильности — только за счет асимметрии и скачков. Явные формулы для прайсинга — 35 и 37 на стр 26 (правда, комплексный интеграл придется посчитать).
А вот в этой работе к тому, что выше, даже прибавляется стохастическая волатильность. Правда, изящно (как у Хестона) это сделать не удалось. Поэтому формула в явном виде не получилась, так что с этой статьей я особо не разбирался, честно говоря:
Cartea, Howison -2006 — Option Pricing with Levy-Stable Processes…
Тем не менее, это направление для движения. Причем, на мой вкус, потенциально одно из самых правильных (в смысле соответствия предполагаемых моделей реальной динамике активов).
Наконец, если вам нравится генерировать и хочется напрямую убедиться, что устойчивые распределения Леви дают качественную улыбку даже при постоянной sigma, — дарю проверенный код для генерации (обычных распределений, не подавленных, так как для подавленных быстрого генератора не нашел).
Описание: sigma — масштабный параметр, аналог волатильности (хотя и не прямой).
alpha — индекс устойчивости. 0<alpha<=2. alpha = 2 соответствует гауссовскому, единственный вариант с легкими хвостами. alpha = 1 — это Коши, то есть, распределение не только без дисперсии, но и без матожидания. Т.о. для финансовых целей надо брать 1<alpha<2
beta — параметр скошенности. Не дает эффекта при alpha =2 и alpha = 1. Во всех остальных случаях «перекашивает» распределение в одну из сторон.
unirand() — вызов генератора случайного равномерно распределенного числа из интервала (0;1)
double gen_LevyStable(double alpha, double sigma, double beta)
{
//On article Rafal Weron «On Chambers-Mallows-Stuck Method...», page 8, and its latter correction by Rafal Weron for alpha=1
static double PI_TO_2=Pi/2.0;
static double V;
static double W;
static double B;
static double S;
static double tang;
if (sigma<=1e-10) return 0;
if (alpha<=1e-8) return 0;
V=Pi*(unirand()-0.5);
W=gen_expon(1.0);
if(abs(alpha-1.0)>1e-8)
{
tang=tan(Pi*alpha/2.0);
B=atan(beta*tang)/alpha;
S=pow(1+beta*beta*tang*tang, 1.0/(2.0*alpha) );
return sigma*S* sin(alpha*(V+B))/pow(cos(V),1/alpha) * pow( cos(V-alpha*(V+B))/W, (1.0-alpha)/alpha);
}
else
{
return sigma*2.0/Pi* ( (PI_TO_2+beta*V)*tan(B) — beta*log( (PI_TO_2*W*cos(V))/(PI_TO_2+beta*V) ) );
}
}
inline double inv_expon(double u, double a)
{
u=max(u, 1E-50);
u=min(u, 1-1E-50);
return(-log(1-u)/a);
}
double gen_expon(double a)
{
return inv_expon(unirand(),a);
}
P.S. Что именно не соответствует реалу — моделирование гэпов по норм.распределению (с большой сигмой) или взлет волы после гэпа? Или и то и то?
Не соответствует действительности, что есть нормально-распределенный гэп, а после него идет нормально-распределенный день. Особенно последнее.
«после него идет нормально-распределенный день» — вместо «день» имелось ввиду «вола»? Я после гэпа просто резко увеличиваю текущую волу в заданное кол-во раз, а дальше она начинает спадать с заданной скоростью к своему среднему. Т.е. после гэпа в основном играет роль уже не volofvol (который связан с норм.распред), а скорость возврата волы к среднему.
Верхний график — цена, нижний — HV (понимаю, что HV это не мгновенная вола БА, но как приблизительную оценку наверное можно считать). 8 авг случился гэп, и вола взлетела. А потом стала постепенно опадать. Так что, мне кажется, на истории можно это приблизительно измерить.
Модель представляю себе так: вот цена блуждает себе с какой-то волой, если случайно идет в зону риска (Кирилл Ильинский, 2ая лекция), то вола растет, если в обратную сторону — вола падает (но не ниже какого-то базового уровня). А потом какое-то неожиданное для рынка событие (3.03.2014, например), происходит гэп, вола подлетает, и блуждание продолжается, но уже на сильно повышенной воле. Постепенно рынок переваривает новое событие, все устаканивается, и вола начинает припадать.
Или в реале все не так?
Но кроме проблемы, как оценивать события, которые за 10 лет происходят 3-4-5 раз (какая уж тут статистика!), меня даже больше интересует вопрос — неужели все остальное время динамика волы нормальная со спадающей волатильностью?
Интуитивно для меня — вряд ли. Где-то по дороге будут случаться кризисы меньшего масштаба с меньшими подскоками волы, но все равно даже локально это будет давать более тяжелые хвосты, чем у Гаусса. Повторюсь, это моя интуиция, которая с легкостью может быть перебита результатами расчетов.
В конце концов, итоговый вопрос очень простой — есть ли у тебя на выходе из всех твоих экспериментов, тестов и измерений улыбка, в которую ты сам веришь, понимаешь, как ее настраивать под текущий рынок, и готов ли ты ее реально торговать? Идеального-то ничего нет, и если некое теоретическое построение дает рабочий инструмент, которым тебе комфортно пользоваться, и ты понимаешь, когда какую ручку крутить — ни так и отлично, пофигу мои иллюзии.
вторая картинка в посте (с улыбкой) была сгенерирована с вер-тью гэпа 1/1000. А скачок волы у меня не фиксированный задается, а как коэф-т от размера гэпа. Т.е. для маленького гэпа — будет маленький скачок волы, а для большого — большой.
Насчет спадающей волы — строил зависимости, по осиХ — приращение цены, по осиY — приращение IV (на центре). Вот, например: shot.qip.ru/00bL8k-5Dbzb2KJp/
Получается, что для приращений цены около нуля, приращения волы в основном отрицательные. Можно отсюда сделать вывод, что динамика волы имеет тенденцию к падению (когда на рынке ничего не происходит)?
Насчет толстых хвостов, пробовал так проходить по истории: беру приращение цены на некотором ТФ, беру IV на центре, перевожу ее в сигму (соотв. ТФ), делю приращение на сигму, и отслеживаю какое было максимальное значение. Получалось за квартал, бывали приращения по 20-30 сигм за раз. А у Гаусса, насколько понимаю, предел это 5-6 сигм.
Насчет итогового вопроса, если он ко мне, ответ простой — реально торговать не готов :)
И нет ли ошибки в else{} — там не проинициализированно значение B?
А вот насчет ветки, отвечающей за alpha = 1 — тут действительно косяк, скорее всего, эта ветка мне никогда не требовалась. Проверил по оригинальной статье — должно быть «tan(V)» вместо «tan(B)». Прикольно, что вы заметили, а то когда-нибудь косяк бы вылез боком.
Может дело в том, что в Паскале (пишу на Дельфи) функция Random возвращает [0, 1), а нужно чтобы было именно [0, 1]? Или это непринципиально?
P.S. Предлагаю перейти на «ты» :)
В частности, N=1млн: 0.011, N=10млн: 0.00555.
То есть, у меня все бьется. Причин может быть две. Либо у тебя где-то стоит float вместо double и просто не хватает точности, либо генератор случайных чисел плохой. Думаю, последнее.
Я использую MERSENNE TWISTER. Послал код письмом.
Получается что диапазон обрезания — тоже параметр улыбки. Чем он уже, тем она более плоская. Чем шире, тем выше ветки улыбки. Т.е. один этот параметр заменяет три параметра в моей модели: вероятность гэпа, его размер и во сколько раз подскочит вола. Это удобнее, конечно.
Интересно, что облако HV точек стало группироваться вокруг улыбки без всяких ухищрений, как и хотел. Правда, HV и IV улыбка все равно не совпадают: shot.qip.ru/00bL8k-5Dbzb2KGQ/
А правильно понимаю, что это распределение Леви нужно использовать для генерации приращений, при построении одной траектории? Или его можно использовать сразу для построения окончательного распределения цен на экспу?
И вообще — почему отдаешь предпочтение процессу Леви? Было какое-то исследование, которое показало что он лучше всего соответствует реалу? Или это просто личное имхо?
мне не очень нравится мысль с обрезанием, если честно. Если хвосты слишком тяжелые — то надо брать alpha поближе к 2, а обрезать тяжелые хвосты, если специально было взято распределение с этим свойством — это странно.
Само твое исследование показывает, что реализованная волатильность при движении к данному страйку не имеет приямого отношения к волатильности, возникающей при оценке опциона. Мне кажется, на этом тему, что они должны совпадать, есть смысл закрыть — исследование говорит само за себя.
Устойчивое распределение Леви на то и устойчивое, что обладает свойством самоподобия (именно в этом и заключается математический смысл термина «устойчивое»). Сумма N одинаково распределенных alpha-устойчивых случ. вел. имеет такое же распределение умножить на N^(1/alpha). В частности, если разделить обе части на N, то для alpha = 2 имеем стандартную ЦПТ, а для alpha = 1 — полное отсутствие сходимости (среднее N независимых величин Коши имеет такое распределение Коши).
Таким образом, при отсутствии обрезаний хвостов можно сразу генерировать распределение на экспирацию с учетом указанного масштабирующего множителя. Как только начинаются обрезания — магия пропадает :)
Именно в силу описанных свойств мне устойчивые распределения Леви и нравятся, поскольку реальный рынок в первом приближении можно считать самоподобным на разных масштабах.
В завершение отмечу, что просто «процессы Леви» — это чрезвычайно широкий класс процессов, куда входит практически все, что можно себе вообразить, если оно имеет независимые приращения. Поэтому важно говорить именно про устойчивые процессы Леви — очень узкое подмножество процессов со свойством самоподобия приращений. И если хочется сократить фразу, то лучше выкинуть слово «Леви», а не «устойчивые».
Не подскажешь — как можно численно сравнить два распределения? С целью подобрать модельное наиболее близким к рыночному? Можно ли для этой цели использовать моменты случайной величины? Если да, то достаточно ли будет первых 4х моментов?
Для процессов с тяжелыми хвостами метод моментов, очевидно, не годится просто по причине их отсутствия выше первого.
Жаль что с моментами нельзя. Была задумка подготовить заранее БД возможных вариантов модели, где каждому набору параметров модели соответствует набор первых 4х (или больше) моментов соответствующего распределения. Потом считать моменты у текущего рыночного распределения и быстро по базе находить такие наборы параметров модели с похожими моментами (первый и второй момент не учитывать). Это было бы гораздо быстрее, чем каждый раз считать интегралы.
А моменты отсутствуют именно у устойчивых процессов Леви? У рыночного распределения то эти моменты по-моему присутствуют. Считал на тиковой истории улыбки, переводил на каждом тике улыбку в распределение, считал у него первые четыре момента, и выводил их графики. График вторых моментов, например, если специально нормировать (перевести в годовую волу), то становится очень похожим на график IV (на центре).
Даже что такое характеристическая функция распределения не понимаю. Не говоря уж об комплексном интеграле.
Наугад попробовал сделать так:
x = gen_LevyStable(...);
x = x*e^(-h*|x|); //h — лямбда
Вроде таким образом «подавил» хвосты. Во всяком случае, минимум и максимум не росли с N, и моменты (считал в лоб) не менялись. Или это я что-то не то «подавил»?
В оригинале «подавление» хвостов идет за счет выбора характеристической функции, которая похожа на оригинальную, но не совсем. Так, как ты написал, подавить хвосты тоже можно, но это уже чисто для Монте-Карло. Впрочем, если аналитически ты все равно вычислять ничего не будешь, то тоже вполне себе вариант
Попробовал вычислять моменты по формуле в статье:
Насколько понял, соответствие параметров из статьи и gen_LevyStable такое: v(ню) = Alpha, k = Sigma, (q-p) = -Beta. Стал считать по этой формуле и сравнивать с расчетами по такой:
Vk — k-ый момент, f(x) — плотность распределения
Если Alpha -> 2, то первые два момента еще более-менее совпадают, но следующие уже начинают сильно отличаться. Если Alpha -> 1, то уже и первые два момента совсем разные.
Так ведь не должно быть? Может я неправильно понял параметры из первой формулы?
Implied volatility skews and stock return skewness and kurtosis implied by stock option prices
moya.bus.miami.edu/~tsu/ejf1997.pdf
немного о другом: у Bruno Dupire в какой-то работе есть упоминание, что если dSigma/dStrike != k * dSigma/dPrice то возможен какой-то замысловатый арбитраж, чему равно k не помню, кажется или 2 или 0.5
вот в этом посте вы тоже затронули вопрос прайсинга для устойчивых распределений: smart-lab.ru/blog/189863.php#comment2795832
подскажите, а вы считаете устойчиво-распределённой саму цену или логарифм цены?
если логарифм — то вроде бы первый момент не существует (точнее существует только для b толи +1 толи -1), а если саму цену — то как обрабатываете вероятность отрицательных цен?
Наличие первого момента зависит не от параметра скоса (полагаю, именно его вы назвали b), а от индекса устойчивости alpha.
За исключением краевого случая alpha = 2, соответствующего обычному броуновскому движению, при всех остальных 0<alpha<2 существуют (то есть, конечны) все моменты порядка строго меньше alpha. У обычного броуновского движения существуют все моменты.
Что касается параметра скоса, то его краевые значения +1 и -1 при alpha<1, насколько я помню, соответствуют наличию четкой границы распределения снизу или сверху. То есть, при b=1 можно выбрать такой параметр сдвига m, что распределение будет неотрицательно (возможно, даже при m=0 — сейчас сходу не вспомню).
положим x=S(T) — цена на момент экспирации имеет какую-то плотность распределения g(x), а так же известно, что y=ln(x) имеет плотность распределения f(y), тогда поскольку премия колл опциона это матожидание выплаты, то:
возможно я ошибаюсь, но в 3й строке интеграл расходится, не?
Сейчас посмотрел уже упоминавшуюся мною в этой ветке статью Cartea, Howison 2003 — там прямым текстом сказано, что они потому и работают с Damped Levy Stable, что сами Levy Stable обладают этим пренеприятным свойством — только при b=-1 экспоненциальный момент конечен.
Как-то не заострял свое внимание на этом моменте, рад, что вы сейчас вы это вытащили в явном виде.
С точки зрения практики, это приводит к двухходовке:
1. Гауссовское распределение надо обобщать в сторону более «тяжелых» хвостов. «Тяжелых» — не в математическом смысле, а в бытовом — чтобы большие отклонения 2-3-4-5 сигма более вероятны, чем у Гаусса. При этом желательно быть «близким» к масштабной инвариантности, поскольку она в первом приближении есть в реальных рядах. Идеально инвариантны и с строго математически тяжелыми хвостами — устойчивые процессы.
2.Поскольку чистый устойчивый Леви имеет обсуждаемую сложность с бесконечностью экспоненциальных моментов, и, как следствие, с бесконечностью цены опциона колл, то приходится тем или иной степени подавлять хвосты. Можно обрезать — но это грубо, топорно и не соответствует реальной жизни. Поэтому надо как-то подавлять. Ну, вот например, как в упомянутой статье — через дополнительное экспоненциальное подавление меры W в триплете Леви.
Это позволяет и получить все моменты конечными, и вывести длинную, но все же явную формулу для прайсинга опционов.
Кстати, если возвращаться к самоподобию (фрактальности), то оно в реальных рядах имеется тоже в первом, грубом приближении. В реальности же экспонента Херста по мере роста масштаба прибилижается сверху к 1/2. Подавленные процессы как раз-таки воспроизводят естественным образом этот эффект по причине конечности моментов и как следствие доминирование эфекта ЦПТ на сверхбольших масштабах.
если рассмотреть модель где y = ln(x) распределена как f(y) = w1 * phi(mu1, s1^2) + w2 * phi(mu2, s2^2),
то есть логарифм цены распределён как взвешенная сумма двух гауссиан (что важно — с ненулевыми mu), то такой простой и тривиальноинтегрируемой моделью можно сделать аж первых пять моментов распределения практически любыми (в том числе например загнать 4й момент поближе к бесконечности — это как раз тяжёлые хвосты)
в итоге это интегрируется во взвесь двух обычных блэков-шоулзов + ненулевые mu добавят некоторый гарнир
очевидно w1 + w2 = 1 => mu1 и mu2 не могут быть одного знака, поэтому вклад от phi(mu1, s1^2) можно в некотором смысле интерпретировать как точку зрения оптимистов, phi(mu2, s2^2) — соответственно пессимистов, а w1 и w2 — как меру их проявленности
дальше можно пофилосовствовать о том, что мы знаем всё необходимое для того, чтобы выполнить применение критерия келли «наоборот», и понять, что одна из сторон систематически не на оптимальном f, но это уже совсем другая история…
Возвращаясь к лог-устойчивым распределениям — наиболее выпукло парадокс проявляется на валютах, получается что call на, например, eur/usd стоит бесконечно, а put на usd/eur (что вроде бы то же самое) имеет конечную цену
Выходит что:
— или сами по себе колы причина парадокса (да и фьючи тоже)
— или устойчиво распределён не y=ln(x), а что-то вроде y=x^(1/g)-c, где g>=1, но меньше alpha
— или это «санкт-петербургский парадокс», когда стоимость игры с бесконечным матожиданием конечна и даже не очень дорога
Когда все моменты конечны — распределение можно воспроизвести смесью гауссов, если уж не двух, то трёх должно хватать в большинстве случаев.
PS: а вы получается и дельту по облегчённому распределению считаете? )))
А по Вашим выкладкам получается, что два пика не являются неэффективностью, а вполне допустимая ситуация, когда рынок явно разделяется на два лагеря: один закладывается на тренд вниз, а другой — вверх?
> периодически замечаю, что у рыночного распределения
> имеются два пика (пример)
Вы плотность через ABCDES-кривую волатильности считаете?
Если да, то когда я туда последний раз смотрел (в 2012) не помню чтобы настолько хорошо выделялось 2 пика. Интересный вопрос, не готов ответить ...
Попадает ли в тихое время (например, с 11:00 до 13:00 MSK) провал в плотности на страйк (имеется ввиду цена кратная 5000)?
Что происходит с провалом, если фьюч проходит через страйк?
Если провал:
— обычно между страйками
— существенно изменяется при проходе фьюча через страйк
— на ближайших страйках биды/офера выше/ниже теорцены биржи
то это скорее всего особенность способа подгонки параметров кривой со стороны биржи, задуматься стоит если провал устойчив и теорцены попадают в рыночный спред
Плотность из цен опционов можно извлекать не только второй производной, но и как ни странно интегрированием.
Процесс очень похож на расчёт викса и совершенно model free, т.е. не предполагает ровным счётом ничего кроме «цена = ожидание выплаты».
Любой момент распределения можно вычислить, просуммировав (проинтегрировав) с некоторыми коэффициентами премии OTM опционов
Для второго момента (волатильности) получится формула викса moex.com/ru/index/RVI/info/
Для i-го — будет добавляться что-то типа (K-S(T0))^(i-2) в числителе, наверное ещё что-то вылезет, могу ошибаться.
А почему оно так получается можно прочитать у Emmanuel Derman
Таким образом, например, по пяти моментам можно вычислить подходящую смесь двух гауссов.
Далее по полученному распределению — посчитать цены, и измерить насколько они вне бид/аск спредов, назвать это штрафной функцией и минимизировать штраф изменяя {w, mu, s^2}
После этого у меня таких явных двух пиков не выходит (у «моих» пессимистов сигма существенно больше)
> Мне казалось, что это неэффективность, но смущало что
> она иногда долго держится (бывает по нескольку дней).
> А по Вашим выкладкам получается, что два пика не являются
> неэффективностью, а вполне допустимая ситуация, когда рынок
> явно разделяется на два лагеря: один закладывается на тренд
> вниз, а другой — вверх?
Я подозреваю всё же, что это спецэффекты при конвертации биржевой кривой в плотность через вторую производную, попробуйте сделать интегрирование и восстановить плотность через моменты.
Два выраженных пика — не типично, но допустимо. Обычно смесь не имеет точек перегиба.
Процесс соответствующий смеси гауссов сам по себе вроде бы не создаёт арбитража:
dPrice = Price * (uniform_random() < w1? normal_random(mu1, s1^2): normal_random(mu2, s2^2));
PS: обращу ещё внимание, что даже с сильным увеличением T форма распределения не размыливается по цпт до нормального, но эмпирически, как заметил Андрей, должно бы
На RTS сейчас этого нет, но есть на Si. Вот пара скриншотов: на первом видно агрессивный бид, который изогнул улыбку. А на втором видно как из-за этого появилось два пика у распределения.
Т.е. каждый раз, когда возникают два пика, вижу что это не из-за каких-то глюков биржевой улыбки, а объективно из-за какого-то бида. Вот только не понимаю почему рынок это сразу не исправляет. По идее, можно было бы продавать повышенный страйк, откупать оба соседних, и ждать исправления улыбки. По моим виртуальным замерам, если покупать бабочку на этом страйке в момент такого изгиба, то потом восстановление улыбки может приносить около +10% от задействованного ГО. Если бы все это делали, то как раз постепенно это выровняло бы улыбку и два пика исчезли бы. Но почему-то такая ситуация бывает продолжается несколько дней. То ли потому что те кто это видят — затарены уже под завязку. То ли тут есть какие-то подводные камни и вообще теоретически это допустимая ситуация, без всяких арбитражных возможностей.
P.S. Спасибо за другой способ вычисления распределения по ценам. Мало что понял (туго с математикой), но буду перечитывать. Правильно ли понял, что можно по первым заданным моментам построить целое распределение?
> Вот только не понимаю почему рынок это сразу
> не исправляет. По идее, можно было бы продавать
> повышенный страйк, откупать оба соседних, и
> ждать исправления улыбки.
Вы всё правильно написали, такой сильный провал в плотности может быть хорошим поводом для открытия бабочки. Обратите внимание, что:
1) на соседних страйках нет оферов
2) из-за того, что рядом широкий спред — кривую, не ухудшив штрафную метрику, можно провести и например вот так: s7.hostingkartinok.com/uploads/images/2014/11/2a25c183e4b541764478591addaa1b6c.png
Возможно ABCDES кривую именно вот так как я нарисовал и нельзя провести. Погуглите другие параметризации, неплохая альтернатива — параметризовать кривую через ATM, RR и BF (об этом доступно писал Олег Мубаракшин, в википедии как-то слишком не понятно)
> Правильно ли понял, что можно по первым заданным
> моментам построить целое распределение?
Не совсем, теоретически множество различных распределений имеющих k первых моментов равных заданным — бесконечно. Но при некоторых дополнительных предположениях, о которых написано ниже — круг кандидатов сильно сужается
Например у вас дано 5 моментов, вы можете воспроизвести эти моменты смесью двух нормальных, а можете смесью двух равномерных (про равномерные стоит перепроверить, сам удивлён). Первые пять моментов и так и так будут одинаковые, но что-то со вторым вариантом явно не так.
Дело вот в чём, если рассматривать процесс с режимами, то есть когда изменение цены с вероятностью w_i имеет распределение distribution_i(mu_i, s_i^2) — какие-то абстрактные распределения (не обязательно нормальные) с конечными средними и дисперсиями, то по ЦПТ всё равно получится, что величина sum(dPrice) имеет плотность sum(w_i * normal(mu_i, s_i^2))
Поэтому для процесса с режимами, где режимов конечное число и у распределений внутри режима конечны первые два момента, правомерно игнорировать глубинные структуры и искать плотность суммы как смесь n гауссов.
PS: чтобы не вводить вас в заблуждение — то, что мы сейчас обсуждаем это не то же самое что то как я зарабатываю на опционах, это теория, которой я пытаюсь компактно объяснить свои стратегии найденные численными методами
То что нет оферов — это просто их сняли на выходные. Сейчас картинка такая. Или даже вот такой скрин — тут лучше видно, что приходится изгибать улыбку ступенькой, чтобы пройти между бид-асками. (толстая линия — биржевая улыбка, тонкая — самостоятельная подгонка).
Был на 7ой конфе, слушал выступление Олега про метод Vanna-Volga. Очень интересная модель с 3мя параметрами, каждый из которых имеет физ.смысл — это конечно гораздо лучше чем ABCDES. Но к моему большому сожалению — там недоступный мне уровень математики. Посчитать интеграл или взять вторую производную еще как-то могу, а вот решить систему диф.уравнений — уже никак :(
Насчет смеси n-гауссов — интересно. У меня была похожая идея, моделировать три режима волы: пониженная (тухляк), обычная, повышенная (эквивалент гэпам). Но чтоб каждому режиму еще и свой тренд задавать — не додумался. А Вы реально такую модель построили, приближаете ею рыночную улыбку и используете в торговле?
В торговле использую модель OptPrice = (BSMix + Error(z)) * (1 + Correction(z))
BSMix — цена смеси двух или трёх гауссов, Correction(z) — жёсткая коррекция, чтобы Error(z) имел нулевое среднее.
Correction(z) колибруется по истории и задаётся однажды и надолго.
Чтобы весь цимес не сосредоточился в Correction — нужно дополнительное условие, например, что abs(Correction(z)) <= 0.05 и/или, что какая-то производная Correction(z) ограничена.
z — это какая-нибудь не особо сложная мера удалённости страйка, от ATM, например дельта.
Дальше уже детали, которые я не могу обсуждать не в ущерб себе.
Но с удовольствием обсужу в обмен на вот такую задачу:
Известно, что акция выплатит дивиденды d, а дата отсечки — T_d, на дату T > T_d торгуются американские опционы (будем считать, что по справедливым ценам).
Сколько должны стоить опционы (можно даже американские маржируемые) на фьючерс на эту акцию с датой экспирации тоже T?
хочется что-то типа FutOptPrice = StockOptPrice + F(d, T_d, T, S, K)
Насчет задачки, честно говоря, у меня очень ограниченные познания в опционной науке. Поскольку у нас опционы пока тока на фьючи, то опционами на акции еще не интересовался. Тут лучше у спецов спросить.
Смесь — это когда с вероятностью p реализуется одно распределение, а с вероятностью (1-p) — другое. То, что что вы пишете дальше, подсказывает, что вы это понимаете, просто обозначили неправильно, но на всякий случай обратите внимание (к тому же вдруг еще кто-то прочтет).
Что касается дальнейших рассуждений, то в первую очередь сама концепция оптимиста и пессимиста является спорной. К тому же, отдельный вопрос — а эти ваши оптимист и пессимист — они финансовую математику знают? В том смысле, что они прайсят по-тупому (через физическое распределение — то есть, через то, которое они предполагают) или по-умному (по риск-нейтральному распределению). Во втором случае параметры mu1 и mu2 у вас исчезнут, заменившись на безрисковую ставку.
Но в целом сами ваши наблюдения за «парадоксами» заставляют задуматься над этим бинарным оптимистично-пессимистичным разложением (или не бинарным, а на большее число — не столь важно).
Что касается вопроса в «PS», то, на мой взгляд, все греки надо считать по той модели, по которой торгуешь. Так что да, считаю по модели не только дельту, но и тэту с вегой.
> anon, то, что вы пишете в начале выглядит не как смесь,
> а как взвешенная сумма.
> Но сумма нормальных — нормальная и никак не получится
> в ней подобрать произвольные моменты.
да, я как раз беспокоился, чтобы оно будет выглядеть как взвешенная сумма случайных величин, а не распределений ...
> Смесь — это когда с вероятностью p реализуется одно
> распределение, а с вероятностью (1-p) — другое.
да, имелось ввиду именно вот это.
> Что касается дальнейших рассуждений, то в первую очередь
> сама концепция оптимиста и пессимиста является спорной.
> К тому же, отдельный вопрос — а эти ваши оптимист и
> пессимист — они финансовую математику знают? В том смысле,
> что они прайсят по-тупому (через физическое распределение
> — то есть, через то, которое они предполагают) или
> по-умному (по риск-нейтральному распределению). Во
> втором случае параметры mu1 и mu2 у вас исчезнут,
> заменившись на безрисковую ставку.
Вот например на транснефти ставка репо около 6%, а во фьючерсе SiH5 порядка 10%, а на совсем неликвидах и вовсе отрицательная. Какая же тогда ставка riskfree? Я бы сказал, что для оптимиста и пессимиста безрисковые ставки как раз и есть mu1 и mu2, то есть одни зарабатывают на размещении, другие на привлечении.
Вобще про оптимистов/пессимистов — это «сопроводительный текст», основной поинт всё же в том, что двумя гауссами можно воспроизвести довольно много моментов
А теперь, как говорится, внимание, вопрос! А дальше-то что? Ну, вот получили какие-то 5, или 7, или 9 параметров. Дальше что с ними делать? Они должны быть стационарными во времени? Или нет? Если да, то почему, и как их оценить тогда по динамике базового актива, а не по текущей улыбке.
Если нет (нестационарные) — то что пользы в принципе в том, что мы их нашли для улыбки в текущий момент времени? Может, хотя бы какие-то устойчивые тенденции у них есть? Например, как то, что абсцисса «дна» улыбки движется к точке денег по мере экспирации. Но выявление и количественное описание (!) таких закономерностей — очень трудоемкая задача.
Поэтому прежде чем начинать раскладывать подразумеваемое распределение на сумму/смесь/произведение каких-то компонент, крайне полезно спросить себя — а что я вообще-то ожидаю от такой модели? Я понимаю, какие закономерности будут у ее параметров с течением времени? Или зачем тогда я вообще беру подобное представление?
Ответы на эти вопросы по сути дают дорожную карту, как использовать полученные результаты в своей торговле. Если их нет — то выход на практическую полезность представляется мне крайне сомнительным.
Была такая идея — может удастся построить модель распределения, которое будет «средним» для рыночного (подразумеваемого рыночной улыбкой). Просто стал нормировать рыночное на время, цену и IV ATM, и смотреть на него в динамике. Мне показалось, что можно попытаться найти некое среднее для него. Посмотрел моменты (M3 и M4) на истории, они скачут конечно, но ощущение что вокруг некоторого медленно меняющегося среднего. Если брать такие средние на данный момент M3/M4, и сделать модель для поведения M2 (~IV ATM, моделировать как в Хестоне, иногда подкалибровывать к рынку), то вот и готовое «среднее» распределение. И относительно него уже арбитражить рыночную улыбку.
Как такая идея? Или можешь сразу забраковать?
www.facebook.com/groups/549020375200057/
Эта группа посвящена обсуждению лекций Кирилла Ильинского, но завтра (в среду, 29 октября) будет дискуссия на очень близкую к вашему посту тему:
Докладчики и темы:
Vladimir Tvardovsky Использование моделей стохастической волатильности на опционном рынке (на примере моделей Хестона и Калинина-Ильинского)
Sergei Vasilev Multi-dvega
(Что такое dvega, понятия не имею, так что имею в виду прежде всего доклад Твардовского)
Большая часть будет участовать онлайн через AdobeConnect, физически на месте будет всего 7 человек. Так что вступайте в группу, напишите о желании участвовать и получите код доступа для дистанционного участия.
Если нужно, я могу отправить вам приглашение в группу — для этого мне нужен ваш e-mail, на который заристрирован ваш аккаунт в FB
P.S. Сцуко, я оказывается, не могу даже персональные сообщения отправлять из-за низкого рейтинга. Блин, вот я смарт-лабовский нищеброд… Ладно, пусть все читают это сообщение
Насчет рейтинга — явная несправедливость. Плюсанул и в профиль (уже давно) и комменты, сделал что мог.
Тимофей, может есть возможность подкрутить рейтинг Андрею? Все таки, один из самых продвинутых опционщиков на Смарт-лабе :)
Параметры соответствуют формуле в моем посте
volav = x[0]; ( средняя волатильность )
volvol = x[1] ;
k = x[2] ;
ro = x[3];
и такие наборы x получались
{0.3063,0.6891,0.3383,-0.4830}
{0.2491,0.4997,0.2781,-0.6849}
{0.2629,0.5174,0.2641,-0.6468}
время — 30 — 40 суток до экспирации
Не подскажете — а как генерировали приращения dZ и dW, чтобы корреляция между ними была равна заданной величине?
А формула ниже
ro[j] * dw1 + Math.Sqrt( 1.0 — ro[j] * ro[j] ) * dw2
Генерация простых нормальных чисел, сам рандомайзер имхо не так принципиален. Ошибки не из-за него возникают
?
(dZ/dW из Вашего поста, пункт а)
Пример1 (корреляция=-0.52)
Пример2 (корреляция=-0.91)
Пример3 (корреляция=+0.35)
Это нормально и допустимо, или у всех пар корреляция должна быть -0.5?
Присматриваюсь к модели jump diffusion, читаю Jump Diffusion Models for Option Pricing vs. the Black Scholes Model.pdf
таймфрейм — минутки. В основном экспериментировал с длиной 830 точек (эквивалент одной торговой сессии). Но пробовал и большее кол-во точек (эквивалент месяцу и кварталу). Все равно линия получалась. Ночь и выходные не учитывал (т.е. как-будто торговля идет круглосуточно).
Такой маленький таймфрейм мог быть причиной, почему не получилась парабола в улыбке?
ну, и вопрос до кучи:
а нафи… т.е. зачем те модели? )))
имхо, ужо пора в скайпе потрындеть и на эту тему тоже )))
Красивые облака, сочные краски :)
Но они ведь говорят о том какая была корреляция между БА и IV ATM в тот или иной период времени? А мне хотелось проверить как соотносятся HV траекторий, которые на экспу пришли на некий страйк, со справедливой IV которая была на этом страйке.
Насчет «а нафига?» — просто хочется и интересно. Может чего-то полезного с практической точки зрения удастся накопать.