SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. vlad1024
Статистические модели трендов. Смещение среднего. (Дополненное)
- 02 марта 2012, 13:45
- |
Попросили объяснить что такое персистентность без специальных терминов и как она связана с трендовостью рынка. Совсем, без терминов вряд ли получится, но если их минимизировать, достаточно понятия — плотности вероятности.
Что такое плотность вероятности? Это функция интеграл интервала которой, дает нам вероятность попадания в этот интервал. Или в простейшем случаи, если мы рассматриваем ее эмпирическую оценку в виде гистограммы распределения это будет просто частота попадания в набор фиксированных интервалов.
Для примера рассмотрим гистограмму нормального распределения.
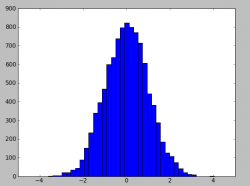
Собственно что мы видим — разбиение на набор фиксированных интервалов, затем подсчет попадания каждого значения в тот или иной интервал, который дает частоту. Если мы хотим посчитать частоту попадания в бОльший интервал например от 0 до 2, то нам необходимо сложить(проинтегрировать) частоту попадания во все маленькие интервалы внутри этого отрезка [0, 2]. Таким образом плотность вероятности дает возможность, зная интервал, получить вероятность попадания в него. Или если рассматривать на более «интуитивном» уровне — показывает какие значения выпадают более часто, а какие менее. В приведенном примере, наиболее часто выпадают значения вокруг нуля распределения и затем оно постепенно спадает.
Если мы рассмотрим, распределение как набор значений расположенных во времени (привычные для трейдинга представления в виде графиков числовых рядов). То получим для все того же нормального(гауссового) распределения следующую картинку:
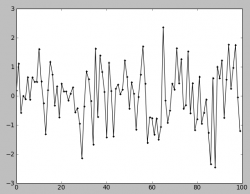
Как и ожидалось из гистограммы распределения, 95% значений находятся внутри интервала от -2 до +2, с центром в нуле.
Каждый наверняка видел график случайного блуждания и этот на него мало похож. Разница в том, что для того чтобы получить случайное блуждание необходимо последовательно сложить эти значения. Или наоборот чтобы получить из случайного блуждания — распределение приращений, необходимо взять разность соседних значений.
Таким образом мы подходим к первой простейшей модели тренда. Рассмотрим распределение приращений:
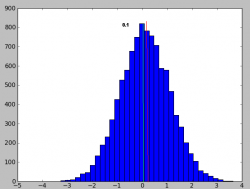
которое практически на глаз не отличается от предыдущего, но среднее (центр) сдвинуто на +0.1. Теперь просуммируем значения распределений для первого случая с нулевым и положительным (+0.1) смещением среднего, таким образом получим два графика случайных блужданий.
Первый, без смещения в мат ожидании приращений:
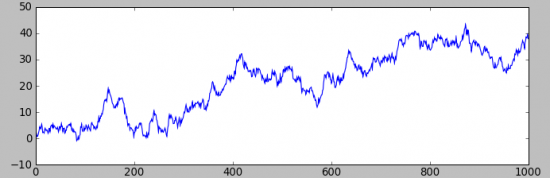
А второй, с «ничтожным» (ели разлечимым на графике распределения приращений) смещением(+0.1):
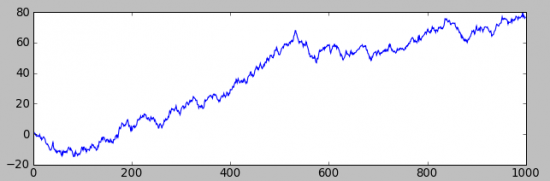
Разница, разительная, но на первом графике — заработать не возможно, а на втором вполне.
В данном случае мы рассматриваем, зависимость(смещение в мат. ожидании), которая не изменяется во времени, то есть стационарна, 0 для всего графика, или +0.1 другого. Теперь представим что эти значения сами изменяются во времени, и представляют к примеру кусочно-постоянную функцию. То есть набор констант, из которого мы выбираем значение, действующее на каком-то интервале. Соответственно если это значение положительное возникает «растущий кусок тренда», если отрицательное — «падающий». А сам график «сшит» из таких интервалов с постоянными значениями. Таким образом мы получим приближенную к реальности простейшую динамическую модель тренда. У которое стационарное среднее приращений равняется 0, но при этом существуют интервалы на которых оно отклоняется от 0 как в положительную так и отрицательную сторону. При этом в среднем количество таких участков «уравновешивается» и мы получаем среднее всех приращений близким к нулю.
Или если мы будем рассматривать среднее, как функцию времени, то для кусочно-постоянной модели, получим следующую картинку:
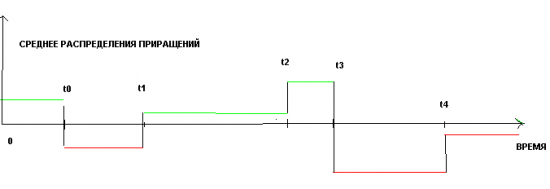
Или ввиде формулы, P_i+1 = P_i + A_k + N(0, 1) , где A_k это значение среднего на данном временном интервале(t_k, t_k+1), N(0, 1) стандартизированное нормальное распределение, а Pi это получившийся стохастический процесс.
Для примера рассмотрим реализацию такого стохастического процесса, при t_k = (0, 100, 200, 400, 450, 600, 650) и A_k = (+0.1, -0.1, +0.05, +0.15, -0.2, -0.05), что примерно соответствует представленному выше графику зависимости от времени.
Первая реализация:
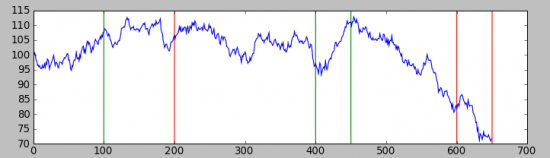
Вторая реализация:
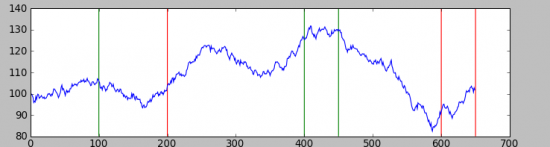
Как видно они мало похожи, и в них гораздо менее очевидно наличие трендов чем в простейшем стационарном случаи, но тем не менее они там присутствуют, а значит на таком процессе возможно заработать.
В следующей серии, мы поговорим о еще одной модели тренда, которая связана с персистентностью, или более конкретно, мы будем понимать под персистентностью — авто-регрессивность числового ряда.
Что такое плотность вероятности? Это функция интеграл интервала которой, дает нам вероятность попадания в этот интервал. Или в простейшем случаи, если мы рассматриваем ее эмпирическую оценку в виде гистограммы распределения это будет просто частота попадания в набор фиксированных интервалов.
Для примера рассмотрим гистограмму нормального распределения.

Собственно что мы видим — разбиение на набор фиксированных интервалов, затем подсчет попадания каждого значения в тот или иной интервал, который дает частоту. Если мы хотим посчитать частоту попадания в бОльший интервал например от 0 до 2, то нам необходимо сложить(проинтегрировать) частоту попадания во все маленькие интервалы внутри этого отрезка [0, 2]. Таким образом плотность вероятности дает возможность, зная интервал, получить вероятность попадания в него. Или если рассматривать на более «интуитивном» уровне — показывает какие значения выпадают более часто, а какие менее. В приведенном примере, наиболее часто выпадают значения вокруг нуля распределения и затем оно постепенно спадает.
Если мы рассмотрим, распределение как набор значений расположенных во времени (привычные для трейдинга представления в виде графиков числовых рядов). То получим для все того же нормального(гауссового) распределения следующую картинку:

Как и ожидалось из гистограммы распределения, 95% значений находятся внутри интервала от -2 до +2, с центром в нуле.
Каждый наверняка видел график случайного блуждания и этот на него мало похож. Разница в том, что для того чтобы получить случайное блуждание необходимо последовательно сложить эти значения. Или наоборот чтобы получить из случайного блуждания — распределение приращений, необходимо взять разность соседних значений.
Таким образом мы подходим к первой простейшей модели тренда. Рассмотрим распределение приращений:

которое практически на глаз не отличается от предыдущего, но среднее (центр) сдвинуто на +0.1. Теперь просуммируем значения распределений для первого случая с нулевым и положительным (+0.1) смещением среднего, таким образом получим два графика случайных блужданий.
Первый, без смещения в мат ожидании приращений:

А второй, с «ничтожным» (ели разлечимым на графике распределения приращений) смещением(+0.1):

Разница, разительная, но на первом графике — заработать не возможно, а на втором вполне.
В данном случае мы рассматриваем, зависимость(смещение в мат. ожидании), которая не изменяется во времени, то есть стационарна, 0 для всего графика, или +0.1 другого. Теперь представим что эти значения сами изменяются во времени, и представляют к примеру кусочно-постоянную функцию. То есть набор констант, из которого мы выбираем значение, действующее на каком-то интервале. Соответственно если это значение положительное возникает «растущий кусок тренда», если отрицательное — «падающий». А сам график «сшит» из таких интервалов с постоянными значениями. Таким образом мы получим приближенную к реальности простейшую динамическую модель тренда. У которое стационарное среднее приращений равняется 0, но при этом существуют интервалы на которых оно отклоняется от 0 как в положительную так и отрицательную сторону. При этом в среднем количество таких участков «уравновешивается» и мы получаем среднее всех приращений близким к нулю.
Или если мы будем рассматривать среднее, как функцию времени, то для кусочно-постоянной модели, получим следующую картинку:

Или ввиде формулы, P_i+1 = P_i + A_k + N(0, 1) , где A_k это значение среднего на данном временном интервале(t_k, t_k+1), N(0, 1) стандартизированное нормальное распределение, а Pi это получившийся стохастический процесс.
Для примера рассмотрим реализацию такого стохастического процесса, при t_k = (0, 100, 200, 400, 450, 600, 650) и A_k = (+0.1, -0.1, +0.05, +0.15, -0.2, -0.05), что примерно соответствует представленному выше графику зависимости от времени.
Первая реализация:

Вторая реализация:

Как видно они мало похожи, и в них гораздо менее очевидно наличие трендов чем в простейшем стационарном случаи, но тем не менее они там присутствуют, а значит на таком процессе возможно заработать.
В следующей серии, мы поговорим о еще одной модели тренда, которая связана с персистентностью, или более конкретно, мы будем понимать под персистентностью — авто-регрессивность числового ряда.
теги блога vlad1024
- algotrading
- AMD
- books
- brexit
- future
- hft
- machine learning
- markets
- mercedes
- perfect world
- python
- research
- smart lab
- statistic
- stocksharp
- акции
- амд
- беспилотники
- бизнес
- биржа
- биткойн
- ВВП
- веселье
- викторина
- вопрос
- геополитика
- Глазьев
- госдума
- данные
- долгосрочные инвестиции
- доллар
- доллар рубль
- закон Яровой
- запад
- ИИ
- инвестиции
- инвестиция
- индекс оптимизма
- интернет
- инфляция
- капитализм
- коинтеграция
- коррекция
- кризис
- Кудрин
- кукловод
- ликбез
- ЛЧИ 2011
- ЛЧИ 2011
- макроэкономика
- маразм крепчал
- модель тренда
- недвижка
- нефть
- новая экономика
- опрос
- оффтоп
- патриотизм
- политика
- популяция
- прохоров
- пузыри
- регулирование
- роскомнадзор
- рубль
- рынок
- системы
- спекулянты
- спекуляции
- статистика
- ТА
- такси
- теория вероятности
- теория Доу
- технический анализ
- торговля
- торговые сигналы
- трамп
- трейдинг
- философия
- форекс
- фундамент
- Хованская
- Хронология
- ЦБ
- электромобиль
- эффективность
- эффективный рынок
- юмор
- я у мамы аналлитик
- яндекс
- яровая



















Временной ряд на финансовом рынке — не Винеровский процесс.
Может тогда возьмете на себя труд объяснить популярно публике, что есть Винеровский процессс… А вдруг кто-то заинтересуется как премии по Black-Sholes считают )
Гауссовость тут или какое-то другое распределение приращений — не важно, главное в этой модели тренда, что происходит динамическое смещение центра(мат.ожидания/медианы) распределения приращений от нуля. Собственно чем занимается уважаемый А. Г. и зарабатывает деньги на рынке, это исследование оптимальных оценок в рамках данных моделей, более подробно можно почитать у него на сайте.
автору +
То что гаусс не работает оно и понятно — на нем на дистанции и заработать нельзя.
Просто лень было все в одном посте писать, но решил начать с азов. )
собственно пример торговли по Горчакову в чистом виде :)
В том то и дело, что либо случайность и теорвер (это неотделимо), либо цены предсказуемы точно по прошлым значениям (просто мы не знаем этого «закона»).
А из теорвера все потенциально просто:- надо искать статзависимость прошлого и будущих приращений цен.
Только одна «незадача» — классический теорвер из вузовских учебников — это теория независимых случайных величин и их модификаций на разного рода процессы (мартингал — это как одна из модификаций независимости).
А мы решаем задачу «перпендикулярную» тому, чему учат в теорвере и тому, что активно развивалось. А зависимые выборки, не сводящиеся к независимому случаю при переходе от непрерывного времени к дискретному, — это «падчерица» фундаментального теорвера, так как общую и красивую теорию на них не построишь и докторскую не защитишь.
есть массив данных цены
1,2,3,4,5,4,4,3,2...., n
начинаем считать приращение с 1по n. Не нашли.
с 2 по n
с 3… с 4, с 5, с4, с4 по n.
правда толку не будет наверное, потому что как никак это история… свершившийся факт.
а вот для интересу можно, только вычислительные мощности нужны намного более серьезные, чем наши ПК :)
я кончено могу ошибаться. это лишь мое имхо после прочтения хорошего поста)
Если рассматривать значения смещения среднего и дисперсии, как процессы с «тяжелыми хвостами», одномерное распределение приведенного процесса тоже будет иметь «тяжелые хвосты».
Де-факто я ответил на Ваш вопрос выше
smart-lab.ru/blog/43277.php#comment720985
В том то и дело, глобальное среднее у такого процесса может быть нулевым, а на отрезках с одним и тем же сдвигом среднее произведений двух соседних приращений положительно (так как глобальное среднее нуль, то мы не вычитаем произведение средних)
Ниже правильно vlad1024 сказал, что хвосты порождает неоднородность среднего и дисперсии. Мы имеем не нормальное распределение N(0,s), а распределение N(a,b*s), где а и b в свою очередь случайные величины и закон такого распределения при абсолютно непрерывных распределениях a и b уже будет интегралом от нормальной плотности n(a,b*s), умноженной на плотности a и b. А у этого интеграла при разных распределениях a и b могут быть «хвосты» любой тяжести.
Вообще эта модель интересна тем, что в ее рамках можно объяснить любую одномерную статистику от приращений цен. Но в этом и ее слабость — она ничего не объясняет, а лишь дает пути поиска статпреимущества.