SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. KiboR
Саймон Вайн. Mission completed.
- 26 июля 2020, 13:27
- |
Ставил себе цель 18.02.2020 перелопатить книгу Саймона Вайна «Опционы. Полный курс для профессионалов» от корки до корки, сегодня 26.07.2020 миссия завершена, загрузка книги в кору головного мозга прошла на 100%.
На изучение материала ушло чуть больше 5 месяцев. Книга, нужно признать, очень зачётная. Материал переваривал долго и тщательно, поэтому столько времени заняло. Читал обычно по выходным, на буднях некогда просто.
Как говорит Наталья Грэйс в своих ютубошных роликах: «Можно прочитав книгу за 50 рублей потом на ней кормиться всю жизнь. Людям лень читать, им проще заплатить 50 000 руб за ваш семинар и попросить разжевать материал, чем самим читать книгу за 50 рублей».
Справедливости ради нужно отметить, что книга Саймона Вайна стоила порядка 1200 руб, семинары по опционам я проводить не собираюсь (хотя уже начинают приглашать), целью прочтения книги я ставил желание поближе познакомиться с опционами и научиться на них зарабатывать. Обучать людей нет никакого желания, ни возможности, нужно двигаться дальше самому.
Ставлю новую цель — добить до конца этого года книгу Шелдона Натенберга.
Когда ты ставишь цель и достигаешь потом ее — наступает невероятное чувство эстетического удовольствия. Ты говоришь сам себе: «да, я смог, не сломался в пути и не свернул с этой цели». Это очень круто.
Завершить свои топики по книге Саймона Вайна я хотел бы приложением «моделирование», где даются формулы для расчёта опционов.
Тру-опционщик должен знать всего лишь 3 формулы, с помощью которых он потом сможет крутить весь мир вокруг своей оси.
Формула №1: Цена опциона колл на бездивидендную акцию по модели МБШ
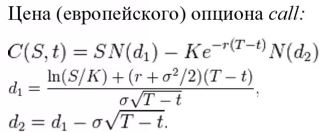
Формула №2: паритет между ценой опциона колл и пут
С + K*e^(-r*(T-t)) = P + S
Из формулы №1 и формулы №2 получаем формулу №3: Цена опциона пут на бездивидендную акцию по модели МБШ
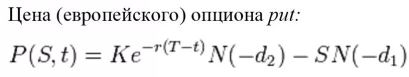
N (d1) и N (d2) — это функция нормального распределения от числа, встроена в Excel, нужно набрать «нормрасп» с параметрами (d1;0;1;1), где d1 — это то самое число, функцию нормального распределения от которого мы считаем, 0 — мат.ожидание, 1 — стандартное отклонение, 1 — признак интегрального исчисления, который нам даёт вероятность:
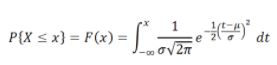
Необходимо также запомнить, что N(d2) в МБШ — это вероятность того, что опцион с конкретным выбранным страйком будет исполнен.
Если будет время, напишу как-нибудь статью на Яндекс-Дзене как выводится МБШ. Если разобраться какой смысл придается каждому элементу из формулы, то МБШ заиграет новыми красками и расчёты начнут приносить удовольствие.
Любите опционы.
С уважением, Карлсон.
---
p.s. кому интересно, свои мысли по рынку кидаю в канал «Фондовый рынок глазами Карлсона» (t.me/KarLsoH), там же есть и опционный чат.
На изучение материала ушло чуть больше 5 месяцев. Книга, нужно признать, очень зачётная. Материал переваривал долго и тщательно, поэтому столько времени заняло. Читал обычно по выходным, на буднях некогда просто.
Как говорит Наталья Грэйс в своих ютубошных роликах: «Можно прочитав книгу за 50 рублей потом на ней кормиться всю жизнь. Людям лень читать, им проще заплатить 50 000 руб за ваш семинар и попросить разжевать материал, чем самим читать книгу за 50 рублей».
Справедливости ради нужно отметить, что книга Саймона Вайна стоила порядка 1200 руб, семинары по опционам я проводить не собираюсь (хотя уже начинают приглашать), целью прочтения книги я ставил желание поближе познакомиться с опционами и научиться на них зарабатывать. Обучать людей нет никакого желания, ни возможности, нужно двигаться дальше самому.
Ставлю новую цель — добить до конца этого года книгу Шелдона Натенберга.
Когда ты ставишь цель и достигаешь потом ее — наступает невероятное чувство эстетического удовольствия. Ты говоришь сам себе: «да, я смог, не сломался в пути и не свернул с этой цели». Это очень круто.
Завершить свои топики по книге Саймона Вайна я хотел бы приложением «моделирование», где даются формулы для расчёта опционов.
Тру-опционщик должен знать всего лишь 3 формулы, с помощью которых он потом сможет крутить весь мир вокруг своей оси.
Формула №1: Цена опциона колл на бездивидендную акцию по модели МБШ
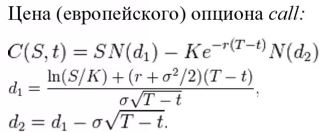
Формула №2: паритет между ценой опциона колл и пут
С + K*e^(-r*(T-t)) = P + S
Из формулы №1 и формулы №2 получаем формулу №3: Цена опциона пут на бездивидендную акцию по модели МБШ
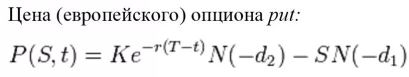
N (d1) и N (d2) — это функция нормального распределения от числа, встроена в Excel, нужно набрать «нормрасп» с параметрами (d1;0;1;1), где d1 — это то самое число, функцию нормального распределения от которого мы считаем, 0 — мат.ожидание, 1 — стандартное отклонение, 1 — признак интегрального исчисления, который нам даёт вероятность:
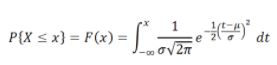
Необходимо также запомнить, что N(d2) в МБШ — это вероятность того, что опцион с конкретным выбранным страйком будет исполнен.
Если будет время, напишу как-нибудь статью на Яндекс-Дзене как выводится МБШ. Если разобраться какой смысл придается каждому элементу из формулы, то МБШ заиграет новыми красками и расчёты начнут приносить удовольствие.
Любите опционы.
С уважением, Карлсон.
---
p.s. кому интересно, свои мысли по рынку кидаю в канал «Фондовый рынок глазами Карлсона» (t.me/KarLsoH), там же есть и опционный чат.
теги блога KarL$oH
- karpov72
- Ri
- S&P500
- S&P500 фьючерс
- Seven_17
- Si
- US500
- zorro
- Алроса
- армагеддон
- Армагедон будет но чуть позже
- аукцион закрытия
- АФК Система
- Бабочки
- башнефть преф
- биткоин
- Блэк-Шоулз
- Валеев Ренат
- Ванга
- Василий Олейник
- Вася Олейник
- веселый молочник
- Вестников
- Витя
- Высшее образование
- Газпром
- гуру
- гусев в.п
- Джордж Сорос
- Доллар рубль
- еженедельные опционы
- ждун
- золото
- Игры разума
- ИгРы РаЗуМа 2020
- иГРЫрАЗУМа
- иГРЫрАЗУМа 2019
- иГРЫрАЗУМа 2020
- иГРЫрАЗУМа2018
- иис
- инвесторы
- Коровин
- коэффициент Шарпа
- красный циркуль
- кризис 2020
- кукл
- Лукойл
- лчи
- ЛЧИ 2018
- ЛЧИ 2019
- лчи 2021
- ЛЧИ 2022
- Магнит
- маржин колл
- Мартынов
- математика на рынке
- медвежий рынок
- ММВБ
- мобильный пост
- мозг трейдера
- нетленочка
- Нефть
- новичкам
- обучение
- опрос
- Опционный чат
- опционы
- Опционы для новичков
- опционы для чайников
- опционы новичкам простыми словами
- открытие брокер
- оффтоп
- подкормка для плотвы
- попрошайка
- потеря денег
- промсвязьбанк
- психология трейдинга
- Распадская
- рецензия на книгу
- роботы
- Ростелеком
- Ростелеком а.о
- РТС
- Русагро
- сбербанк
- ситуация на текущий момент
- смартлаб
- Солодин Дмитрий
- Тарасов
- теханализ
- трейдинг
- тролли
- улыбка волатильности
- Управление портфелем активов для Алексея
- управление портфелем ценных бумаг
- ФСК Россети
- фьючерс ртс
- хомяк
- черная метка
- шорт - дело веселое



















Говорят, что ещё кур доят. Но я не об этом!
А вы видите смысл читать отдельно Вайна, Натенберга, МакМилана? Ведь по сути про одни и те же модели примерно одно и тоже пишут? Ну да МакМилан по попсовее, зато доступнее для многих… но уж Вайн и Натенберг видятся как почти полное объединение множеств
Что-то мне подсказывает, что после Саймона и Натенберга уже можно по опционам ничего больше не читать, но Макмилана тоже посмотрю обязательно, его часто расхваливают.
Саймон Вайн вообще из России, но писал книгу на английском и она вошла в список рекомендованной литературы ряда западных университетов, включая Кембридж.
Сейчас опционный рынок в РФ — это вообще жалкое подобие того, что есть на западе. На Америке можно торговать опционные конструкции сразу, задав, например, параметры для кондора и брокер весь кондор соберет целиком. В РФ такого нет, тут и ликвидности нет и вообще кроме Ri больше ничего торговать нельзя толком, иначе спрэды по 20% заберут львиную долю от прибыли.
Мне понравилось в конце как Саймон пишет про сложны опционные формулы:
Ты знаешь, что нужно делать))
Не, я лучше в сторонке постою
Кот один остался, кто ещё ничерта не смыслит в этих штуковинах греческих