Блог им. imagic
Облигации: мифы и реальность. Часть 3 Глава 4.2.1 Обсуждение некоторых стратегий на рынке облигаций
- 22 ноября 2022, 20:39
- |
(окончание, начало здесь)
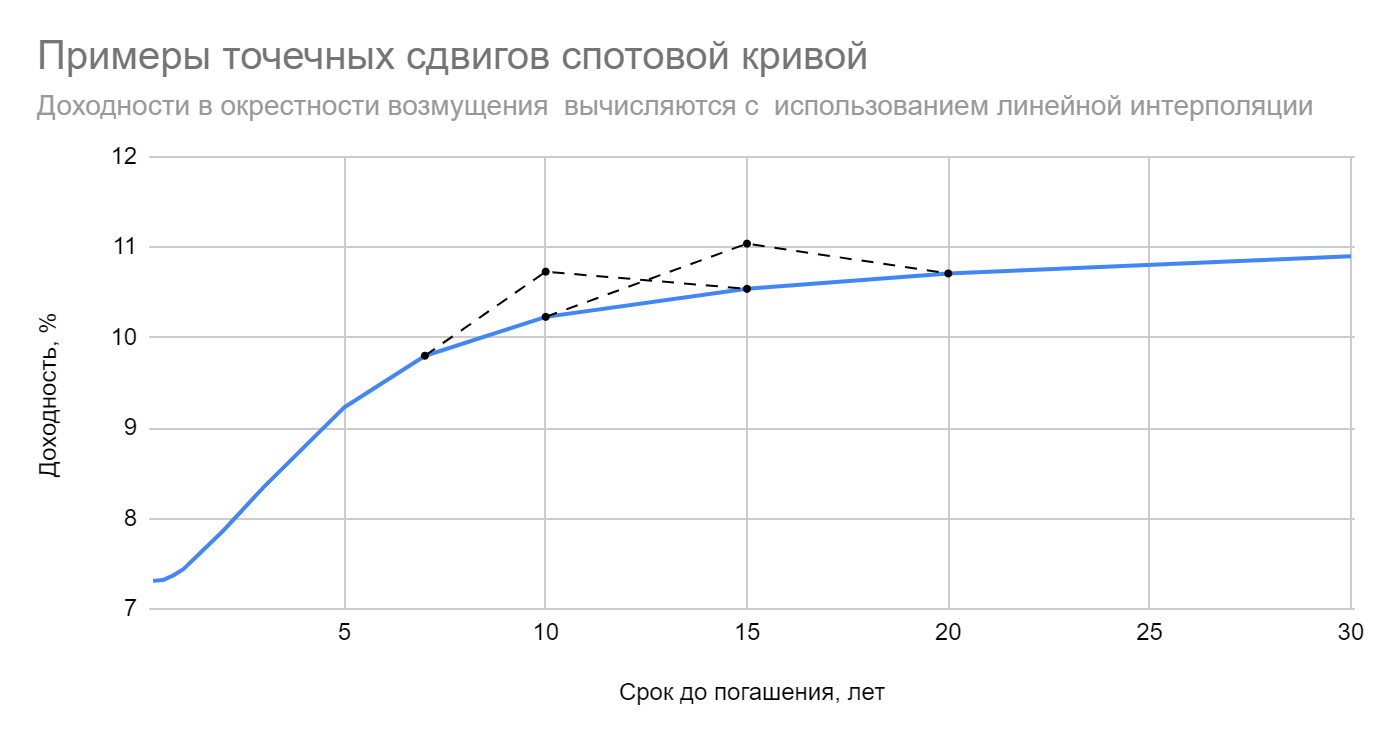
Обычно выделяют несколько типов изменения спотовой кривой: параллельный сдвиг, изменение наклона и изменение кривизны. Примеры таких трансформаций приведены на рисунке:
В частности, параллельный сдвиг происходит тогда, когда спотовые ставки изменяются на одну и ту же величину. Если ставки по коротким облигациям вырастут сильнее, чем по длинным, говорят об уплощении (уменьшении наклона) КБД, и так далее. Понятно, что реальное движение кривой представляет собой некоторую комбинацию всех указанных типов смещений. У инвесторов и аналитиков сложилась своеобразная классификация этих типов: {bear/bull} {steepening/flattening}; positive/negative butterfly
Например, медвежье уплощение (bear flattening) — движение спотовой кривой вверх с одновременным уменьшением наклона. Положительный баттерфляй (positive butterfly) связан с уменьшением кривизны временной структуры, т.е. она становится менее сгорбленной. Если при этом кривая сдвигается вверх, то короткие и длинные ставки растут быстрее, чем среднесрочные. При движении кривой вниз всё происходит с точностью наоборот: среднесрочные ставки снижаются сильнее.
Обозначим доходности по коротким, среднесрочным и длинным облигациям как YTM(S), YTM(L), YTM(L) соответственно. Наклон кривой доходности принято измерять спредом кривой доходности:
yield spread = YTM(L) — YTM(S)
а ее изгиб спредом “баттерфляй”:
butterfly spread = — YTM(S) + 2∙YTM(M) — YTM(L)
В зависимости от целей исследования могут выбираться разные значения срочности облигаций для спредов: 2 — 10, 2 — 30, 0.25 — 5 — 10, 2 — 10 — 30 и т. д.
Раз уж мы отошли от использования YTM и его приращений при оценке ожидаемой доходности, нам следует уточнить понятие дюрации (модифицированной дюрации) для портфеля облигаций. Будем считать, что дюрация, как мера ценового риска, это чувствительность стоимости P портфеля к параллельному сдвигу КБД. Пусть все спотовые ставки мгновенно изменились на одну и ту же величину Δs. Тогда определим дюрацию портфеля Dₚ следующим образом:
Dₚ = — 1/P ∙ ΔP/Δs
Поскольку портфель можно рассматривать как совокупность бескупонных облигаций (рассматривая отдельно купоны и номиналы входящих в него бумаг), то легко показать, что определенная таким образом дюрация будет равна средневзвешенному значению дюраций составляющих его элементов. Если xᵢ — стоимость i-го актива в портфеле, то P = Σ xᵢ, ΔP = Σ Δxᵢ, где Δxᵢ —изменение стоимости i-го актива, Dᵢ = — 1/xᵢ ∙ Δxᵢ/Δs. Поэтому Dₚ = Σ xᵢDᵢ/P Данное равенство примерно выполняется и в случае, если в качестве xᵢ и Dᵢ взять цены и модифицированные дюрации самих облигаций (без разделения на купоны и номинал) Это особенно удобно, так как дюрации указаны во многих трейдерских приложениях и на сайте Мосбиржи (там нужно выбирать модифицированную дюрацию), т.е. их не нужно вычислять самостоятельно. Важно в данном подходе помнить две вещи:
- варьируется вся спотовая кривая, а не YTM портфеля.
- временная структура сдвигается параллельно.
В уже упомянутой книге Ф. Фабоцци “Рынок облигаций. Анализ и стратегии” при определении дюрации используется сдвиг обычной кривой доходности. В некоторых других своих работах Фабоцци говорит о сдвигах спотовой кривой. Определенная так или иначе дюрация портфеля всё равно будет равна средневзвешенной дюраций отдельных денежных потоков/облигаций, так как существенно только то, что доходности — будь это спотовые ставки или YTM купонных облигаций — изменяются на одну ту же малую величину. И всё же инвестору желательно использовать единый подход.
На рис. ниже изображены две модельные кривые: КБД (спотовые ставки) и соответствующая ей (безарбитражная) кривая доходности для облигаций со ставкой купона 20%. Ставка нарочно взята высокой, чтобы доходности реально торгующихся облигаций заведомо попадали в область между кривыми. Портфель инвестора представлен тремя облигациями, две из которых имеют относительно низкий купон по сравнению с третьей (8-ми летней) Этот портфель инвестор выбирает самостоятельно и может считать набор из 3-х точек на рис. своей личной “кривой доходности” Но параллельный сдвиг этой “кривой” не означает, что и любая другая комбинация точек внутри области, соответствующая произвольному портфелю, сдвинется параллельно, или наоборот. Инвестору могут быть не известны статистические свойства и корреляции доходностей выбранных им облигаций и его портфель не должен быть универсальным бенчмарком для всех остальных.
Поэтому в своем определении дюрации портфеля мы и останавливаемся на КБД. Аналогичные рассуждения при параллельном сдвиге спотовой кривой можно провести и для выпуклости. Выпуклость портфеля будет равна средневзвешенному значению выпуклостей составляющих его облигаций.
Как мы уже упомянули, изменение формы спотовой кривой бывает и другим — например, ее наклон может увеличиваться так, что короткие ставки снижаются, а длинные растут. Такая возможность приводит к структурному риску или риску формы кривой доходности. В этой ситуации используют так называемые частные дюрации (partial durations, key rate durations). Для их вычисления на спотовой кривой выделяют несколько точек, обозначаемых как ключевые ставки (key rates) Чаще всего они выбираются для характерных сроков до погашения, аналогично тому, как ЦБ и Мосбиржа разбивают КБД: 0.25, 0.5, 1, 2, 3, 5 и т.д. лет.
На рис. ниже приведена Кривая бескупонной доходности государственных облигаций, построенная по данным за 18 ноября 2022.
Если, например, сдвинуть 10-летнюю спотовую ставку на Δs₁₀, частная дюрация для этой точки кривой рассчитывается так:
D₁₀ = — 1/P ∙ ΔP₁₀/Δs₁₀, где ΔP₁₀ — изменение стоимости портфеля в результате этого сдвига.
Сумма всех частных дюраций будет равна дюрации портфеля (как мы ее определили выше для параллельного сдвига кривой) поскольку для точек, соседних с точкой сдвига, используется линейная интерполяция. Если все Δsᵢ = Δs, графическая сумма прямых в любой точке даст такое же значение сдвига, что эквивалентно параллельному смещению кривой.
В качестве примера рассмотрим некоторый портфель с частными дюрациями [D₀.₂₅, D₀.₅, …, D₃₀], соответствующими 12-ти срокам до погашения (какие обычно использует ЦБ РФ): [0.25, 0.5, …, 30] Допустим, что КБД повернулась относительно точки с абсциссой 7 лет так, что для каждого
i = 0..11: sᵢ = δ∙(—3.5+ i∙0.5).
На рис показано изменение формы спотовой кривой для δ = 25 б.п.:
Тогда приближённое изменение стоимости портфеля будет равно
ΔP/P = —[D₀.₂₅∙(— 3.5∙δ) + D₀.₅∙(— 3∙δ) + … + D₃₀∙(+2∙δ)]
Всё бы хорошо, но считать 12 отдельных частных дюраций вместо одной модифицированной — работа довольно утомительная (возможно, придется использовать программное обеспечение) Конечно, такой набор позволит рассчитать огромное количество различных сценариев движения кривой, но далеко не все из них будут типичными. В этой связи возникает вопрос: какие трансформации КБД разумно исследовать при составлении прогноза? Справедливо ли исходить из того, что процентные ставки скачут хаотично? Или их влияние на стоимость портфеля можно свести к небольшому ряду факторов?
По счастью, доходности ОФЗ не изменяются совсем уж произвольно и независимо друг от друга. В каком-то смысле вся КБД напоминает упругий прутик, имеющий собственные частоты: ставки по облигациям с близкими сроками до погашения обладают высокой положительной корреляцией.
Согласно историческим данным по бескупонным доходностям ОФЗ за 2013-2022 гг. можно составить матрицу этих корреляций:
Видно, что степень взаимосвязи между ставками любой срочности составляет не менее 75%, что и позволяет рассматривать КБД как единое целое. Трудно представить ситуацию, когда, например, 3-летние ставки выросли на 100 б.п., а 5-летние упали на ту же величину. Скорее всего они “потянутся” вслед за соседками.
Для снижения размерности взаимосвязанных данных без существенной потери информации широко используется метод главных компонент. Он позволяет уменьшить число переменных, выбрав самые изменчивые из них. Его математическая идея довольно проста: это создание новых переменных (как линейной комбинацией старых) таким образом, чтобы первые из полученных переменных впитали в себя практически всю изменчивость. Первая главная компонента должна иметь максимальную выборочную дисперсию. Вторая главная компонента подбирается так, чтобы с одной стороны она была не коррелирована с первой, а с другой также имела максимальную выборочную дисперсию из возможных; и так далее. Данный процесс чем-то напоминает последовательное выделение сигнала из шума и позволяет в случае измерения рисков смещения КБД свести число основных факторов к двум или трём.
На рис. ниже изображены первые три главные компоненты для приращений бескупонных доходностей ОФЗ по данным за 2013-2022 гг.
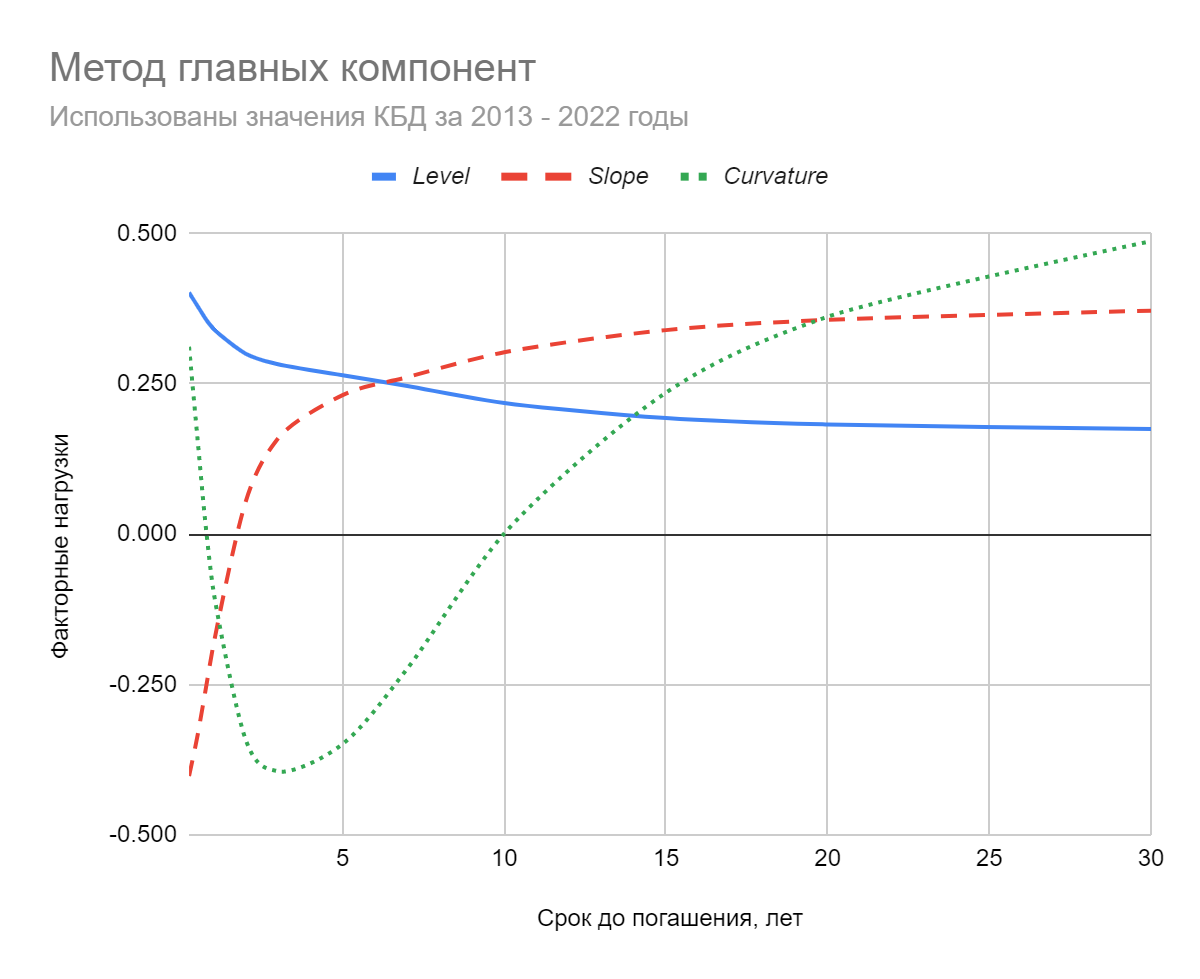
Из рисунка видно, что первая главная компонента PC1 (level) примерно соответствует параллельному сдвигу КБД, вторая PC2 (slope) — отвечает за наклон кривой, а третья PC3 (curvature) связана с изгибом КБД. Из данных за 2013-2022 гг. также следует, что PC1 объясняет почти 85% всей дисперсии, PC2 — 9%, а PC3 — 4%. Общая дисперсия, приходящаяся на первые три главные компоненты составляет около 98%
Говоря простыми словами, подавляющая часть движений КБД с достаточной для практических целей точностью может быть аппроксимирована комбинацией первых трёх факторов. Т.е., вполне естественным будет, например, прогноз: КБД как целое сдвинулась вверх, стала более плоской, а ее кривизна уменьшилась. А значит, жизненные наблюдения трейдеров и аналитиков, использующих описанную ранее классификацию — bull/bear/flattening/steepening/butterfly — имеют под собой твёрдую статистическую основу.
Кроме того, указанные три видоизменения кривой не вполне независимы друг от друга. При сдвиге спотовой кривой вверх она имеет тенденцию уплощаться и уменьшать кривизну. И, наоборот, когда ставки в целом снижаются, наклон КБД увеличивается и она становится более “сгорбленной” Так происходит потому, что краткосрочные ставки обычно показывают большую волатильность, чем долгосрочные: при любом сдвиге кривой короткие ставки стремятся “опередить” длинные. Это видно и по графику для PC1 — кривая факторных нагрузок для небольших сроков до погашения загибается вверх; при одинаковой волатильности ставок линия была бы горизонтальной.
Таким образом, метод главных компонент позволяет свести число анализируемых факторов до трёх и мы можем ввести новые меры риска для портфеля — факторные дюрации:
Dⱼ = — 1/P ∙ ΔP/Δθⱼ
где θ₁, θ₂, θ₃ — факторы, отвечающие за сдвиг, наклон и кривизну соответственно.
Увеличение первого фактора θ₁ приводит к тому, что доходности для различных сроков вырастут примерно на одну и ту же величину. Повышение θ₂ означает, что краткосрочные ставки снизятся, а долгосрочные вырастут, т.е. спред кривой доходности увеличится и т.д. Таким образом, факторная дюрация D₁ аналогична определенной выше модифицированной дюрации портфеля, а D₂ и D₃ — носят характер чувствительности к изменению спреда кривой доходности и к спреду “баттерфляй”.
Факторные дюрации обладают тем же замечательным свойством, что и обычные: факторная дюрация портфеля равна средневзвешенному значению факторных дюраций составляющих его активов.
Теперь, используя описанный выше факторный подход, можно упростить выражение для примерного изменения стоимости портфеля в результате общего сдвига КБД:
ΔP/P = —D₁∙Δθ₁ — D₂∙Δθ₂ — D₃∙Δθ₃
Когда мы обсуждали стратегии на базе ожидания изменения общего уровня процентных ставок в экономике (duration strategies), то не придавали большого значения тому, облигации какой срочности входят в состав портфеля. Фактически, мы просто рассматривали конкретную дюрацию и регулировали ее согласно прогнозам о направлении движения ставок. Внимательный инвестор быстро обнаружит, что одну и ту же дюрацию при фиксированном размере капитала можно получить разными способами. Один из них, например, — вложить всю сумму в облигации с близкими сроками до погашения. Альтернативой будет приобрести бумаги различной срочности, разместив в них те же средства в определенной пропорции, чтобы получить такую же дюрацию, как и в первом случае. На практике состав портфеля может быть самым пёстрым, но чаще всего используется три основных типа:
1) bullet (“буллетный”) 2) barbell (“барбелл”) и 3) ladder (“лестничный”)
Они схематично изображены на рисунке и не требуют особых пояснений.
В “буллетном” портфеле используются облигации, у которых срок до погашения концентрируется вокруг одной даты. У “барбелла”, наоборот, эти сроки сильно разнесены. “Лестница” напоминает аннуитетные платежи: в портфеле примерно в равной пропорции присутствуют облигации для всех сроков до погашения. В источниках это равенство пропорций трактуется по-разному: некоторые, как Фабоцци, пишут, что это одинаковое количество бумаг — т. е., например, 10 облигаций сроком в один год, столько же двухлеток и так далее. Другие авторы говорят о равенстве денежных вложений, т.е. стоимостной оценке: вложить 10 тыс. руб. в годовые, столько же в двухлетки и т.д. О различиях этих двух подходов мы поговорим позднее, но заметим, что они совпадают, если облигации приобретены за номинал.
Методы управления портфелями фиксированной дюрации носят название стратегий кривой доходности (yield curve strategies, yield curve trades with a neutral duration view) Они сосредоточены на возможности извлечения прибыли из деформаций КБД для комбинаций портфелей, имеющих одинаковую стоимость и дюрацию, но разные выпуклость и чувствительность к непараллельным сдвигам. Пример такой комбинации — стратегия “баттерфляй”, т.е. покупка “барбелла” и продажа “буллета” Она имеет в силу построения нулевые затраты и при определенных движениях КБД может принести некоторый доход.
Если мы рассматриваем мгновенные изменения нормальной (возрастающей) кривой доходности, т.е. сразу после покупки облигаций, то при малых параллельных смещениях эти три портфеля сработают примерно одинаково, поскольку у них одни и те же дюрация и стоимость. Выпуклости портфелей однако различны; их можно ранжировать по возрастанию: “буллетный” < “лестничный” < “барбелл” В силу этого при относительно больших параллельных сдвигах КБД лучший результат покажет “барбелл”: по сравнению с остальными его стоимость при снижении ставок вырастет больше и упадёт меньше при их росте. Поэтому ожидающий сильного движения трейдер может реализовать стратегию “баттерфляй”, чтобы получить доход вне зависимости от направления движения ставок. Потенциальный заработок тем выше, чем больше сдвиг и чем менее вогнутой (более выпуклой) является спотовая кривая (о различных формах кривой подробнее говорилось в этой главе)
Влияние формы КБД на результативность данной стратегии нельзя недооценивать. Дело в том, что средневзвешенная доходность “барбелла” всегда ниже, чем у “буллета” той же дюрации и стоимости, если КБД имеет нормальную форму. Мы уже обсуждали в прошлых частях, что именно такая форма препятствует арбитражу в стратегии “баттерфляй” Для реализации своего преимущества “барбелл” должен преодолевать эту “нехватку” доходности. Более того, если КБД остается неизменной продолжительное время, однопериодный HPR “буллетного” портфеля будет выше, чем у “барбелла”, т.к. эффект большей выпуклости “барбелла” со временем истощается (продолжая наши аналогии с деривативами, ситуация напоминает тета-распад стоимости опциона, если базовый актив остается без движения) А это значит, что для сохранения прибыльности стратегии “баттерфляй” понадобятся еще более серьезные сдвиги КБД в конце срока удержания позиции.
В следующем примере мы используем уже привычную временную структуру из прошлой части:

дальнейшие выкладки могут показаться слишком подробными, но они полезны для понимания механизма расчетов и навыков работы с таблицами
Допустим, мы вложили 100 д. е. в покупку 5-летних бескупонных облигаций и составили таким образом “буллетный” портфель (обозначим его латинской буквой B) Средневзвешенная доходность портфеля B равна 5-летней спотовой ставке, т.е. y(B) = 6.164% При ежегодном начислении процентов его модифицированная дюрация D(B) = 5/(1+y(B)) = 4.71 Построим эквивалентный по дюрации портфель “барбелл” из облигаций A и С сроками до погашения в 1 год и 10 лет. Для этого нам придется решить простое уравнение:
D(B) = D(A)∙x + D( C)∙(1-x)
где дюрации облигаций A и С равны соответственно D(A) =1/(1+4.5%) = 0.957; D( C) = 10/(1+6.918%) = 9.353
Из уравнения получим веса облигаций A и С в “барбелле”: x = 0.553 (вес А), 1-x =0.447 (вес C) Иными словами, в облигацию A мы вложим 100∙x = 55.3 д. е., а в С — 100∙(1-x) = 44.7 д. е. Легко проверить, что средневзвешенная дюрация “барбелла” равна дюрации “буллета”, а стоимости портфелей совпадают. Средневзвешенная доходность “барбелла” будет ниже, чем у “буллета”: 5.581% против 6.164%. Эти средневзвешенные доходности, конечно, не определяют ожидаемые через год HPR портфелей, но позволяют их качественно сравнить: если y₁ < y₂, то и НРR₁ < HPR₂ (при допущении, что КБД не изменится)
“Номинальные” стоимости облигаций (face values) легко получить с помощью формул из Excel или Google Таблиц. Например, FV(B) = FV(6.164%, 5, 0, — 100) = 134.86. Т.е., вложив сегодня 100 д.е. в облигацию B, через 5 лет мы получим 134.86 д.е. Эти стоимости нужны для дальнейшей оценки судьбы портфелей. Если все спотовые ставки после составления позиции мгновенно увеличатся на 100 б.п., то стратегия “баттерфляй” принесёт пусть и скромную, но прибыль:
PV(5.5%, 1, 0, —FV(A) ) + PV(7.918%, 10, 0, —FV( C) ) — PV(7.164%, 5, 0, —FV(B) ) = 0.08 или 8 б. п. от суммы вложенного.
Но если КБД не изменится по прошествии года, трейдер будет вынужден зафиксировать убыток от стратегии:
FV(A) + PV(6.829%, 9, 0, —FV( C) ) — PV(5.878%, 4, 0, —FV(B) ) = —1.38
А для того чтобы “баттерфляй” через год вышел в положительную зону, понадобится параллельный сдвиг КБД уже не менее 200 б. п.
Сходный анализ можно провести и для непараллельных сдвигов кривой доходности. Если кратко суммировать итоги, то в конце удержания позиции для спотовой кривой нормальной формы:
- При небольшом параллельном сдвиге буллетная стратегия предпочтительней, но при достаточно сильном смещении “барбелл” покажет себя лучше
- При уплощении кривой (уменьшении спреда доходности) портфель “барбелл” всегда переигрывает “буллет”
- При росте наклона кривой доходности “буллетная” стратегия предпочтительней, если увеличение спреда достаточно велико
- Увеличение спреда “баттерфляй” повышает привлекательность стратегии “барбелл”, а его уменьшение — “буллетной”
- “Лестничный” портфель во всех случаях покажет промежуточные результаты между “буллетом” и “барбеллом”
Следует подчеркнуть, что стратегии кривой доходности:
а) Требуют при составлении портфелей придерживаться одной дюрации, что имеет смысл в случае, если инвестор следует определенному индексу или заинтересован в хеджировании текущей позиции б) Подразумевают короткие продажи (шорт) облигаций, возможность чего для большинства инвесторов недоступна. В этом могли бы помочь фьючерсы на корзину ОФЗ, но они куда-то подевались из стаканов и когда вновь появятся неизвестно. Более того, для неопытного инвестора использование фьючерсов не целесообразно. Фьючерсы на облигации, тем более на корзины, сложнее обычных и их ценообразование не всегда прозрачно в) Если и когда приносят доход, то его размер относительно невелик, а риски существенны.
Использование чистых портфельных стратегий (только “барбелл” или “буллет”) далеко не всегда даст нужный результат, среди них трудно выявить победителя. Когда нам говорят, что вот этот портфель ведёт себя лучше при прочих равных, чем другой, нам нужно проверить, не стоит ли изменить эти “равные”, прежде чем выбрать “хороший” портфель. Зачем строить “барбелл” при уплощении кривой, если ожидается, что ставки при этом пойдут вверх? Возможно, правильнее будет снизить дюрацию портфеля. Существует ли наилучшая стратегия при всём разнообразии возможных сценариев? Такая стратегия на все случаи жизни общеизвестна и носит имя М. Орловского — сидеть в кэше и ждать у моря погоды. Инвестору придется сформировать целевой прогноз, чтобы составить оптимальный портфель. Отдельно стоит отметить ситуацию с уплощением кривой — при одновременном движении КБД вниз “барбелл” однозначно предпочтительнее буллета, однако как назло, именно при снижении ставок КБД имеет тенденцию к увеличению, а не уменьшению своего наклона.
В заключение этого раздела представляем анимацию, описывающую динамику КБД за 2013-2022 г.г. Визуальный анализ зачастую позволяет выявить какие-то характерные закономерности, сделать важные наблюдения, да и вообще как-то успокаивает.
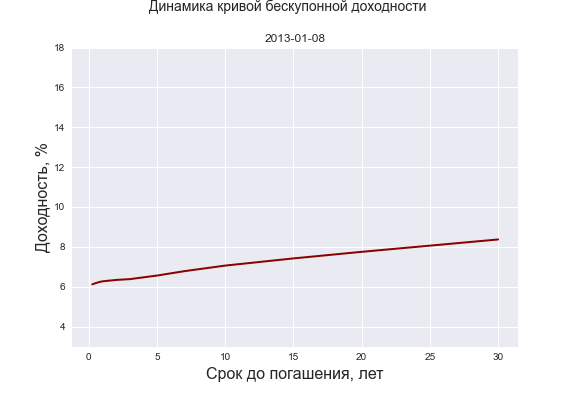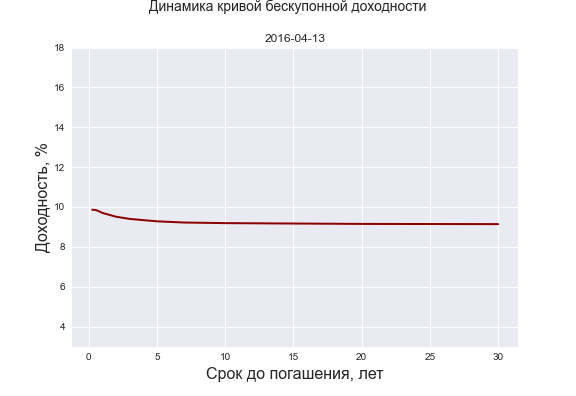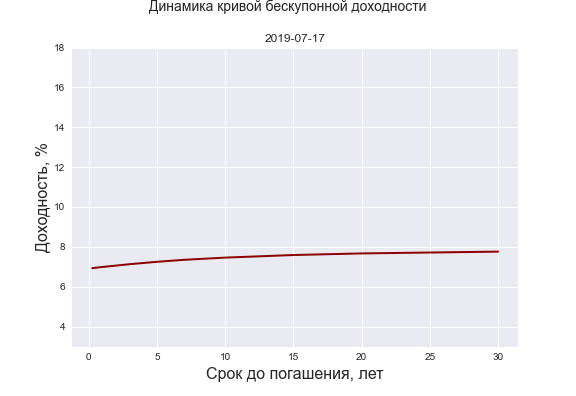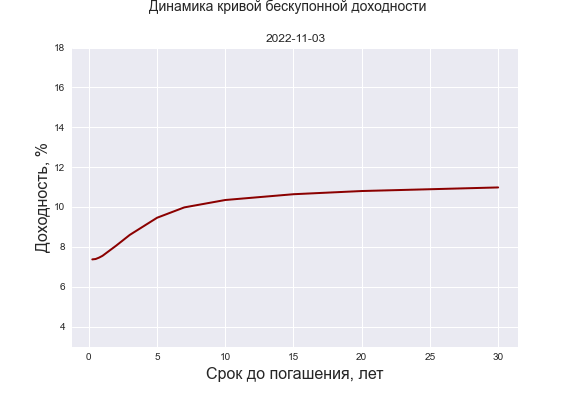
Также публикуем код в Python для импорта данных по значениям КБД и ключевой ставки с сайта ЦБ РФ, который будет полезен инвесторам для проведения самостоятельных исследований в области инструментов процентного дохода.
В следующем разделе мы вкратце обсудим политики управления портфелями облигаций, если горизонт инвестирования составляет свыше одного купонного периода.
- 22 ноября 2022, 23:49

- 22 ноября 2022, 23:54

- 24 ноября 2022, 12:06

теги блога Tenant
- 90-ые
- ChatGPT
- fixed income
- python
- RGBI
- акции
- амортизация облигаций
- анализ облигаций
- Арсагера
- Атомэнергопром облигации
- Банк России
- банковские вклады
- Бинарный опцион
- биржевые облигации
- Блэк-Шоулз
- Бюджетное правило
- Великая Отечественная война
- вечный портфель
- вклады и инвестиции
- ВТБ
- Газпромбанк
- головоломка
- гурам на заметку
- Дерипаска
- дивиденды
- доллар
- доллар рубль
- доходности облигаций
- доходность
- дуэль
- дюрация
- зеленый слоник
- золотишко
- игра
- игра в кальмара
- инфляция
- ключевая ставка
- Ключевая ставка ЦБ РФ
- кривая доходности
- курс доллара
- линкеры
- лира
- Мавроди
- математика
- Минфин
- МММ
- МосБиржа
- мы победим
- налог на депозиты
- налоговая реформа
- НДФЛ
- Норникель
- Облигации
- обратные флоатеры
- ожидаемая доходность
- опрос
- опционная комбинация
- открытие брокер
- ОФЗ
- офз с амортизацией долга
- оффтоп
- оценка активов
- повышение НДФЛ
- популяризация
- Потанин
- прогрессивная шкала налогообложения
- производные финансовые инструменты
- промсвязьбанк
- Пульс
- ПФИ
- рост цен на бензин
- рубль
- Русгидро
- Сбербанк
- Свет в конце тоннеля
- Селигдар
- сложный процент
- ставка ФРС США
- стратегии
- стратегии инвестирования
- Структурные продукты
- теорвер
- теория вероятностей
- теория игр
- Тинькофф
- торговые роботы
- учебный материал
- флоатеры
- фонды облигаций
- форвард
- форекс
- человеческий капитал


















