Используя простые модели волатильности, рассчитанные по ценам закрытия (Close-to-Close vol.) мы неизбежно сталкиваемся с рыночным шумом, смещающим наши оценки далеко её от истинного или асимптотического значения.  Мы могли бы измерять волатильность как-то иначе, например по модели Паркинсона (High-to-Low 1980), но столкнулись бы с той же проблемой. 



 

1.1 — Close to Close log-volatility estimation





( Читать дальше )

Игра в угадайку — она как стрельба: можно угадывать точно, а можно угадывать кучно. 




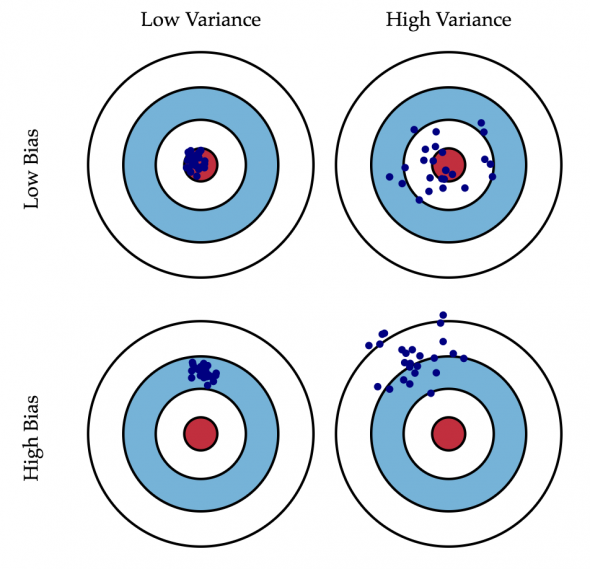
Иллюстрация. 1 и 2 столбец — кучная и не-кучная угадайка, 1 и 2 строка — точная и не-точная угадайка. 

Аналогично и с угадыванием волатильности. 



Лучше, конечно, вообще не угадывать волатильность, лучше её предсказывать, а ещё лучше — измерять или просто знать. Поэтому, мы будем волатильность не угадывать, а измерять, чтобы наш арбитраж, который мы собираемся над ней совершить, выглядел бы соответственно. А измерять волатильность мы будем в предположении Блэка-Шоулза о лог-нормальном распределении приращений цены актива-подложки, и потому будем пользоваться специально припасёнными математиками для этого случая инструментами: среднеквадратичным отклонением — СКО. Но измерять волатильность мы будем тоже не просто так — не просто в лоб по СКО, а GARCH методом, предполагающим, что чем дольше мы измеряем нечто, тем точнее у нас это получается. Мы же не просто измеряем всё-таки, а делаем это весьма интеллектуально! 

( Читать дальше )

По мотивам последних обсуждений.






Куда унесёт нас ураган? Выдержат ли паруса? Оставит ли в живых злая буря свою новую игрушку? Так спрашивает себя каждый капитан перед дальним плаванием, расслабившись за игрой в орлянку.




( Читать дальше )

Сегодня мы будем выступать в качестве поставщика бесконечной ликвидности по опционам. То есть мы будем безотказно играть в игру с нулевой суммой так, чтобы, как минимум, не проиграть, а это возможно только в том случае, если мы будем продавать и покупать волатильность по цене, соответствующей седловой точке в игре покупателя и продавца, то есть по цене GTO (game theory optimal). Иными словами, мы будем заниматься непосредственно pricing'ом опционов, назначая цены put'ам и call'ам, таким образом, чтобы ни одна стратегия и ни один набор случайных, стохастических стратегий не мог получить положительное преимущество при игре с нами.

Чтобы назначать цену волатильности, для начала, не плохо было бы принять какую-либо модель волатильности. Например, это может быть модель случайного процесса, подчинённого логистическому распределению:


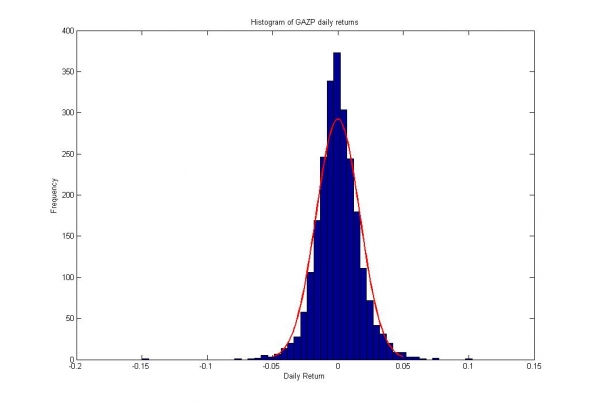
Рис.1. Распределение логарифмических приращений цен акций ПАО Газпром и их аппроксимация логистическим распределением.


или распределению Лапласа:

( Читать дальше )

Занимаясь первоначально исключительно портфельным инвестированием мы всё чаще сталкиваемся с задачей моделирования волатильности фондового рынка и его будущих ковариаций. Соответственно,  так или иначе, мы сталкиваемся с проблемой выбора модели, которая позволяла бы нам на самом широком диапазоне данных получать сколько-нибудь значимые оценки. 


В качестве показателя качества моделей нами была выбрана доля объяснённой дисперсии:





и промоделирована ошибка измерения волатильности заданного стационарного процесса на интересующем нас интервале: 




( Читать дальше )