Для того, чтобы продать волатильность, нам необходимо продать стрэддл — этим, мы полностью избавляемся от чувствительности к направлению движения цены, оставляя при этом чувствительность к «волатильности»… Чтобы не запутаться, обозначим первую волатильность за IV (Implied Volatility) и будем считать  её заранее известной и эффективной. 


Если бы рынок был монеткой и выходил бы на экспирацию двумя возможными вариантами {+IV, -IV }, то результатом продажи нашей опционной конструкции был бы ровно 0, в силу равенства IV=RV. Но рынок выходит на экспирацию через «тренды» и «пилы», которые выводят Базовый Актив в том числе далеко за ± IV, и в том числе и в ноль.  В результате, конечное отклонение от ± IV  и, соответственно, риски, которые мы принимаем при продаже стрэддла, составляют приблизительно :



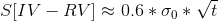
где S — СКО, RV ( «реализованная волатильность»)   - отклонение цены на экспирацию, t — время до экспирации, а сигма0 — величина шага движения цены. Это уравнение можно получить численно, а можно, взяв интеграл по соответствующему распределению Гаусса (аналитический вариант).  

( Читать дальше )

Каждый учебник предлагает нам простой и эффективный метод извлечения прибыли — репликация опциона при помощи фьючерса. При чем все, что для этого нужно — всего лишь «не думать и торговать по принципу: растёт — покупай, падает — продавай!».  Всё просто, понятно, бесспорно и… совершенно неверно.

Потому что «не думать» — в процессе погони за прибылью, — на самом деле, сложно. И если вам непонятно, зачем вообще нужны эти опционы, если они так легко реплицируются фьючерсами, то просто брать,  и «не думать», уже не получается. Не думать хорошо после того как вы уже хорошо  подумали, и думать второй раз — как минимум, лень. А с первого раза вообще мало чего получается. Особенно — не думать.


Так бы и закончилось моё дельта-хеджирование не начавшись, если бы оно не было столь модным. А то ещё всякое бывает — не задельта-хеджируешь, а потом скажут, что вот, дескать, «Пастернака не читал, но действия его уже осуждает». Нет, надо всё таки разок попробовать… А то в приличном обществе ещё и засмеют почём зря.

( Читать дальше )

«Настоящее образование включает умение хорошо петь и танцевать».  Платон.



Коллега ch5oh задал парадоксальный, на первый взгляд, вопрос: «как продавая дорого то, что стоит дешево, можно ещё и умудриться проиграть?»
Однако парадоксально он выглядит лишь до тех пор, пока мы остаёмся в рамках косной метафизики, не желающей, и не склонной к диалектическому танцу. 

Для сравнения этих двух подходов — метафизики и диалектики — мы будем рассчитывать Нэш-равновесные цены двух недельных опционов (STO) и моделировать игру покупателя и продавца. В первом случае мы будем исходить из постоянства (авторегрессии) волатильности, пользуясь исключительно текущей HV,  а во втором — из её танца (mean-reverse AR), о котором, как нам кажется, мы знаем чуть более, чем ничего.


* То, что волатильность представляет из себя mean-reverse процесс, подобный движению Орнштейн-Уленбека, неоднократно было показано Дмитрием Новиковым ,

( Читать дальше )

По мотивам последних обсуждений.






Куда унесёт нас ураган? Выдержат ли паруса? Оставит ли в живых злая буря свою новую игрушку? Так спрашивает себя каждый капитан перед дальним плаванием, расслабившись за игрой в орлянку.




( Читать дальше )

Сегодня мы будем выступать в качестве поставщика бесконечной ликвидности по опционам. То есть мы будем безотказно играть в игру с нулевой суммой так, чтобы, как минимум, не проиграть, а это возможно только в том случае, если мы будем продавать и покупать волатильность по цене, соответствующей седловой точке в игре покупателя и продавца, то есть по цене GTO (game theory optimal). Иными словами, мы будем заниматься непосредственно pricing'ом опционов, назначая цены put'ам и call'ам, таким образом, чтобы ни одна стратегия и ни один набор случайных, стохастических стратегий не мог получить положительное преимущество при игре с нами.

Чтобы назначать цену волатильности, для начала, не плохо было бы принять какую-либо модель волатильности. Например, это может быть модель случайного процесса, подчинённого логистическому распределению:


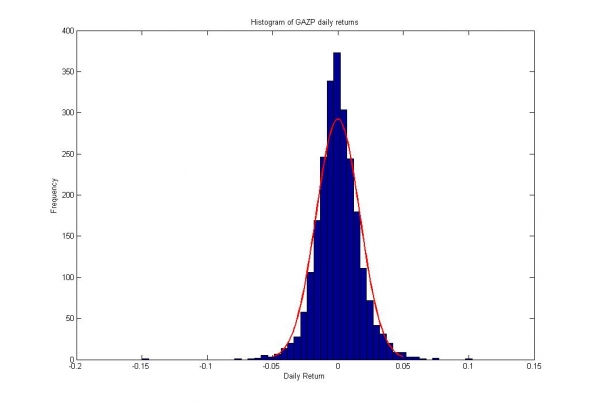
Рис.1. Распределение логарифмических приращений цен акций ПАО Газпром и их аппроксимация логистическим распределением.


или распределению Лапласа:

( Читать дальше )

Вопрос:

Проведена симуляция покупки опционов Call за день до экспирации по страйкам +0%, +2%, +5%, +8% от центрального  — по прогнозным ценам и в целях проверки модели справедливого ценообразования.





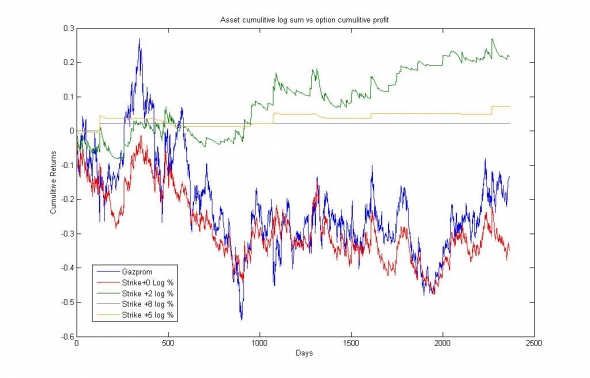
Ev[ +0%] и Ev[ +2%] располагаются на границе доверительного интервала, но по разные стороны.
Требуется ответить на вопрос IV=RV?  Уместен ли t-test?

Занимаясь первоначально исключительно портфельным инвестированием мы всё чаще сталкиваемся с задачей моделирования волатильности фондового рынка и его будущих ковариаций. Соответственно,  так или иначе, мы сталкиваемся с проблемой выбора модели, которая позволяла бы нам на самом широком диапазоне данных получать сколько-нибудь значимые оценки. 


В качестве показателя качества моделей нами была выбрана доля объяснённой дисперсии:





и промоделирована ошибка измерения волатильности заданного стационарного процесса на интересующем нас интервале: 




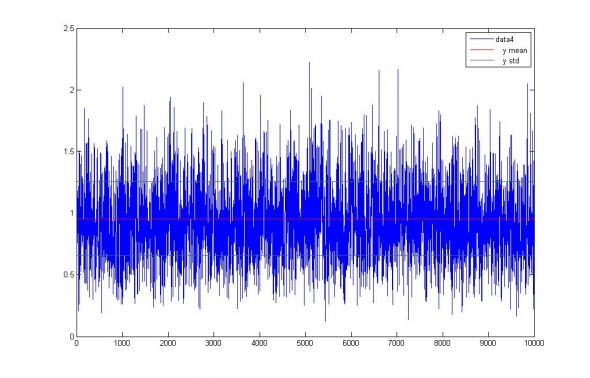
( Читать дальше )

      В свете интереса к моим работам в области оценки рисков нестационарных объектов со стороны опционов и возникшего вопроса о применимости к анализу финансовых временных рядов методов классического статистического анализа проведём маленький численный эксперимент:

• Оценим АКФ акций ПАО Сбербанк за последние 8 лет :

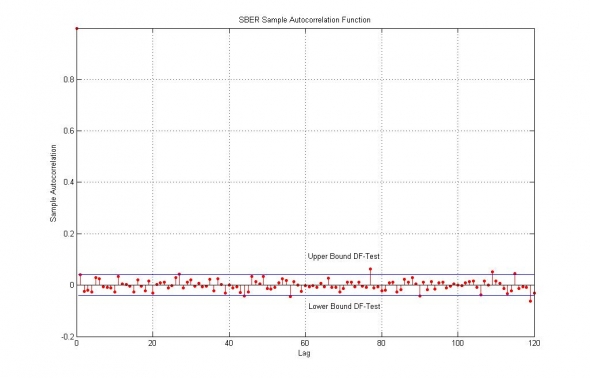
Рис. 1. Тест Дики-Фуллера и автокорреляционная функция логарифмических приращений цен акций ПАО Сбербанк.


Как видно из теста, никаких трендов (англ. тенденций, закономерностей) на акциях Сбербанка классической математической статистикой не обнаружено и все АК коэффициенты лежат в пределе статистической погрешности при измерении нуля.


Однако, тест Дики-Фуллера, с одной стороны, разработан для стационарных, не-локализованных процессов и отражает только отсутствие трендов в среднем по времени, а с другой — проводится совершенно с другими целями выявления детерминированных сезонных и/или растущих тенденций, а не стохастических оценок рисков. В этом смысле мы будем интерпретировать АКФ не по-классически, детерминированно, а как функцию искажения случайности.

( Читать дальше )

Волатильность, как хороший продавец — всегда улыбается своему покупателю. Шутка с долей шутки.


Предположим, что в качестве фундаментального сигнала (событийный ряд) у нас выступает некоторая случайная величина, обладающая следующими «катастрофическими» свойствами:

1. Существует некоторая средняя мощность событий во времени.
2. Если не произошло малого события, то, вероятно, произойдет большое, если не произошло большого, то, вероятно, произойдёт катастрофическое, если не произошло катастрофического — произойдёт ещё более катастрофическое.  Как при землетрясениях и лавинах.
3. Сила события не зависит от уже произошедшей силы события (невозможность скальпинга), то есть отсутствуют ограничения и эффекты памяти для последующего роста мощности события, а  функция плотности распределения моментальной мощности в каждой своей точке имеет самоподобную природу. 

( Читать дальше )

     В задачах оценки бизнес проектов, прогнозирования спроса, определения справедливой цены опциона или портфельного инвестирования, так или иначе, возникает проблема адекватной оценки рисков.  Обычно за риск принимается простое, выборочное среднеквадратичное отклонение, для которого хорошо разработан аппарат математической статистики, позволяющий прогнозировать критические показатели, например просадки,  и проводить стресс-тесты в предположении центральной предельной теоремы, то есть в предположении узкой стационарности  наблюдаемых процессов.

     Однако, мы зачастую имеем дело с абсолютно  другими, нестационарными процессами. Не стационарность процесса может быть вызвана  как нелинейным синергетическим эффектом  (реклама и «сарафанное радио»,  мода, политические выборы, революции и пр. самоорганизации),  как множественностью состояний системы (тренд/флэт), так и просто  некоторой инерцией системы, связанной, например, с задержкой принятия решений основными игроками.

( Читать дальше )