Блог им. Kot_Begemot |Ухмылка неопределенности для трендовых стратегий
- 25 сентября 2021, 10:49
- |
Сегодня все будет просто — мы будем строить идеальную торговую систему. При этом наша система будет трендовой, с характерным временем удержания позиции или, иначе говоря, горизонтом прогноза.
Сейчас мы ещё не научились ничего предсказывать, и не знаем ничего о том что там происходит на рынках — работают там тренды, контр.тренды, или фундаментальный анализ. Поэтому заменим наше настоящее незнание идеальной моделью, заглядывающей в будущее на определенный горизонт и, соответственно, обладающей идеальной предсказательной силой.
Дадим нашей модели 5 лет истории золота, таймфрейма м15 и попросим ее показать нам мастер класс:

Рис 1. Базовый актив (Золото) и результаты сверх идеальных ценовых торговых систем в зависимости от времени удержания позиции, учитывая издержки
Видно, что даже сверх идеальная модель теряет предсказательную силу с ростом горизонта прогноза приблизительно пропорционально корню из времени. К тому же, в этом модельном эксперименте мы все таки немного смухлевали, предположив, что наша идеальная модель видит априорно неточное будущее идеально точно. На самом деле, если будущее туманно, то и его ясновидение может быть исключительно туманным. А когда одна неопределенность (видение) описывает другую неопределенность (будущее), как известно, возникает улыбка неопределенности)))
( Читать дальше )
- комментировать
- ★1
- Комментарии ( 11 )
Блог им. Kot_Begemot |Критическая масса и критическое значение - большой эмпирический тест
- 29 мая 2021, 11:15
- |
Ранее, и в ходе дискуссий, мы получили три статистических оценки для качества аппроксимации данных длинной L (коэффициент Шарпа) со стороны случайных наборов коррелированных признаков (Features) размерностью N и корреляционной матрицей C.
Для случайного признака :
Для лучшего признака из набора :
( Читать дальше )
Блог им. Kot_Begemot |Критическая масса и критическое значение аналогичных стратегий
- 26 мая 2021, 04:03
- |
В первой части мы анализировали критический порог статистической значимости для сложных композитных систем на примере модели AR. В этот раз мы попытаемся быть чуть ближе к делу и проведем тесты для набора трендовых систем на базе Simple Moving Average. В качестве примера возьмем самый ликвидный фьючерс — белый шум, для которого заранее известно, что он абсолютно «не торгуемый» и попытаемся всё же что-нибудь под него подобрать из соображений трендовости «больших денег» и саморефлексии участников торгов.
Сгенерируем набор из 10 стратегий с периодом 10*i, i=1,2,...10.
Nstr=10;
x=randn(10000,1);
y=[x(2:end);0];
M=zeros(10000,Nstr);
for i=1:Nstr;
M(:,i)=tsmovavg(x,'s',10*i,1);
end;
M(1:Nstr*10,:)=0; R=M.*y; И оценим порог 70% статистической значимости коэффициента шарпа стратегии без учета размерности набора стратегий:
( Читать дальше )
Блог им. Kot_Begemot |Критическая масса и критическое значение
- 24 мая 2021, 00:23
- |
Проведем небольшой тест — возьмем один случайный фьючерс, приращения которого представлены временным рядом случайных чисел, и набор случайных стратегий, представленный множеством N временных рядов случайных чисел (он же матрица признаков, фичей, пространство предикторов и т.д.) и попытаемся найти из этого большого набора тот признак, который будет лучше всего говорить нам когда покупать фьючерс, а когда продавать. Что это будет, мультипликатор P/E, фаза луны или MACD — не важно, главное чтобы на выходе получилась «идея» или, как ещё говорят, «грааль».
Хорошо известно, что случайная стратегия примененная к случайному инструменту даст случайное эквити, которое будет иметь гауссову плотность распределения коэффициента шарпа с математическим ожиданием 0 и среднеквадратичным отклонением
где L — число известных значений случайного фьючерса.
Это означает, что достаточно большое множество случайных стратегий (или случайных признаков), примененных к случайному фьючерсу абсолютно случайным образом окажутся способными достаточно хорошо описать любое поведение случайного фьючерса (отклика) в бек-, форвард-, голкипер-, кросс-, спринт- и всех прочих тестах… но только на истории.
( Читать дальше )
Блог им. Kot_Begemot |Обобщённый подход к диверсификации рисков
- 28 августа 2019, 04:47
- |
- Обобщённая проблема
Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.
Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:
где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.
( Читать дальше )
Блог им. Kot_Begemot |Портфельная оптимизация как бустинг на «слабых» моделях-3
- 21 августа 2019, 13:49
- |
Устойчивые долгосрочные модели
В предыдущих частях (часть 1, часть 2) мы рассмотрели построение композитных систем оценок ценных бумаг, построенных при помощи распространённых средств машинного обучения (Bag/Boost методы). Однако, такой подход, несмотря на все свои преимущества (скорость, точность) имеет ряд больших недостатков – отсутствие универсальности моделей в результате проблем «переобучения» (точной настройки на определённые типы рынков и временные интервалы) и сложность интерпретации полученных композиций.
В результате решения этих проблем мы разработали базовую модель на основе наших представлений о стохастических дифференциальных уравнениях с квантовыми скачками, образующих улыбку волатильности. Эта макромодель получила в наших исследованиях наиболее полную микроскопическую интерпретацию.
( Читать дальше )
Блог им. Kot_Begemot |Тестирование стратегий - Walk Forward Test vs CV Fold Test
- 02 мая 2019, 00:22
- |
В классических задачах прогнозирования используются в основном различные Fold тесты. Их логика весьма понятна и прозрачна – защитить алгоритм от переобучения и получить лучшие стационарные параметры регуляризации. Например, такие, как лямбда Тихонова, или, если речь идёт о бустинге на деревьях решений – минимальное количество листьев. Однако сообщество Smart Lab настоятельно рекомендовало нам провести Walk Forward тесты, логика которых нам мало понятна.
А если логика не понятна, то можно детально рассмотреть какой-нибудь простой пример.
Пусть в качестве объекта прогнозирования у нас будет выступать простая синусоида с частотой ω и амплитудой А. Без применения сложных математических методов эта задача решается следующим образом:
- Берутся исторические данные
- На основе данных подбираются параметры амплитуды, частоты и фазы.
- Исходя из полученных «динамических» переменных модели строится прогноз на будущее.
( Читать дальше )
Блог им. Kot_Begemot |Портфельная оптимизация как бустинг на «слабых» моделях
- 29 апреля 2019, 22:09
- |
Часть 2.
В прошлой части мы подбирали такую комбинацию статистических оценок динамики акций, которая давала нам возможность стабильно выбирать портфель акций лучше среднерыночного, с показателем Шарпа на 26% выше индексного.
Мы также пробовали составлять портфель из портфелей и портфель на основе портфеля оценок, но в силу высокой линейной зависимости оценок и полученных на них портфелей друг от друга Bagging ожидаемо не дал никакого результата.
Тем не менее, этот важный этап подготовительных работ – построение портфеля (или композиции портфелей) на простых, статистических оценках дал нам некоторую отправную точку, относительно которой мы будем рассматривать эффективность всех наших последующих нововведений.
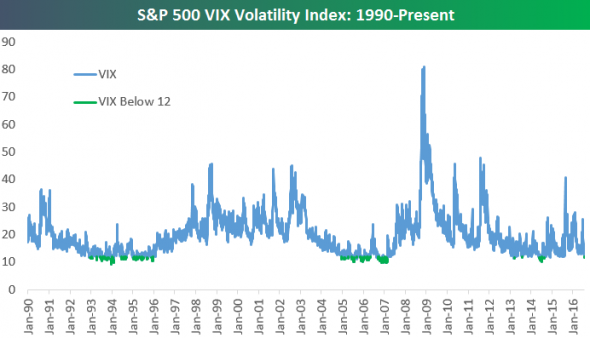
Рис. 6. Иллюстрация динамики волатильности акций США, входящих в состав индекса S&P 500.
Основную проблему стандартных методов мы видим в том, что они разработаны для стационарных стохастических процессов, в то время как любые финансовые (а зачастую природные, биологические и др.), временные ряды имеют нестационарную природу. Так, например, широко известно, что логарифмическое изменение стоимости акций является нестационарным процессом со склонностью к консолидации (кластеризации) волатильности.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс