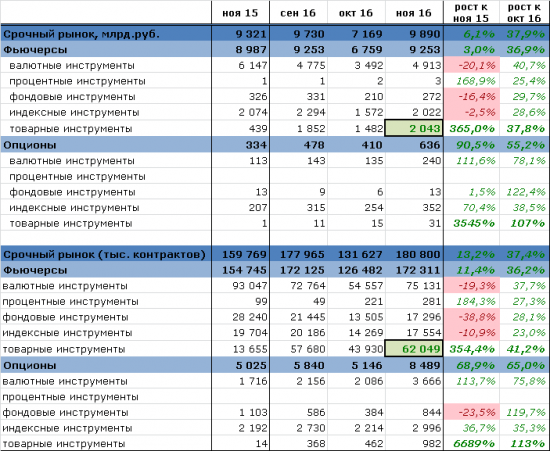
ПОВЫШЕНИЕ ТАРИФОВ НА СРОЧНОМ РЫНКЕ НИКАК НЕ ОТРАЗИЛОСЬ НА ОБЪЁМЕ ТОРГОВ!!!

Против падения на 25% в октябре, в ноябре рост +38%!!!

И как бы не плакали, стонали, голодали алготрейдеры — видимо всё это с жиру —  на повышение тарифов они ответили перевыполнением стохановских норм и продолжили жрать кактус профит.

Гудбай Ri, Да здравствует Brent!

В ноябре 2016 произошло знаменательное событие, объем торгов по товарным инструментам обогнал объемы торгов по индексным инструментам. 

Так же поставлен рекорд по объему торгов опционами!

( Читать дальше )

Тимофей Мартынов - 

Приз «Лучшая инновационная идея в инвестициях» 300 тыс. рублей получена будущими «убийцами смартлаба» —  Conomy. Ну если бы у меня были 30 сотрудников, то возможно у меня бы еще были шансы на выживание, а так конечно шансов нет.  Парни взяли приз за инвестиционного робоадвайзера, который учитывает риск-профиль клиента. Думаю, справедливая награда. Действительно что-то свеженькое, инновационное.

"Я честно говоря ваще не верю в суть робоадвайзинга"

( Читать дальше )

Вспомогательная разметка линейными трендами дней и часов



( Читать дальше )

здесь была Хроника

А сейчас первые Итоги Голодовки по основной сессии.




Первый блин конечно комом, т.к. голодовка совпала с невероятной волатильностью и объёмом торгов по нефти, и не все АлгоТрейдеры удержались от работы, Но!

Но при росте дневных объёмов торгов по нефти на 56,7% объём торгов по Si снизился на 10%. А значит АлгоТрейдеры показали относительно впечатляющий результат протеcтного движения.

Хотя по личным субъективным ощущениям ничего не поменялось.

Ri провёл сессию стабильно чуть выше среднедневных значений. 

Падение реально наблюдалось в GZZ(-19,1%)и MMZ(-35,0%) но они и так малоликвидны и на общую картину результатов забастовки не влияют


( Читать дальше )

Хроника Всероссийских «Голодных игр» АлгоТрейдеров в знак протеста против повышения тарифов.

19:00 День Голодовки АлгоТрейдеров | Итоги


7 часов — Ещё час простоять, да 45мин продержаться

SIZ6 - -7%! Голодают только самые стойкие мальчиши-алгочиши, остальные уже пилят...
RIZ6 - +14%!
BRZ6  —  +77%! Идём на рекорды!

6 часов — жадность по всем фронтам

SIZ6  — -7%! 
RIZ6  — +15%!
BRZ6  —  +65%!

15:00 — 5 часов противостояния жадности, гордости и ко'рысти

SIZ6  — Падение объёмов резко сократилось до  -14% Жадность побеждает (или корысть, или пох… изм). 

( Читать дальше )

Фэншуйный Свежий Нелинейный индикатор Сегодняшнего Дня

Не даёт отвлекаться от торговли и быть в Тренде СмартЛаба.

Ссылка — UL.lua
Копируем, устанавливаем, запускаем на каждом графике.




( Читать дальше )

Давно наблюдаю устойчивую корреляцию между EUR/USD — GOLD на уровне 0.7-0.8 (по Пирсону)


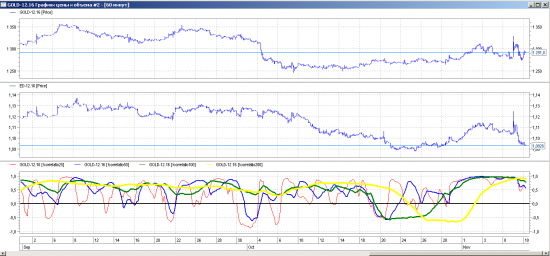
Больше как вопрос к сообществу: Кто нибудь рассматривал/торговал данную пару? насколько успешно? и есть ли смысл заниматься?

Языком сухих цифр

1. Тарифы увеличены в 1,5-2 раза. (с октября) — «бедные» HFT- трейдеры стонут: "Прибыли падают, работать не дают! ЗАБАСТОВКА! ГОЛОДОВКА!"

2. Выплаты Московской Биржи маркетмейкерам за 9 месяцев 2016 года выросли на 109,5млн.руб. (+46,5%) (344,5 млн.руб. за 9 месяцев)
- «бедные» HFT- трейдеры многозначительно молчат.

 (Консолидированная промежуточная сокращенная финансовая отчетность за первые 9 месяцев 2016 года по МСФО (англ.) страница 14, Market makers fees)

Господа HFT, ведь явно рост выплат будет продолжен в связи с изменением тарифов???

Не поделитесь на сколько???

Молчим???

Упрощенный алгоритм вычисления приближенного значения размерности Минковского, для ценового ряда.

Краткая справка:

Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:

• где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.

Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов. 

( Читать дальше )

ЗАВТРА В БОЙ!!!

А многие молодые квикеры-бойцы до сих пор пользуются стандартными индикаторами, машками, болинджерами и параболиками, а некоторые и вообще ничем не пользуются.

И в глазах опытных «охотников» за депозитами:



экипировка молодого бойца выглядят так:


( Читать дальше )