Блог им. uralpro |Торговая система с возвратом к среднему
- 25 июня 2017, 18:48
- |
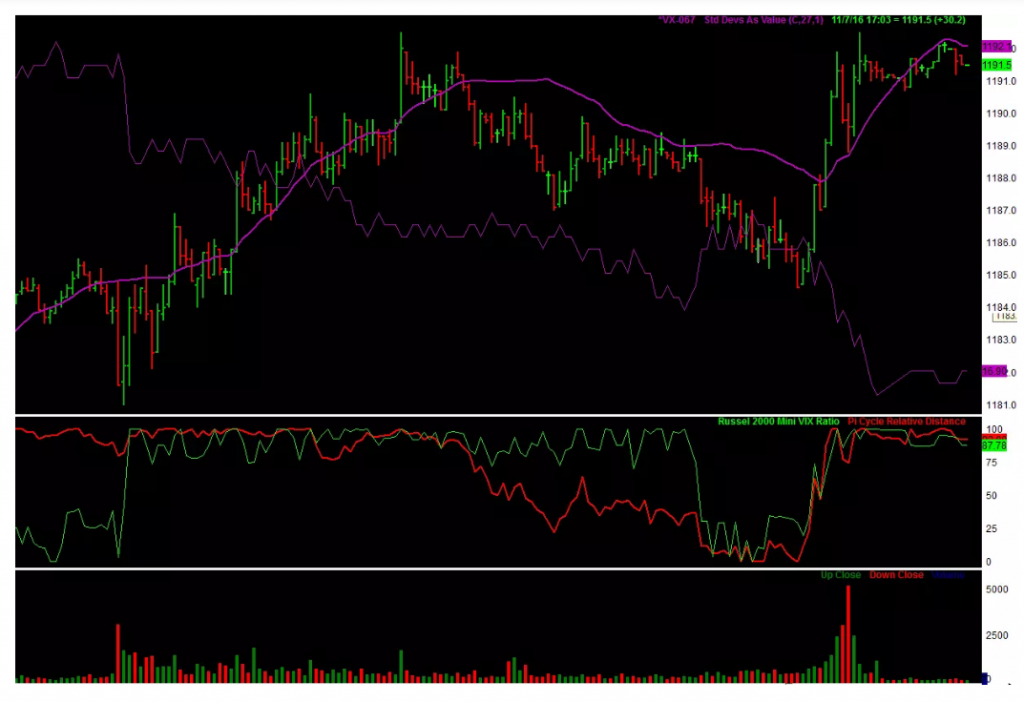
Статья с сайта www.miltonfmr.com, из которой можно взять некоторые приемы, пригодные даже для использования в высокочастотной торговле.
Многие трейдеры, создающие и правильно применяющие торговые системы с возвратом к среднему, получают хорошую прибыль. Факты говорят о том, что рынки двигаются в соответствии с паттернами, одним из которых является цикличность. Простыми словами, все, что двигалось вверх, должно пойти вниз и наоборот. Ничто не движется в одном направлении вечно. Применительно к рынкам, у нас есть два возможных исхода — тренд, либо определенный торговый диапазон с возвратом к среднему. В прошлых наших исследованиях было показано, что гэп на открытии определяет тренд на остаток дня в 30% случаев. Это значит что из 20 торговых дней мы имеем 6 трендовых дней без возврата к среднему. С другой стороны у нас есть 70% движения цены, которая имеет тенденцию к возврату к среднему значению несколько раз за день. Важно отметить, что эти 70% относятся к внутридневному движению цен.
( Читать дальше )
- комментировать
- ★40
- Комментарии ( 10 )
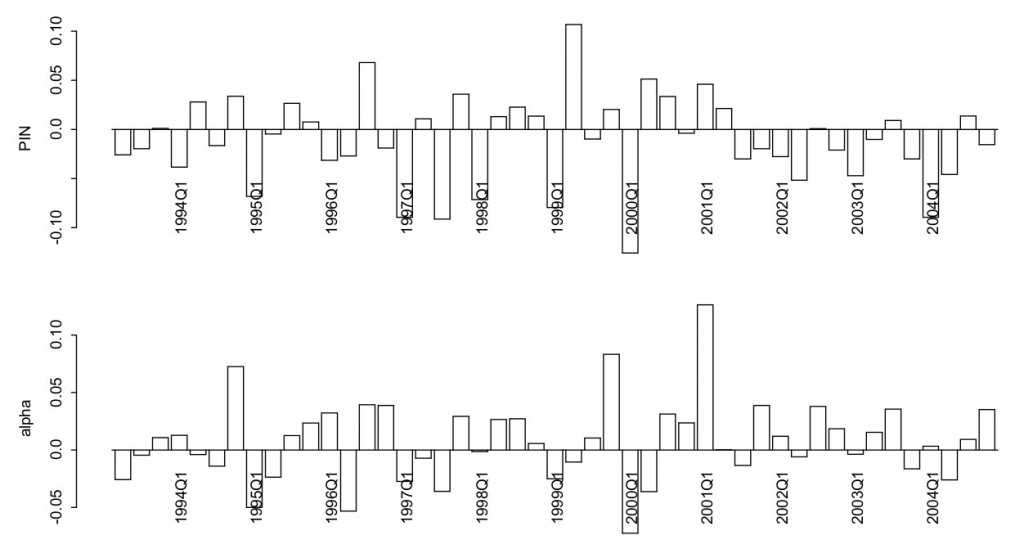
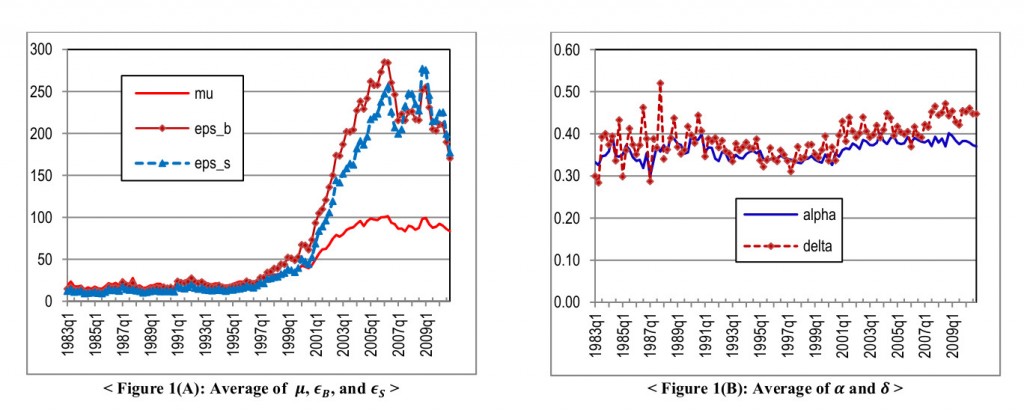
Блог им. uralpro |Измерение информации на рынке с помощью PIN. Часть 3
- 11 июня 2015, 11:38
- |
Окончание. Начало см. в блоге и на моем сайте.
В этой, последней части цикла разберем пример вычисления PIN с применением языка R. Кроме библиотеки PIN языка R будем использовать также библиотеку highfrequency.
Для примера автор берет сгенерированные данные, которые соответствуют формату TAQ — стандарт для акций NYSE. Данные состоят из двух наборов — временной ряд ценового котирования (sample_qdata) и сделки (sample_tdata) и предоставляются в открытом доступе вместе с библиотекой highfrequency.
Нужно отметить что используемые данные взяты только за один торговый день. Обычно, для вычисления PIN применяют больший набор данных, не менее, чем за 60 дней, чтобы выборка была достаточной для правильного определения параметров. Наши данные нужны только для демонстрации процесса получения PIN. Библиотека PIN позволяет это сделать для выборки с любой размерностью, что позволяет применять ее и для высокочастотной торговли. Пример, приводимый здесь, может быть легко расширен для вычисления на другом временном горизонте, большим, чем один торговый день.
( Читать дальше )
Блог им. uralpro |Измерение информации на рынке с помощью PIN. Часть 2
- 09 июня 2015, 12:48
- |
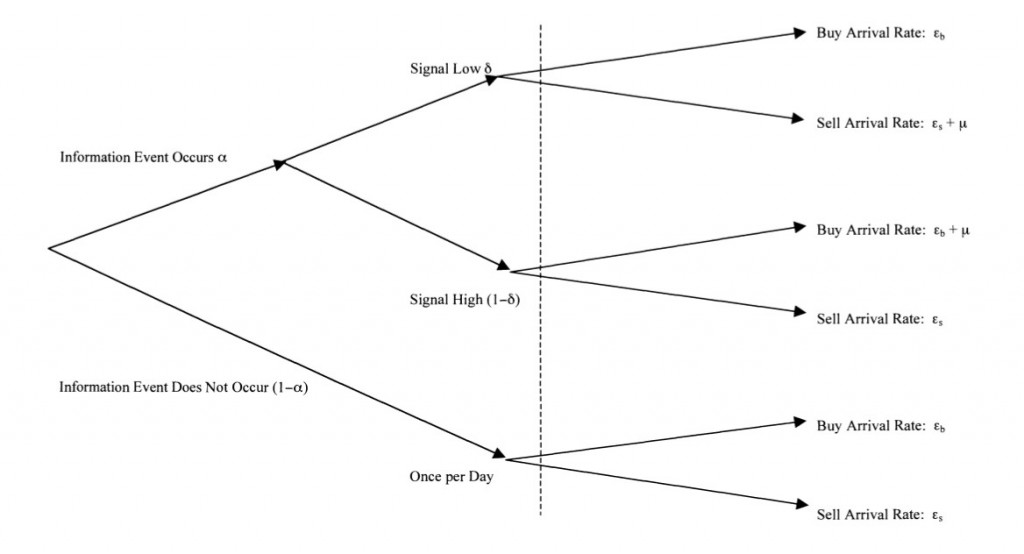
В прошлой части мы рассмотрели теоретическую модель, лежащую в основе вычисления вероятности присутствия на рынке информированных трейдеров PIN. Продолжим с эмпирической реализации этой модели.
Для уменьшения пространства параметров модели, обычно предполагают, что частоты прихода ордеров на продажу ϵs и на покупку ϵb равны. В день «хорошей новости» вероятность наблюдения последовательности сделок купли и продажи соответствует:
![Измерение информации на рынке с помощью PIN. Часть 2 \exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^B}{B!}\exp(\epsilon T)\frac{(\epsilon T)^S}{S!}](http://mathurl.com/q2uamv5.png) , где B и S — число сделок купли и продажи соответственно.
, где B и S — число сделок купли и продажи соответственно.
( Читать дальше )
Блог им. uralpro |Измерение информации на рынке с помощью PIN. Часть 1
- 04 июня 2015, 12:47
- |
В нескольких статьях мы рассмотрим использование индикатора PIN, который представляет собой вероятность присутствия на рынке так называемых информированных трейдеров. Статьи основаны на работе Paolo Zagaglia "PIN: Measuring Asymmetric Information in Financial Markets with R". Так как вероятность информированной торговли зависит от сделок купли и продажи в течение рабочего дня, в данном цикле мы рассмотрим весь процесс, от обработки исходных данных и вычисления вероятности информированной торговли, до определения параметров лежащей в основе математической модели. Примеры будут сопровождаться кодом на языке R.
Рост в последние годы алгоритмической и высокочастотной торговли открыл тот факт, что динамика биржевых цен сильно зависит от микроструктуры рынка. В частности, некоторые трейдеры могут иметь доступ к приватной информации о торгах, в то время как другие довольствуются только публичными новостями. Риск того, то неинформированный трейдер может в какой-то момент времени столкнуться в качестве контрагента в сделке с информированным, является одним из параметров, определяющих цену актива. Таким образом, измерение вероятности того, что контрагент владеет ассиметричной информацией, позволяет правильно вычислить цену.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс