Блог им. uralpro |Измерение токсичности потока ордеров. VPIN для HFT. Часть 2
- 08 июля 2015, 11:28
- |
Прошлая часть — в моем блоге.
Стандартный подход к вычислению PIN состоит в нахождении методом максимального правдоподобия ненаблюдаемых параметров (α,δ,μ,ϵ) описывающих стохастический процесс трейдов, и последующем вычислением PIN из этих параметров. Мы представим аналитическую оценку токсичности, не требующую промежуточного вычисления ненаблюдаемых величин. Мы обновляем нашу метрику в привязке к объемам для учета скорости прибытия новой информации на рынок. Эта метрика, которая называется VPIN, предоставляет простую оценку токсичности потока ордеров в высокочастотном окружении.
Природа информации и времени
Информация в модели последовательной торговли в общем виде представляет из себя данные, которые несут сообщение о будущем уровне цены актива. На эффективном рынке, значение цены актива отражает его полную информационную величину, в связи с тем, что информированный трейдер стремится получить прибыль от владения этой информацией. Так как маркет-мейкер может занимать как длинную, так и короткую позиции, будущие движения актива влияют на его прибыльность, и он пытается извлечь информацию из паттернов торговли. Эти его попытки отражаются в устанавливаемых уровнях бида и аска.
( Читать дальше )
- комментировать
- ★12
- Комментарии ( 11 )
Блог им. uralpro |Измерение токсичности потока ордеров. VPIN для HFT. Часть 1
- 07 июля 2015, 14:20
- |
В статьях об индикаторе PIN мы определили, что на рынке присутствуют два типа трейдеров — информированные и неинформированные. Заявки неинформированных трейдеров всегда подвержены adverse selection risk со стороны информированных. Ситуация, когда после исполнения таких заявок цена движется в невыгодную для неинформированных участников сторону, называется токсичностью потока ордеров. Индикатор PIN служил для измерения этой токсичности, в данной статье мы рассмотрим усовершенствованный индикатор VPIN, который применим и для высокочастотной торговли. Цикл статей основан на публикации Maureen O’Hara "Flow Toxicity and Liquidity in a High Frequency World". Будет все описываться очень подробно, потому что, кроме нахождения непосредственно VPIN, в этой публикации много интересных выводов и фактов.
( Читать дальше )
Блог им. uralpro |Исправления в "Алгоритмах маркетмейкера"
- 18 июня 2015, 13:48
- |
В цикле статей "Алгоритмы маркетмейкера" в пятой части был размещен мой код на C# для реализации стратегии оптимального управления ордерами. Пользователь сайта Eskalibur обнаружил в нем несколько ошибок, которые значительно влияли на результат, и доработал алгоритм до полного соответствия оригинальной статье. Его код я поместил в конце пятой части цикла статей (см. также комментарии к ней). Прошу всех, кто пробует применять эту стратегию, использовать именно этот листинг.
Хочу выразить благодарность за проделанную работы Eskaliburу и пользователю r0man, который также работает в направлении практического применения алгоритма. Думаю, у них все обязательно получится, и по результатам разместим отдельную статью на сайте.
Блог им. uralpro |Стратегия с классификацией ордеров по времени жизни. Часть 2
- 26 мая 2015, 13:43
- |
В прошлой части нами было сделано наблюдение, что для присутствующих на рынке высокочастотных алгоритмов характерна высокая частота отмены биржевых ордеров. В данной статье мы уделим внимание еще одной особенности HFT роботов — малому объему ордеров, генерирумых подобными стратегиями.
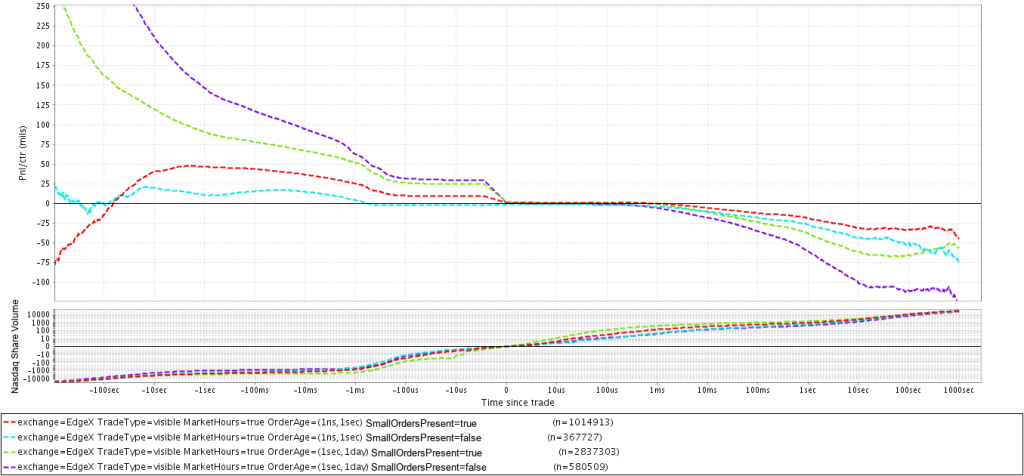
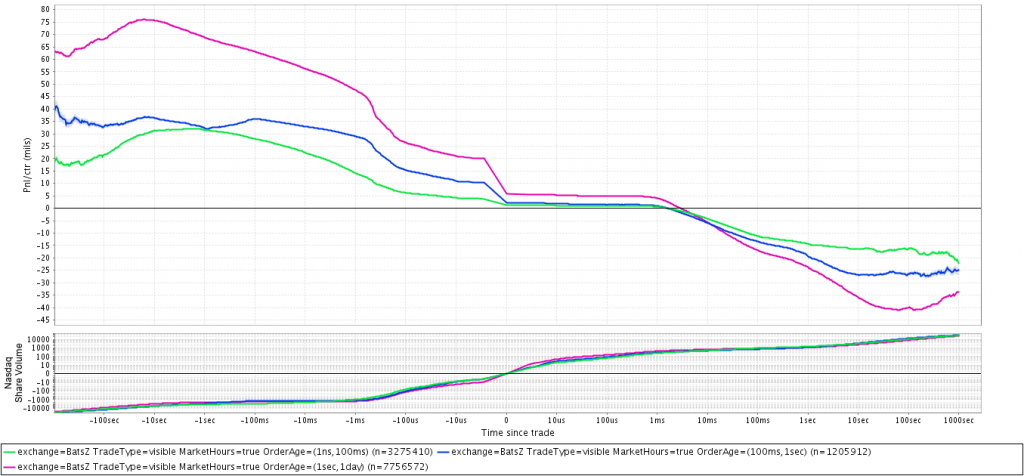
Автоматические стратегии стараются отсылать биржевые приказы, которые содержат небольшие количества акций или лотов. Маркет мейкеры делают это для того, чтобы выборочно торговать с небольшими контрагентами, обходя сильные движения, вызываемые крупными покупками или продажами. Исполнительные алгоритмы отсылают небольшие ордера, чтобы скрыть свои намерения о реализации крупных объемов, избегая тем самым сильного воздействия на цену. Чтобы проверить, действительно ли существуют описанные тенденции на рынке, построим график движения цены, с точки зрения пассивной стороны трейда, после взятия всех ордеров на конкретном уровне для двух ситуаций — когда малые ордера принимают участие в данном трейде, и когда их нет. За малый объем ордера примем 2 целых лота и менее:
( Читать дальше )
Блог им. uralpro |Стратегия с классификацией ордеров по времени жизни. Часть 1
- 22 мая 2015, 13:52
- |
Неплохую идею для высокочастотного трейдинга подсказал Kipp Rogers в своем блоге. Идея несложная, но требующая подробного объяснения, поэтому попробую изложить ее в двух статьях.
Автор предположил, что лучшее исполнение ордеров, отправленных на биржу, скорее возможно получить, торгуя с трейдерами — людьми, вручную отправляющими приказы, чем с компьютерами, то есть контрагентами с автоматическим выставлением. Высокочастотные роботы отправляют приказы на биржу только в том случае, если они видят возможность быстрого снятия прибыли или ищут наилучшую цену исполнения для больших объемов, что делает соревнование с ними очень тяжелой задачей. С другой стороны, трейдеры, торгующие вручную ( под ними могут подразумеваться и автоматические программы с медленными алгоритмами ), выставляют приказы с большим временем жизни (до отмены или исполнения), меньше внимания уделяют мгновенной цене и, как правило, имеют идею о направлении движения цены при входе в рынок, что также дает представление о поведении их ордеров.
( Читать дальше )
Блог им. uralpro |Алгоритмы маркетмейкера. Часть 5
- 09 апреля 2015, 11:27
- |
Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора 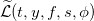 , в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью
, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью 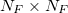 , где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
, где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
( Читать дальше )
Блог им. uralpro |Алгоритмы маркетмейкера. Часть 4
- 07 апреля 2015, 11:25
- |

Прошлые части цикла здесь. В этой части статьи мы найдем численное решение системы уравнений оптимального управления позицией маркетмейкера. Такое решение легко запрограммировать и использовать в реальной торговле для контроля за лимитными и маркет ордерами в соответствии с полученными стратегиями θmk,θtk. Для упрощения разложим функцию владения на слагаемые, чтобы получить сокращенную функцию владения v(t,y,f,s), которая представляет собой только динамическую составляющую основной функции:
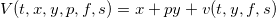
( Читать дальше )
Блог им. uralpro |Алгоритмы маркетмейкера. Часть 3
- 02 апреля 2015, 09:46
- |
Продолжаем разбирать работу JIANGMIN XU «Optimal Strategies of High Frequency Traders». Чтобы составить уравнение оптимального контроля, сначала сформулируем проблему оптимизации алгоритма при используемых стратегиях θ, как достижение максимума следующего матожидания:
![Алгоритмы маркетмейкера. Часть 3 \max_{\theta^{mk},\theta^{tk}}\mathbb{E}_0[X_T-\gamma\int^T_0 Y^2_{t-}d[P,P]_t]](http://mathurl.com/pthr6jr.png) ,
,
( Читать дальше )
Блог им. uralpro |Алгоритмы маркетмейкера. Часть 2
- 31 марта 2015, 11:10
- |
В прошлой части мы рассмотрели оптимальное управление inventory risk в маркетмейкерском алгоритме. Напомню, что формулы для нейтральной цены и оптимального спреда между лимитными ордерами были получены при допущении, что цена следует геометрическому броуновскому движению. Управление inventory risk для моделей цены, более приближенными к реальности, рассматривается, например, в статье Pietro Fodra & Mauricio Labadie «High-frequency market-making with inventory constraints and directional bets» . Однако, применить напрямую на практике алгоритмы из этих статей вряд ли получится, так как в них не учитывается действие adverse selection risk. Поэтому в данной части рассмотрим работу JIANGMIN XU «Optimal Strategies of High Frequency Traders», в которой автор делает попытку учесть этот вид риска, конечно, наряду с inventory risk.
( Читать дальше )
Блог им. uralpro |Алгоритмы маркетмейкера. Часть 1
- 26 марта 2015, 11:26
- |

В биржевой торговле существует ряд алгоритмов, которые можно отнести к маркетмейкерским. Как правило, это означает выставление лимитных ордеров по обе стороны стакана, то есть как на покупку, так и на продажу, и целью такого алгоритма является получение прибыли от спреда - разницы между этими лимитными ордерами. Простейшая стратегия подобного рода — постановка ордеров одновременно на лучший бид и лучший аск — будет убыточной из-за действия следующих факторов:
1. Вероятность взятия ордера на стороне, противоположной движению цены в большинстве случаев выше, чем на стороне по направлению движения. То есть, если цена актива растет, то чаще будут исполняться ордера, выставленные на продажу, а ордера на покупку, соответственно — реже, в результате возникает убыточная позиция. В англоязычной литературе этот эффект называется
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс