Избранное трейдера Burzhui
Синтез торгового алгоритма методом генетического программирования
- 29 января 2016, 19:39
- |
Метод ГП по своим свойствам потенциально мог бы являться универсальным методом поиска алгоритма оптимизирующего заданную целевую функцию. И я как любитель эволюционной оптимизации не мог пройти мимо такой заманчивой идеи.
Торговый алгоритм ищу в виде набора элементарных функционалов. Каждый функционал может иметь любое количество входов и по крайней мере один выход. Вход и выход характеризуется типом данных. Выход одного функционала может быть подан на вход другого при условии, что тип данных входа и выхода совпадает.
Например, функционал вычисления минимума/максимума в заданном окне получает на вход интересующую величину и значение размера окна, а также имеет 4 выхода: минимум/максимум, позиция точки минимума/максимума в окне.
ГП должен подобрать функционалы и связать их входы и выходы так, чтобы в итоге получился единственный выход типа сигнал (сигнал есть либо нет), который и будет являться сигналом на покупку/продажу. Связанные функционалы с общем случае образуют граф. Целевой функцией является критерий Шарпа с поправкой — наказанием за информационную сложность алгоритма.
( Читать дальше )
- комментировать
- ★11
- Комментарии ( 14 )
Препарируем процесс торговли с помощью простейшего тервера
- 13 декабря 2015, 16:49
- |
Сейчас я попробую разложить торговлю по полочкам, вычленить независимые составляющие и их проанализировать.
Пусть у нас есть торговый алгоритм, который выдает приказ на покупку или продажу. Для выхода используем тупой алгоритм типа таймаут, случайный выход, выхода по стоп-лосс, тейк-профит, трейлинг-стоп и т.п. Комиссию не учитываем.
Обозначим рекомендацию алгоритма O[i] = -1, 0, 1, где i — номер потенциальной сделки. -1 соответствует рекомендации продать, 1 — купить, 0 — ничего не делать. Объем сделки обозначим V[i] >= 0.
Результат сделки и при единичном объеме и при условии что только покупаем обозначим R[i]. Будем считать что на рынке на всем периоде торговли нет устойчивого тренда вверх т.е. стратегия “купил и держи” в среднем прибыли/убытка не приносит. Тогда матожидание (M) от произвольной сделки на покупку равно нулю M(R[i])=0.
Итого, мы разделили торговлю на три независимые составляющие:
( Читать дальше )
Получение внутридневных данных c IQFeed
- 13 августа 2015, 08:59
- |
Статья о загрузке внутридневных котировок от поставщика данных IQFeed на языке Python опубликована в блоге www.quantstart.com. DTN IQFeed — популярный вендор, поставляющий данные со многих американских и европейских рынков по широкому спектру инструментов. Тем трейдерам, кто практикует алгоритмическую торговлю на зарубежных площадках или использует данные с них для поиска корреляций с российскими активами, будет очень полезен нижеследующий перевод.
С IQFeed возможно получение данных через сокет соединение к локальному серверу IQLink, который предоставляется при создании аккаунта у этого поставщика данных. В этой статье мы будем использовать потоковое сокет соединение на языке программирования Python для буферизации данных и создадим файл CSV с внутридневной маркет датой для американских акций.
( Читать дальше )
Разметка минимумов и максимумов по Ларри Вильямсу: пример на USD/RUB
- 02 августа 2015, 00:45
- |
Для начала все же загляните в пост по ссылке и увидите там два паттерна, максимум и минимум. Определяются они очень просто:
- локальный максимум, это бар который имет два соседних с максимумами ниже
- локальный минимум, это бар который имет два соседних с минимумами выше
В этом случае получается:
- краткосрочный максимум, это локальный максимум который имеет два соседних ниже
- краткосрочный минимум, это локальный минимум который имеет два соседних выше
( Читать дальше )
Все паттерны Ларри Вильямса в одной картинке
- 01 августа 2015, 15:27
- |

Пользуйтесь на здоровье!
P.S.
Если где-то есть явная ошибка ввиду неверной интерпретации (есть сомнения насчет прорыв вверх/вниз) — комментируем.
UPD.
продолжение: развернуто про минимумы и максимумы по Ларри Вильямсу...
Еще одно тестирование алгоритма Маркет Мэйкера
- 10 июля 2015, 09:42
- |
Продолжая тему тестирования алгоритма Маркет Мэйкера, поделюсь своими результатами и мыслями по его работе:
1. Основной режим работы алгоритма — это маркетмэйкинг (он же арбитраж ликвидности, он же торговля спредом). И конечно же, прибыльность этой стратегии сильно зависит от рыночных условий, скорости получения данных и работы системы исполнения. Средняя прибыль на сделку даже и при идеальном исполнении не будет превышать значение спреда (2-5 пунктов по Si в среднем). А в период сильной волатильности, когда стакан бросает из стороны в сторону на 10-30 пунктов, несмотря на большое количество положительных сделок ( около 70%), алгоритм становится убыточным. В основном из-за комиссий, конечно.
2. Да, математические формулы сильно ограничили многих желание понять, как устроен алгоритм. Но на самом деле, если вдумчиво посмотреть картинки (карты политик), получается все ясно и просто. А будет еще проще, если посмотреть картинки графиков из других статей, лежащих в основе алгоритма (например Guilbaud, Fabien, and Huyen Pham, 2013, Optimal high-frequency trading with limit and market orders). Забудем на минутку про дисбаланс бид/акс объемов и построим карту политик для открытой позиции при разных значениях спреда:
( Читать дальше )
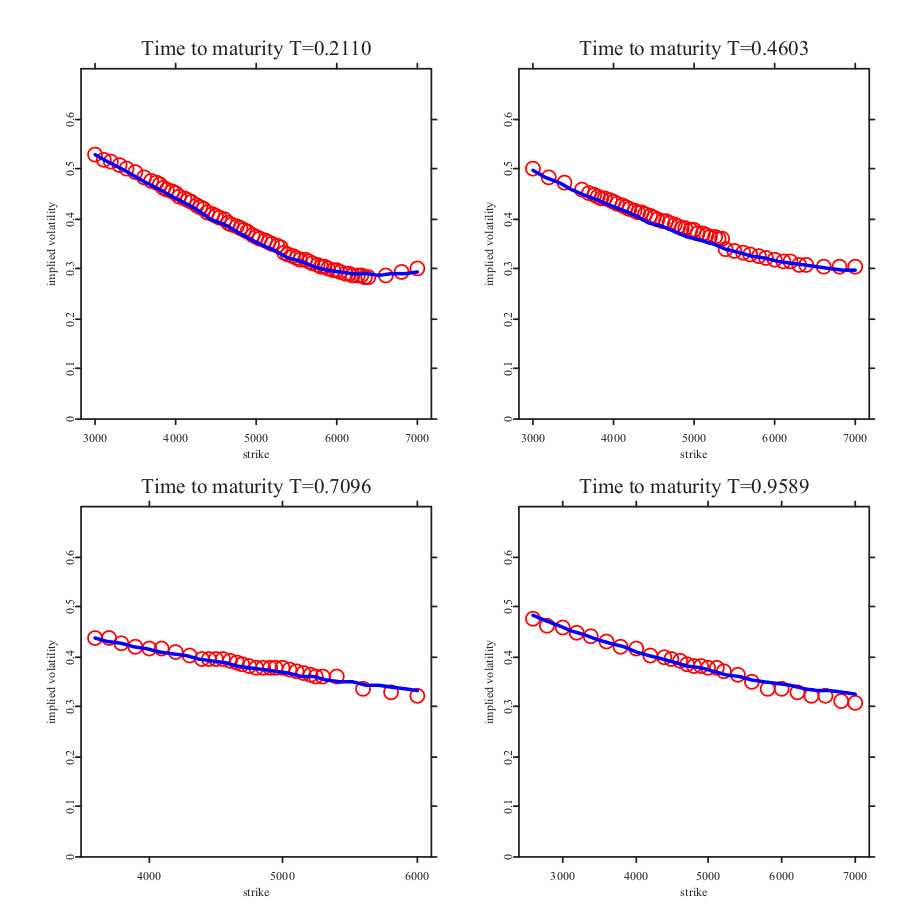
Улыбка волатильности. Модель Бейтса
- 07 мая 2015, 10:15
- |
Продолжение. Начало в моем блоге и на сайте.
В прошлой статье про модель Хестона мы отметили, что она обладет недостатком, который проявляется в неточности определения цен опционов на малых сроках экспирации. Здесь мы рассмотрим модель Бейтса, в которой этот недостаток устранен, и она является одной из лучших аппроксимаций, описывающих поведение цен опционов для разных страйков и периодов до экспирации.
Модель Бейтса относится к моделям стохастической волатильности и определятся следующими уравнениями:
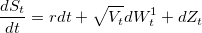
( Читать дальше )
Где обучаться алготрейдингу?
- 22 марта 2015, 18:11
- |
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал