Делаю новую алгоритмическую торговую систему (АТС) под Quik. Базовой в системе является достаточно сложная многопоточная C++ DLL, связывающаяся с Quik через Lua. Для разработки с самого начала использовалась VS 2015. Т.к. в настоящее время перешел на х64 Quik занялся перекомпиляций всего своего х86 софта под Quik на платформу х64.
Все бы ничего, но при больших рыночных потоках данных Quik начинал подтормаживать, а при подключении DDL, Quik подтормаживал еще сильнее и через некоторое время падал вместе с DLL. Переход на х64 существенно улучшил ситуацию, Однако эпизодические падения, значительно реже, но продолжались.
Надо сказать, что все эти многопоточности и были ранее введены в DLL для снижения нагрузки на Quik, чтобы не грузить поток событий терминала. Вся обработка событий заключалась лишь в том, чтобы преобразовать данные получаемые из Lua и отдать их соответствующему потоку для дальнейшей обработки.
В общем, о стабильной АТС приходилось только мечтать, и думать что дальше с этим делать.
У меня на компе давно без дела пылилась Visual Studio 2017. Требований к железу она предъявляет больше чем VS 2015, и я ее использовал считанные разы, скорее, чтобы посмотреть что в ней нового и отличия от VS 2015. Существенных отличий не заметил, и продолжал работать на старой VS 2015.

( Читать дальше )

Не далее как вчера опубликовал топик "Смена x86 Quik 7.27.2.1 на x64 Quik 8.4.1.6. Пляски вокруг DLL", где кратко рассказывалось как перекомпилировать проект С++ с платформы х86 на х64. Надеюсь, что у вас все уже получилось или получится.
Но я «крутой» программист, и, естественно, у меня вначале вообще ничего и никак не получалось. А так как проект большой, да еще и непонятно в чем дело, а своими экспериментами я могу вообще все испортить, то решил сделать маленькую простенькую DLL LuaProba.dll, на ней отработать переход на х64, и потом перенести это в большой проект.
Привожу код С++ DLL целиком:

// LuaProba.cpp: определяет экспортированные функции для приложения DLL.
//

#include "stdafx.h"
#include <stdio.h>
#include <string.h>

//=== Необходимые для Lua константы ============================================================================//
#define LUA_LIB
#define LUA_BUILD_AS_DLL

//=== Заголовочные файлы LUA ===================================================================================//
extern "C" {
#include "Lua\lua.h"
#include "Lua/lauxlib.h"
}

static int forLua_TestFunc(lua_State *L) // Возвращает заданный текст
{
        const char *cc = "Привет из C/C++ и от меня 2 раза"; //str.c_str();
        lua_pushstring(L, cc);
        return(1);
}

//= == Регистрация реализованных в dll функций, чтобы они стали "видимы" для Lua == == == == == == == == == == == == == == == ==//
static struct luaL_reg ls_lib[] =
{
        { "TestFunc", forLua_TestFunc },
        { NULL, NULL }
};

//=== Регистрация названия библиотеки, видимого в скрипте Lua ==================================================//
extern "C" LUALIB_API int luaopen_LuaProba(lua_State *L)
{
        luaL_openlib(L, "LuaProba", ls_lib, 0);
        return 0;
}

Весь проект DLL для VS 2015 можно скачать по ссылке - 

( Читать дальше )

Ну что продолжим?

Скользящее окно(Moving Windows)

В заголовке я привел дословный перевод. Если кто меня поправит, и другой термин применяется — то спасибо.

Смысл скользящего окна– с каждым новым значением функция пересчитывается за заданный период времени. Этих функций большое количество. Для примера: rolling.mean(), rolling.std(), которые чаще всего и используют при анализе движения акций. rolling.mean() — это обычная скользящая средняя, которая сглаживает краткосрочные колебания и позволяет визуализировать общую тенденцию.

# Выделяю скорректированную цену закрытия 
adj_close_px = sber['Adj Close']

# Вычисляю скользящую среднию
moving_avg = adj_close_px.rolling(window=40).mean()

# Вывожу результат
print(moving_avg[-10:])

Дальше построим график, чтоб лучше понять то, что получается в результате работы данной функции:

# Вычисление короткой скользящей средней
sber['40'] = adj_close_px.rolling(window=40).mean()

# Вычисление длинной скользящей средней
sber['252'] = adj_close_px.rolling(window=252).mean()

# Построение полученных значений
sber[['Adj Close', '40', '252']].plot(figsize=(20,20))

plt.show()

( Читать дальше )

Сегодня дали логин-пароль для Quik. Quik 8.4.1.6. Номер и атрибуты счета пока не прислали, сказали через пару дней.
Сегодня настраивал и тестировал под фьючерсы и опционы. Вроде почти все ОК.
Исключение — после перезапуска самостоятельно не возобновляются потоки данных в таблицах обезличенных сделок. Нужно открывать настройки таблиц и щелкать ОК. Неудобно, но пока таблиц мало, это терпимо. Пока не знаю, м.б. чего еще настроить надо.
Теперь надо перекомпилировать софт под х64 и все проверять-настраивать.

ЗЫ И еще новость для юзеров Lua-QLua. Quik в ближайшее время переводится на версию Lua 5.3. На новых версиях Quik часть старых и самописных индикаторов, скриптов и ТС перестанет работать. Необходимо будет их доработать под версию Lua 5.3.
Новость на сайте Quik - https://forum.quik.ru/forum10/topic5119/

Возможно, не все знают про нелинейные эффекты грека Веги и волшебные свойства грека Воммы. По нынешним волатильным временам, когда вола ходит туда-сюда на десятки процентов — эти эффекты могут значительно повлиять на финрез при торговле волатильностью. Хочу поделиться своим видением — может кому будет интересно. А может кого убережет от опасной позиции с неоправданным риском.

Итак, рассмотрим проданный стрэдл:



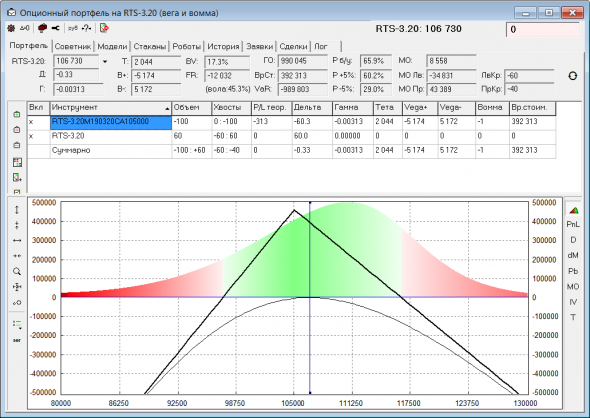
Это обычный профиль PnL, который рисуют все опционные программы. Фактически, это зависимость PnL позиции от первого момента (M1) распределения вероятностей, где окажется цена БА на экспирацию (вон оно на заднем фоне профиля). M1 = текущей цене БА. Т.е. мысленно двигаем все распределение влево-вправо (меняем M1) и считаем, как изменится PnL позиции при этом. Но, когда торгуем волатильностью, влияние первого момента ведь стараемся исключать используя дельтахедж (ДХ). И в большей степени нас должен интересовать профиль PnL от второго момента распределения (M2). Именно от него зависит финрез торговли волатильностью. Фактически, M2 почти тоже самое, что IV на центре улыбки (IVC). Смотрел на истории, специальным образом нормированный M2 (на цену БА и время до экспы) коррелирует с IVC почти 100%.

Если у нас есть опционная модель, в которой можно точечно менять второй момент, то легко посмотреть профиль PnL от изменений M2. Я использую замечательную модель Курбаковского, в которой главный параметр mI — как раз и отвечает за второй момент. Поэтому добавил в своей программе отрисовку такого профиля. И вот что рисует для проданного стрэдла:

( Читать дальше )

В прошлой статье рассмотрено как можно получить информацию по финансовым инструментам. Дальше будет опубликовано несколько статей о том, что первоначально можно делать с полученными данными, как проводить анализ и составлять стратегию. Материалы составлены на основании публикаций в иностранных источниках и курсах на одной из онлайн платформ.

В этой статье будет рассмотрено, как рассчитывать доходность, волатильность и построить один из основных индикаторов.

import pandas as pd
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt

sber = yf.download('SBER.ME','2016-01-01')

Доходность

Данная величина представляет собой процентное изменение стоимости акции за один торговый день. Оно не учитывает дивиденды и комиссии. Его легко рассчитать используя функцию pct_change () из пакета Pandas.

Как правило используют лог доходность, так как она позволяет лучше понять и исследовать изменения с течением времени.

# Скорректированая цена закрытия`
daily_close = sber[['Adj Close']]

# Дневная доходность
daily_pct_change = daily_close.pct_change()

# Заменить NA значения на 0
daily_pct_change.fillna(0, inplace=True)

print(daily_pct_change.head())

# Дневная лог доходность
daily_log_returns = np.log(daily_close.pct_change()+1)

print(daily_log_returns.head())

( Читать дальше )

Последние несколько месяцев время от времени начинал времени ломать голову над одной задачкой.
Суть в следующем.
Я сделал скрипт на питоне, на основе торговых данных пишет заявки в tri файл квиковский.
Чтоб заявку создать нужно принять решение на основе каких то данных из таблиц квика (например исполнилась какая то ранняя заявка, или банально цена дошла до нужного уровня, и т.п.)
Данные из таблиц квика, как известно, встроенными методами можно экспортировать через ДДЕ сервер, или в базы данных через ODBC.
То есть — для этого не надо обладать знаниями по программированию, это простые, очевидные способы, доступные всем, у кого установлен квик.
Я выбрал способ по ODBC, и пользуюсь им.
Связка работает стабильно, ничего не рушится, правда пару раз за несколько месяцев зависал сам квик из за того, что кончалась оперативная память (сервер слабенький у меня).

Но у такой связки есть слабое место, приходится в питоне запускать таймер, по кjторому питон опрашивает базу данных.

( Читать дальше )

Приветствую!))

                Появилось немного времени….решил поднять свои прошлые и текущие наработки. Подгрузил в ТС лаб и глянул что как по факту отработало на текущем рынке.

                Одна из не новых идей работы на прорыв волатильности. Сейчас использую ее для управления позицией в опционных конструкциях. Так же она стоит в портфеле алгоритмов

Ниже моя динамика работы опционами + данный алгоритм управление позицией (не путать с дельта хеджированием)

http://ranking.moex.com/strategy/opcionnaya-strategiya

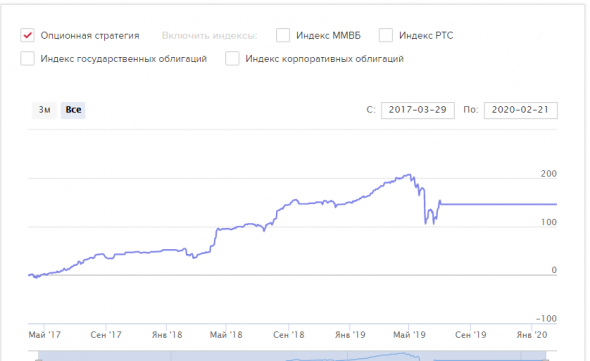
                Конечная просадка связана чист с технической невозможностью закрытия позиции из за повышения ГО биржи. И она восстановлена за 2,5 мес, но Мосбиржа перестала вести трансляцию данного счета (видимо из за большой волатильности счета).  Что бы не повторять моих ошибок советую ГО открывать не более 50%.

( Читать дальше )

В обсуждении прошлого топика совместно с коллегами мы пришли к выводу, что необходимым и достаточным условием безарбитражности в опционах европейского типа является колл-пут паритет

Call-Put=C-S*(1+R)^-1

где

Call – цена опциона колл со страйком S;

Put – цена опциона пут со страйком S;

С – текущая цена базового актива (БА, предполагается, что в активе нет купонов и дивидендов);

Собственно, рассуждения в рамках безарбитражности приводят нас к условию, что среднее относительного приращения цены БА до экспирации  равно R.

А что получается при колл-пут паритете, когда то же самое среднее в 20 и более раз больше R?

Сразу сделаем предположение, как у Блэка-Шоулза, что мы всегда можем занять любую сумму под ставку R.

Рассмотрим для простоты актив, который на любую будущую экспирацию имеет два равновероятных исхода: +30% и -10%, а R положим равным 1%.

Для простоты также будем считать, что 0.99*1.01=1, т. е. все в расчетах будем округлять до 0,1%.

( Читать дальше )

О чудесах календарного спреда фьючерсов уже доложено в статье некого 3Qu. smart-lab.ru/blog/586202.php

Поэтому сразу приступим к разоблачению. Какая проделана работа.
В Qukk'е на QLua написан монитор, который с 2020.01.17 по 2020.02.06 каждые 200 мсек записывал в текстовый файл офера и биды RIH0 и RIM0. Эти данные представлены как стандартный файл котировок Метастока, где Open = Bid(H0), High = Ask(H0), Low = Bid(M0), Close = Ask(M0).
Программа WealthLab показывает график этого файла, не понимая его значения. Но мой скрипт на C# по этим данным строит другие графики:


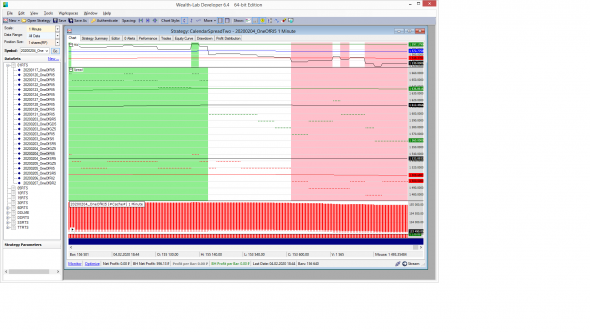
Две точечные линии, зелёные и красные ступеньки, в середине центральной панели:
1) SpreadLong = Ask(H0) — Bid(M0).
2) SpreadShrt = Bid(H0) — Ask(M0).
По цене SpreadShrt приходится продавать спред фьючерсов, когда он дорог а по цене SpreadLong — покупать спред, когда он подешевл.
Чтобы определить, дорог спред или дёшев, строим скользящие средние  с горизонтом 10 мин (серые линии)

( Читать дальше )