Свенсен Дэвид Ф., легендарный управляющий эндаументом Йельского университета, на мой взгляд, незаслуженно мало известен  в России. Он подробно, местами слишком подробно разбирает, как должен строить свой портфель частный долгосрочный инвестор, как им управлять для того, чтобы получить качественный долгосрочный результат. 
В книге рассматривается, из каких компонент может и должен состоять портфель, какие активы стоит туда включать, а какие не стоит, как нужно ребалансировать портфель и почему. 
Ясно, что российская действительность отличается от американской и выбор активов у нас несколько иной. Но принципы анализа остаются верными и у нас. Я купил эту книгу много лет назад и с тех пор в продаже её не видел. Возможно, у кого-то есть ссылка на электронную копию. Если так, пожалуйста, выложите такую ссылку в комментарии к моему сообщению.
Секреты стабильно высокой доходности:
www.ozon.ru/context/detail/id/4136008/

Зачитался, я тут на днях про робастную регрессию, и очень мне захотелось «пощупать» этого зверя хоть в каком нибудь виде на графике в Квике.

Выбрал наипростейшую — "Оценочная функция Тейла – Сена"

Эта оценочная функция может быть эффективно вычислена и она нечувствительна к выбросам. Она может быть существенно более точна, чем неробастный метод наименьших квадратов для несимметричных и гетероскедастичных данных и хорошо конкурирует с неробастным методом наименьших квадратов даже для нормально распределенных данных в терминах статистической мощности.
Метод признан «наиболее популярной непараметрической техникой оценки линейного тренда»

Сказано — сделано.

( Читать дальше )

Как говорится, трудно уснуть, пока в интернете кто-то не прав.

Случайны ли эти самые тренды? Таки нет вопроса более актуального на сегодняшний день:)

Возьмем часовую историю за 10 лет и проведем тот самый технический анализ: выделим все серии подряд идущих белых (черных) баров. Далее будем считать, сколько у нас получится серий из 1 белой (черной) свечи, сколько из двух, трех и т.д. Для сбербанка получается следующая картина:


























Зеленым цветом окрашены серии растущих баров, черным — падающих. И, о, чудо! Серий из двух баров почти ровно в 2 раза меньше, чем серий из 1 бара… а серий из 3 баров опять же в два раза меньше, чем серий из 2 баров и т.д. Паскаля, Ньютона, Да Винчи сюда....

В общем, вполне себе такое случайное блуждание за 10 лет с точки зрения орлов и решек. Кстати, эта картина одинакова для всех бумаг, которые я посмотрел, и не зависит от объема торгов. Везет тому, кто знает о завтрашнем аресте Ходорковского и идет шортить акции Юкоса… для него никаких случайностей нет.

( Читать дальше )

Прежде чем анализировать данные, применять супер волшебные методы и способы анализа давайте посмотрим на  природу  данных с биржи.

1. Базовый  поток  данных —   это  поток ордеров ( заявок). Следствием  потока  заявок, после сведения  биржевым движком,  является  поток  сделок. Одной  заявке которая  приводит к  появлению сделки  соответствует,  от  одной  до  нескольких сделок ( а  иногда и  сотни  сделок на одну  заявку).

2. Поток заявок является  нестационарным. Следствие потока  заявок — сделки, также являются  нестационарным потоком данных. В настоящее время  нет методов  позволяющих из  нестационарного потока  получить стационарный.

3. Тем не менее мы с  вами используем очень много самых разных методов остационаривания. Любой временной ряд имеет амплитуду, частоту, период, фазу. В нашем случае  все  эти параметры нестационарны. Пример стационарного ряда — синусоида. Все  параметры такого ряда  стационарны.

( Читать дальше )

Всех приветствую!

Сегодня искал в интернете книгу Эрнеста Чана «Algorithmic Trading: Winning Strategies and Their Rationale».
И наткнулся на гитхабе на большой сборник книг по различным областям и наукам, включая трейдинг и деривативы.
Правда все книги на английском. Но настоящему трейдеру ближе таки buy/sell))

https://github.com/spinlockirqsave/books

Добавляйте в закладки. Ставьте лайки)

Упрощенный алгоритм вычисления приближенного значения размерности Минковского, для ценового ряда.

Краткая справка:

Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:

• где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.

Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов. 

( Читать дальше )

Я не буду рассказывать, что такое опцион (ну, типа, «это контракт, дающий покупателю право, но не обязанность бла-бла-бла»), надеюсь все интересующиеся знают, или слышали, или могут в Вики посмотреть. Сразу покажу, как определяется его цена. Да, еще 2 замечания. Я говорил, что нам не понадобится математика уровня выше 9-го класса школы — извините, соврал. :) Но 11-классник уже справится. И второе: вы не научитесь торговать опционами по этим заметкам, придется читать книжки.

Представим очень простую (скажем прямо — примитивную) модель изменения цены акции. Каждый день цена акции может измениться только на 1 рубль, вверх или вниз. Вот так:

И мы хотим купить опцион колл с ценой исполнения (страйком) 100. Как понять, сколько нам платить продавцу, чтобы цена была «справедливой»?

1. Максимальная прибыль в этой модели (которая на картинке) — 6 рублей. Дороже 5.99 рублей покупать смысла точно нет.
2. За 0 рублей нам его тоже не продадут.

( Читать дальше )

Добрый вечер.

При одних и тех же периодах — намного информативней и интересней...

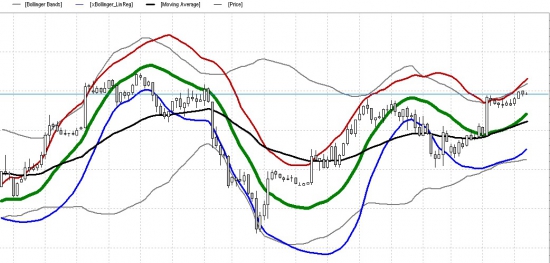
Settings = 
{
        Name = "xBollinger_LinReg",
        period = 40,
        deviation=2,
        line=
        {
                {
                        Name = "xBollinger_LinReg",
                        Color = RGB(0, 0, 255),
                        Type = TYPE_LINE,
                        Width = 2
                },
                {
                        Name = "xBollinger_LinReg",
                        Color = RGB(192, 0, 0),
                        Type = TYPE_LINE,
                        Width = 2
                },
                {
                        Name = "xBollinger_LinReg",
                        Color = RGB(0, 128, 0),
                        Type = TYPE_LINE,
                        Width = 6
                }
        
        }
}


function c_FF()
        
        local AMA={}
        local CC={}
        
        return function(ind, _p,_ddd)
                local period = _p
                local index = ind
                
                local vol = 0
        
                local sigma = 0
                local sigma2 = 0

                local aav = 0
                local bb = 0
                local ZZZ = 0

                                        
                if index == 1 then
                        AMA={}
                        CC={}
                        
                        CC[index]=(C(index)+H(index)+L(index))/3
                        AMA[index]=(C(index)+O(index))/2
                        
                        return nil
                end
                
                ------------------------------
                AMA[index]=AMA[index-1]
                CC[index]=(C(index)+H(index)+L(index))/3

                if index < (_p) then return nil end
                                
                period =_p
                if index < period then period = index end
        --------------- 
                sigma=0
                sigma2=0
                aav=0
                ZZZ=0
                for i = 0, period-1 do
                        ZZZ=CC[index+i-period+1]
                        aav=aav+ZZZ
                        sigma=sigma+ZZZ*(-(period-1)/2+i)
                        sigma2=sigma2+(-(period-1)/2+i)^2
                end
        bb=sigma/sigma2
        aav=aav/period
                
        AMA[index]=aav+bb*((period-1)/2)
                
                sigma=0
                sigma2=0
                sigma3 = 0
                for i = 0, period-1 do
                        ZZZ=CC[index+i-period+1]
                        sigma2=aav+bb*(-(period-1)/2+i)
                        sigma=sigma+(ZZZ-sigma2)^2

                end
                sigma=(sigma/period)^(1/2)
                                                                
                        return AMA[index]-sigma*_ddd,AMA[index]+sigma*_ddd, AMA[index]
                        
        end
end


function Init()
        myFF = c_FF()
        
        return 3
end
function OnCalculate(index)
        
        
        
        return myFF(index, Settings.period,Settings.deviation)
        
                
end

Предыдущая часть: smart-lab.ru/blog/337952.php

Для всех QUIKеров в свободное пользование индикатор «Параболическая регрессия/тренд» (LUA).

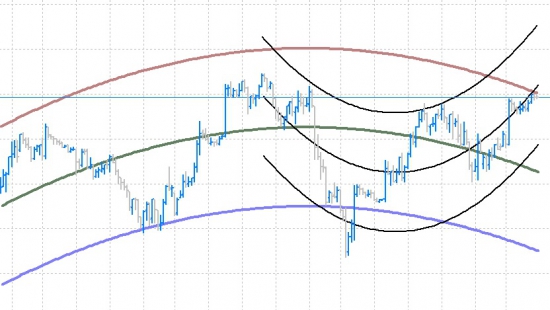
Settings = 
{
        Name = "xLinRegP",
        period = 128,
        deviation=2,
        line=
        {
                {
                        Name = "xLinRegP",
                        Color = RGB(128, 128, 255),
                        Type = TYPE_LINE,
                        Width = 4
                },
                {
                        Name = "xLinRegP",
                        Color = RGB(192,128,128),
                        Type = TYPE_LINE,
                        Width = 4
                },
                {
                        Name = "xLinRegP",
                        Color = RGB(96, 128,96),
                        Type = TYPE_LINE,
                        Width = 4
                }
        
        }
}

----------------------------------------------------------
----------------------------------------------------------
----------------------------------------------------------
function cached_FF()
        local AMA={}
        local CC={}
        local II2 = 0
        local II4 = 0
        
        
        return function(ind, _p,_ddd)
                local period = _p
                local index = ind
                
                local vol = 0
        
                local sigma = 0
                local sigma2 = 0
                local sigma3 = 0
                local sigma4 = 0

                local aav = 0
                local aa = 0
                local bb = 0
                local cc = 0
                local ZZZ = 0
                local ttt = 0


                                                
                if index == 1 then
                        
                        AMA={}
        
                        CC={}

                        CC[index]=(C(index)+H(index)+L(index))/3
                
                        AMA[index]=(C(index)+O(index))/2
                
                                II2=0
                                II4=0
                        for i = 0, period-1 do
                                ttt=(-(period-1)/2+i)^2
                                II2=II2+ttt
                                II4=II4+ttt^2
                        end
                
                        return nil
                end
                
                ------------------------------
                
                        AMA[index]=AMA[index-1]
                        ----------------------------------
                        CC[index]=(C(index)+H(index)+L(index))/3
                        ---------------------
                


                        
                if index < (Size()-2) then return nil end
                
                ----------------------------------------------------


                sigma=0
                sigma2=0
                sigma3=0
                sigma4=0
                aav=0
                ZZZ=0
                for i = 0, period-1 do
                        ZZZ=CC[index+i-period+1]
                        
                        aav=aav+ZZZ
                        sigma=sigma+ZZZ*(-(period-1)/2+i)
                        ttt=(-(period-1)/2+i)^2
                        sigma3=sigma3+ZZZ*ttt
                end
                
                ------------------------
        bb=sigma/II2
    cc=(sigma3-aav*II2/period)/(II4-II2*II2/period)
        aa=(aav-cc*II2)/period
        aav=aav/period
                
        AMA[index]=aa+bb*((period-1)/2)+cc*((period-1)/2)^2             ------- парабола
        -------------------------------

                
                sigma=0
                sigma2=0
                sigma3 = 0
                for i = 0, period-1 do
                        ZZZ=CC[index+i-period+1]
                        sigma2=aa+bb*(-(period-1)/2+i)+cc*(-(period-1)/2+i)^2           ------- парабола
                        sigma=sigma+(ZZZ-sigma2)^2

                end
                sigma=(sigma/period)^(1/2)
                
                for i = 1, period-1 do
                        ZZZ=aa+bb*(-(period-1)/2+i)+cc*(-(period-1)/2+i)^2
                        SetValue(index+i-period+1, 3, ZZZ)
                        SetValue(index+i-period+1, 2, ZZZ+sigma*_ddd)
                        SetValue(index+i-period+1, 1, ZZZ-sigma*_ddd)

                end     
                        SetValue(index+0-period+1, 3, nil)
                        SetValue(index+0-period+1, 2, nil)
                        SetValue(index+0-period+1, 1, nil)
        
                
                ----------------------------------
                                                                
                        return AMA[index]-sigma*_ddd,AMA[index]+sigma*_ddd, AMA[index]
                        
        end
end
----------------------------    ----------------------------    ----------------------------
----------------------------    ----------------------------    ----------------------------
----------------------------    ----------------------------    ----------------------------

function Init()
        myFF = cached_FF()

        return 3
end

function OnCalculate(index)
        
        return myFF(index, Settings.period,Settings.deviation)
        
                
end