Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

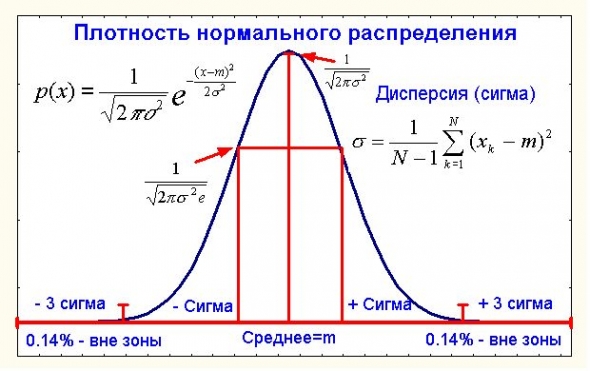
Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

Сегодня воскресенье, извините если напишу о не о.чем.Вам трейдинг приносит счастье? вы всегда счастливы когда юзаете на граали  и выкладываете свои граали? А я застал время рабочих… отдыхающих в бассейнах и банях за счет государства, и это не в москве… а на дальнем востоке… хабаровск, арсерьев, амурская область поселки  екатеринославка, васильевка… не алкаши, очень правильный народ… и дети были правильные… ходили в советские школы.
ВОПРОС-У ВАС машина времени… хотели бы вы вернуться ну в год 75? У меня все есть, все это значит все ,… по любым меркам… квартиры машины… и тд, блин но я значит успешный человек! Да -скажут многие -ты же не мог этого иметь пока капитализм не наступил@… ребята… я бы со своими мозгами жил еще бы лучше… главное люди… были другими… они были советскими.Они были живыми и девушки настоящими… Мы офигеть что потеряли, и продолжаем терять… из поколения в поколение

Оптимальные стратегии

Обозначения:

C_t – цена актива;

d_t=(C_t-C_t-1)/C_t-1;

d_t – случайна и имеет безусловное распределение P(d_t), т. е. точного прогноза этой величины одновременно во все (!) моменты времени не существует (отметим, что существование точного прогноза в отдельные моменты времени не означает детерминированности- антипода случайности, которая подразумевает наличие точного прогноза в любой(!) момент времени) ;

L_t – вся информация, известная к моменту времени t;

Р(d_t/L_t-1) – условное распределение d_t по L_t-1;

P(d_t,,d_t-1)  - безусловное распределение пары (d_t,,d_t-1);  

E_t g(d_t) – среднее функции g(x) по распределению Р(d_t/L_t-1);

E g(d_t,d_t-1)  среднее функции g(x₁,x₂) по распределению Р(d_t,d_t-1);

M_t – оценка самофинансируемого (без вводов-выводов) портфеля в момент времени t;

( Читать дальше )

В связи с тем, что за последние несколько дней я получил ряд писем с вопросами о моих результатах и видео от Гусева, что " Горчаков не зарабатывает 15 лет", я сделал таблицу своих помесячных доходностей по стандарту GIPS на личном счете, где торговались только мои алгоритмы 



Справочно в последнем столбце таблицы я привожу и поправочные коэффициенты для своих результатов в компаниях, где управлял деньгами. Любой желающий может через коэффициенты получить мои реальные результаты для работодателей. Из таблицы видно, почему на круглом столе алготрейдеров весной 2014 я совершенно откровенно заявил, что если б не третье марта, то я бы всерьез раздумывал на смене деятельности в ближайшие месяцы. Что касается результатов, то я уже писал, что 2011 и 2014 стали для меня годами упущенных возможностей. Первый из-за «фильтра шортов», второй из-за отсутствия Si в портфеле. А вот в 2013-м я ничего изменить не могу. В 2012-м могло бы быть лучше, если б то, что начал с июля, было бы с начала года. Но тогда я об этом не знал, а потому это нельзя считать «упущенной возможностью», если конечно не считать «задержку» с модификациями с апреля 2011-го. Но о прострации, постигшей меня после большой июльской «пилы» 2011-го, я тоже писал. И только «околорынок» в виде подготовки курса в декабре 2011-го вывел меня из этой прострации.

( Читать дальше )

Тут все спорят, что надо делать и как «перезагрузить» экономику страны...

Но первопричина всего — колоссальные диспропорции при переспределении доходов внутри страны за последние 10 лет

смотрим первый график:


В течении многих лет население копило «избыточные доходы» (социальные бонусы от нефтедолларов) на банковских счетах...

И когда эти накопления доросли до существенных величин…

( Читать дальше )

Я прочел эту книгу в 2009-м году и она перевернула мой мозг. Она большая — 800 страниц, я все время хочу перечитать ее снова, но не хватает времени. Это самое лучшее, что я читал из художественной литературы. Я всегда и всем советую обязательно прочесть эту книгу, особенно карьеристам, перфекционистам, профессионалам своего дела, людям, настроенным на достижение успеха. Обычно считаетя, что у Рэнд более известен роман «Атлант расправил плечи». Я могу точно сказать, что Источник лучше, и читать его интереснее, тем более он написан позднее, после Атланта.

Книга про архитектора, который всегда делал только то, что считал нужным. Его выгнали из университета за свободомыслие, его никто не хотел брать на работу, профессиональное сообщество насмехалось над ним, потому что он строил особенные дома, которые выбивались из общепринятых догм. Он сидел в офисе неделями напротив телефона, читал книги и ждал, что позвонит какой-то клиент.

Я ни разу не читал ничего такого, чтобы могло меня так заставить восхищаться величием личностей, описанных в книге. 
Кроме того, в книге описана совершенно красивая любовная история.
Читая книгу, просто нельзя не восхититься интеллектом самой писательницы — Айн Рэнд. 

Книга вдохновляет, дает пинка, мотивирует, меняет сознание. Перечитывать ее тоже стоит, чтобы напоминать себе, что ты создан для чего-то большего, чем просто сидеть круглыми днями за компом

Заблуждение первое: «Акционер – собственник доли имущества акционерного общества».

Ничего подобного. Собственность в ее нормальном понимании, а не в новомодных «теориях» — это три «кита»:

— владение;

— пользование;

— распоряжение.

Вот Вы купили акций и по отношению к чему Вы получили такие права? К станку, прилавку, «трубе» или помещению? Ни к чему из перечисленного. Вы получили такие права только по отношению к акциям, т. е. Вы собственник акций, а не имущества.

А что дает акция? Только право участия в собрании акционеров и голосования по вопросам, отнесенным уставом обществам к решениям данного собрания.  Т. е. Вы стали собственником этого права и не более того.  Как минимум нормальное законодательство обязует общество относить к правам собрания акционеров, утверждение устава общества, назначение размеров дивидендов, как части чистой прибыли и выбор совета директоров и(или) исполнительных органов власти общества, если уставом общества совет директоров не предусмотрен. По каким еще вопросам Вы приобрели право голосования? Это уже зависит от устава конкретного общества.

( Читать дальше )

Пока делал рассылку, наткнулся на опрос на прошлой неделе:
 
Получается, что сами же люди на смартлабе меня из указанных лиц больше всего ненавидят:) Я не буду умолять достоинств вышеуказанных лиц, но конечно немножко загрустил. Вот смотрю на себя со стороны:

• в пирамиды никого не завлекал, напротив, предостерегал как мог
• обучение никому не впаривал и ложной нажежды никому не дарил (было 3 ученика, грешен, но сугубо индивидуально)
• денег ни чьих на рынке не терял 
• стараюсь вон, смартлаб постоянно улучшаю, чтобы вам было удобно общаться
• пишу статьи в финансовый словарь, надеюсь, что кому-то пригождается инфа
• собираю трейдеров-инвесторов вместе, устраиваю общение, организуя конференции
• рассылки делаю, шоб вы ничего полезного не пропустили, обзоры пишу, чтоб читать было интересно
• да, не очень хорошо торгую последние 2 года, зато  никого не обманываю, пишу ток все как есть

А люди почему-то недолюбливают:)) Что делаю не так?:)
 

я не являюсь специалистом в области геополитики. все нижеперечисленное — моя попытка разобраться в ситуации для самого себя.

Я бы рад забыть и про США и про Украину, но тема сейчас не выходит из информационного пространства, являясь постоянным раздражителем моего сознания.

При этом, ощущение, что американцы не настроены на торможение конфликта. Вот возьмем новость о том, что Тоомас Ильвес (през.Эстонии) попросил Обаму укрепить присутствие НАТО в стране. У них уже 4 американских истрибителя, а будет еще 6.

Как это понимать? Американские военные истребители в 150 км от Санкт-Петербурга! Может они думают, что Путин пойдет завоевывать Эстонию? С кем они там воевать собрались? Да и самое-то главное, они за кого Путина принимают? Ни одного намека на агрессивную внешнюю политику (в отличие от США).

Ранее по ситуации в Украине я пытался анализировать сугубо факты: 3 марта 2014 11 марта 2014

Дальнейшее развитие событий подтвердило основной вывод: переворот в Украине полностью подготовлен, профинансирован и исполнен властями США. Зачем властям США сдалась Украина? Сами украинцы наверное думают, что они особая нация, раз США обратили на них внимание. нефти в Украине нет. Граждане Украины — один из самых бедных народов мира. Нахрена США жертвовать $5 млрд на развитие демократии в Украине? Почему США не пожертвовали $5 млрд на развитие демократии в Северной Корее?

Ну допустим США хотели разместить в Украине:

• военно-морскую базу в Крыму
• ПРО
• наступательные ядерные вооружения и т.п.

США в общем и так это все могут сделать с территорий Польши, и стран Балтии, которые почему-то намного больше любят американцев, нежели Россию. В этом смысле, вероятно, Украина не является каким-то критически значимым звеном. Хотя конечно, если разместить американские ядерные ракеты в 500 км от Москвы, это бесспорно был бы весомый аргумент:)

//замечу, что приведенные выше факты явно свидетельствуют о том, что США выступает агрессором по отношению к России и власти США провоцирует конфликт с Россией// Логика подсказывает, что Украина не сильно нужна США как таковая:

• не сланцевый газ там особо не нужен
• не нужна особо территория Украины как аэродром и база ВМФ США

Более того, США не питают иллюзий, что "Украина — проклятая земля". И тем не менее, ощущение что у Обамы, Керри, Нулланд, Байден и т.п. других забот нет, кроме как вписываться за Украину.

Какой-то логический диссонанс. 


( Читать дальше )

Итак, господа, уже 10 дней мы с Вами живем в совершенно непонятном никому банковском ваккууме. Каждый из нас получает по нескольку раз на дню различные версии «черных списков», анализирует их, пересылает друзьям и знакомым.
При все при этом общество разделилось на два лагеря:
— «пессимистов» мол хуже уже не будет,
И «оптимистов» — будет, будет ;)
Одни из нас убеждают, мол не гоните волну, не усугубляйте ситуацию и все такое..
Другие бегут снимать все что есть и прятать под подушку...
Третьи ехидно наблюдают со стороны и радуются что у них ничего нет в банках.
Давайте вернемся лет на 10 назад к тому счастливому, повторюсь СЧАСТЛИВОМУ времени когда не было Системы Страхования Вкладов!!!!
И как-то жили все прекрасно, и банки работали и большие и малые, и вклады люди размещали по совету друзей и знакомых. А главное все задумывались о том, что они делают.
Любой физик прекрасно осознавал, что неся вклад в более доходный банк он берет на себы дополнительный риск.
Банкир понимал сколько денег ему надо и куда он их будет вкладывать и от этого выстраивал кредитно-депозитную политику.
И бизнес маломальски кредитовался (по куда меньшим ставкам кстати), и машины-квартиры в кредит давали (конечно серьезно анализируя заемщика).
И тут 2004 год… Даешь АСВ!!! Проведем жесткий отбор в систему!!! Враг не пройдет!!!
Неразумные декларативные действия тогда создали миникризис на почве «пустят в ССВ или нет» и погубили Гуту и чуть не похоронили Альфу.
Начали вроде неплохо критерии отбора, проверки и все такое.
Самои интересное, что мелкие и средние банки особо и не стремились в ССВ, ибо прекрасно понимали — КРЕДИТОВАНИЕ БИЗНЕСА ЗА СЧЕТ РЕСУРСОВ ФИЗИКОВ до хорошего не доведет.
Аналитики еще тогда предсказывали — что экспоненциальный рост вкладов, защищенных госгарантией это таже ГКО, только более долгосрочная.
на 2000 год сколько было вкладов — 400 млрд
на 2013 — 17 трл руб это средства физических лиц
К 2013 году в АСВ пустили всех кто просился...
Все!!! стоп дальше расти некуда!!!
Достаточно физикам снять 20% вкладов (вполне реалистичный сценарий) и ВСЯ СИСТЕМА рухнет… будет 98 год, даже хуже
То что сейчас происходит в банковском секторе своего рода «Стресс-тест» всей системы, и те кто его не пройдет виноваты в этом в первую очередь САМИ.
Отркроем любой «черный список» — ну ведь реально большинство из представленных там банков так или иначе замешаны в сомнительных операциях — что они не понимали чем занимаются ??? отлично понимали!!!
Привлекая вклады под 12-13% в год при нулевом росте экономики на что надеялись обе стороны — на русское авось ???
Кредитуя девелоперские проекты со сроками окупаемости в десятиление за счет остаков на текущих счетах — это кто и чем думал ???
Сколько нужно бизнесцентров и кому их сдавать в аренду ???
Всем было пох… АСВ все покроет…
Подождем увидим, кто там кого и чем покроет.
К сожалению можно констатировать мелкого и среднего банковского бизнеса больше нет… Халява кончилась! 
Но почему-то не все готовы с этим смириться...