В продолжении начатого эксперимента по вложению в стейблкоины, а именно попытки на них заработать, публикую отчёт по истечению первых трёх месяцев. Подробное описание эксперимента доступно здесь.

В разрезе отдельных историй:

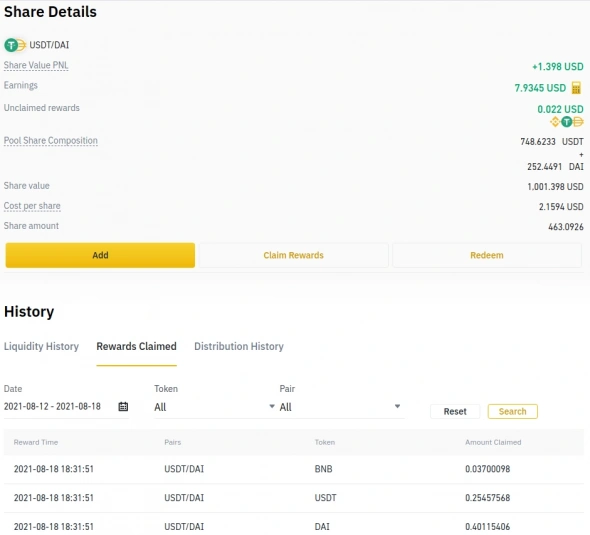
1) Пул ликвидности Binance Liquid Swap USDT-DAI

За прошедшее время было начислено 0,03700098 токена BNB, который был продан за 14,75 USDT. Кроме того было начислено 0,25 USDT и 0,41 DAI. За счёт работы пула наша доля также выросла в переоценке на 1,39 USD.
Итог в пуле 0,25+0,41+14,75+1,39=16,8 USD (здесь и далее я буду использовать USD как аналог стоимости 1 стейблкоина и 1 доллара)

В этом посте я хочу рассмотреть вариант арбитражной стратегии, и протестировать его на чувствительность к проскальзыванию, чтобы понять возможность применения.

Далее будут приведены мои субъективные умозаключения.

Для начала перечислю виды арбитража, которые я знаю:

1. Арбитраж одинаковым активом между разными биржами. Сложность работы по этой технологии заключается в том, чтобы разместить торговый сервер между двумя биржами так, чтобы задержки пакетов между биржами были одинаковыми.
2. Арбитраж между активом и его деривативом.
3. Статистический арбитраж между коррелируемыми активами.
4. Календарный арбитраж.

Момент, который объединяет эти стратегии, состоит в том, что торговая позиция выставляется всегда одновременно по двум инструментам в противоположные стороны (если активы прямо скоррелированы, и в одинаковые стороны в ином случае).

Все эти арбитражные стратегии в основном относятся к классу рыночно-нейтральных «mean reversing» стратегий, потому что не следуют за трендом, а пытаются вернуться к некой справедливой цене актива (та же трендовая составляющая), выставляя позиции против отклонения от тренда, хотя, конечно, можно придумать и трендовые стратегии, использующие актив-«поводырь» для прогнозирования тренда.

Чуть больше недели назад выступил на AllDerivatives. Рассказывал о моем личном опыте работы с эволюционирующим ИИ и о попытках применения в торговле. Материала засунул, как сейчас понимаю, избыточно много, в результате выступление получилось слегка скомканным, затянутым и поверхностным, но на удивление, люди, присутствовавшие на выступлении говорят, что получилось интересно.

Во-первых, не ждите глубоких секретов, не ждите граалей. Более того, было больше всего про биологию, меньше про программную реализацию и совсем чуть-чуть про трейдинг.

Во-вторых, это не те дроиды, которых вы ищите это совсем не то, что мы используем, во всяком случае на чужих деньгах в реальной торговле.

Но рассказывал я о том, что реально делал в разное время на протяжении многих лет, что меня давно очень интересует и в чем, смею надеяться, чуть-чуть понимаю ;)

Презу на экране видно плохо, но она есть по ссылке в описании.

--[[
параметры: 
Procent - процент зигзага 
--]]
Settings={
Name="ZIGZAG_Templ",
Procent=2,
    line=                                     
                {  
					{  
                        Name = "cur1",
                        Type =TYPE_LINE,
                        Width = 2,
                        Color = RGB(0,0, 0)
                    }				
                }
}

function Init()
  
  y1 = nil
  y2 = nil
  x1 = 1
  x2 = 1
       
  return 1
  
end

function OnCalculate(index)

  de = Settings.Procent

  vl = C(index)
  if index == 1 then 
	y1 = vl
    y2 = vl
  else   
	  if C(index) > y1*(1+de/100) and y1 < y2 then 
	    x2 = x1
	    y2 = y1	
	    x1 = index 
	    y1 = C(index)		
      else 
	    if C(index) > y1 and y1 >= y2 
		then 
	      x1 = index 
	      y1 = C(index)	  			  
	    end 		
	  end 	

	  	  		
	  if C(index) < y1*(1-de/100) and y1 > y2 then 
	    x2 = x1
	    y2 = y1
	    x1 = index 
	    y1 = C(index)				
      else 
	    if C(index) < y1 and y1 <= y2 
		then 
	      x1 = index 
	      y1 = C(index)	  			  
	    end 		
	  end 	
	  	  		
	end 	
  
  if x1 ~= index then 
    curfrom = x1
	curto = index
  else 
    curfrom = x2
	curto = x1
  end 

  if curto ~= curfrom and curfrom ~= nil and curto ~= nil then 
    if C(curto) ~= nil and C(curfrom) ~= nil then 
      k = (C(curto)- C(curfrom))/(curto- curfrom)  
      for i = curfrom, index  do
        curv = i*k + C(curto) - curto*k  		          
	    SetValue(i, 1, curv)
      end   	
	end 
  end 
  
  return vl
 
  
end

Ранее подробно писал о способе уменьшить налог при торговле на брокерском счете — сальдировании убытков по ценным бумагам: зачесть убыток по одним бумагам в счет прибыли по другим, чтобы не платить налог.

Сегодня расскажу о том, как это сделать, если открыты счета у разных брокеров.

Итак, если вы торгуете через нескольких брокеров, по итогам года можно сложить между собой финансовые результаты, полученные у каждого из них.

Один брокер не сможет учесть операции, совершенные через другого брокера, но это можно сделать самостоятельно: подать декларацию и вернуть излишне уплаченный налог.

Что делать:

1️⃣ Каждый из брокеров самостоятельно рассчитывает прибыль и уплачивает с нее налог.

2️⃣ Берем у каждого из брокеров справки 2-НДФЛ о суммах доходов и расходов

Если кого вдохновило сообщение smart-lab.ru/blog/680086.php, тому не обойтись без книги «NUMERICAL RECIPES. The Art of Scientific Computing. Third Edition». Качайте, пока дают

www.e-maxx-ru.1gb.ru/bookz/files/numerical_recipes.pdf
Бесплатные исходники к ней github.com/blackstonep/Numerical-Recipes
Программа svd.h из этого набора решает задачу наименьших квадратов для построения индикатора полиномиальной регрессии вместо примитивных скользящих средних.
Хорошее объяснение математической подоплёки в книге «Машинные методы математических вычислений. Форсайт, Малькольм, Моулер» en.booksee.org/book/445129
Ещё лучше — «Линейная алгебра и её применения» Гилберт Стренг
fileskachat.com/download/20151_887581203f10b39b3d7f6b84caf48a63.html
«Linear Algebra and Its Applications 4ed»
www.astronomia.edu.uy/progs/algebra/Strang- Linear_algebra_and_its_applications.pdf

Для использования программы svd.h из «NUMERICAL RECIPES» нужны тривиальные дополнения — транспонирование и перемножение матриц. Набор программ можно дополнить самодельным файлом utils.h и разместить в нём такой код:

#include <assert.h>
template <class T>
class NRdiagonal: public NRvector<T> { using NRvector<T>::NRvector; };

template <typename T>
void Multiply (const NRdiagonal<T>& a, const NRvector<T>& b
    ,NRvector<T>& c) {
  int m = a.size();
  assert (m == b.size());
  c.resize (m);
  for (int i = 0; i < m; ++i)
  c[i] = a[i] * b[i];
}
template <typename T>
void Multiply (const NRmatrix<T>& a, const NRvector<T>& b
    ,NRvector<T>& c) {
  int m = a.nrows(); int n = a.ncols();
  assert (n == b.size());
  c.resize (m);
  for (int i = 0; i < m; ++i) {
    c[i] = 0;
    for (int j = 0; j < n; ++j)
      c[i] += a[i][j] * b[j];
  }
}
template <typename T>
void Transpose (const NRmatrix<T>& a, NRmatrix<T>& b) {
  int m = a.nrows(); int n = a.ncols();
  b.resize (n, m);
  for (int i = 0; i < n; ++i)
    for (int j = 0; j < m; ++j)
      b[i][j] = a[j][i];
}
template <typename T>
void PrintVector (char* hdr, const NRvector<T>& vec) {
    cout << hdr << '\n';
  for (int i = 0; i < vec.size(); ++i)
    cout << " " << vec[i];
  cout << '\n';
}

Привет! Бегло полистал SL и обнаружил, что книжные обзоры делятся на 2 типа – инвесторские и хардкорное алго (HFT и опционы). Промежуточный вариант попытаюсь закрыть данным постом. По уровню сложности книги в обзоре находятся между зубодробительной подборкой от Eugene Logunov https://smart-lab.ru/blog/534237.php и приятным чтивом по фундаментальным стратегиям.

1)    Lasse H. Pedersen – Efficiently Inefficient

Отличная книга и №1 по соотношению польза/сложность. Автор показывает, как кванты тестируют и отбирают стратегии в портфель. Условно ее можно разделить на 4 части: арбитраж, факторные стратегии, глобал макро и технические моменты запуска и финансирования фонда. HFT и опционные стратегии упоминаются вскользь. Наверное, книга подойдет и для совсем начинающих, т.к. все метрики (вплоть до волатильности) и базовые концепции раскрываются с 0.

LHP – один из боссов крупного хедж фонда в Гринвиче, но в отличие от Далио или Дракенмиллера, еще и хардкорный академик. Поэтому в книге любое утверждение подтверждается ссылками, а для глубокого погружения есть отличный список первоисточников. Понятно, что никаких секретов своего работодателя LHP не раскрывает, но профильные главы для меня оказались полезными в плане идей + отсылки туда, где копать глубже.

Выводы

1. В общем рейтинге с учетом всех рынков первое место занял метод усредняющий три прогноза: г-на Твардовского, г-на Механизатора и экспоненциальный.

2. Подход г-на Твардовского с подобранным мной множителем подтвердил свою прогнозную силу на различных рынках. Для российского рынка акций и фьючерсов данный метод оказался наилучшим. Для commodities, индексов и американских акций этот подход вошел в тройку лучших. Для дневного таймфрейма подход г-на Твардовского оказался самым точным для выбранной группы из пяти активов.

3. Экспоненциальный метод также доказал свою полезность, заняв третье место в общем рейтинге. Для американских акций прогнозы в рамках данного подхода оказались самыми точными. 

4. Подход г-на Механизатора с выбранным мной множителем уступил лидерские позиции другим методам, но оказался полезен при совместном использовании с другими способами .

5. Для часового таймфрейма популярные подходы Parkinson, Yang-Zhang, Rogers-Satchell и Garman-Klass в большинстве случаев оказались хуже даже базового метода расчета исторической волатильности. Впрочем, для дневного таймфрейма показатели этих методов (в частности, подхода