Избранное трейдера Дмитрий Власов
Американский SPY и другие популярные ETF теперь в России!
- 19 ноября 2018, 16:31
- |
Учитывая пожелания институциональных и частных инвесторов и проведя опрос на сайте Кабинет инвестора https://investcab.ru/ru/, 16 ноября 2018 года была расширена линейка ETF доступных в рамках торгово-клиринговой системы Ассоциации «НП РТС». Добавлены в систему наиболее востребованные биржевые фонды:

SPY — является одним из крупнейших и наиболее активно торгуемых ETF в мире, дает доступ к самому востребованному бенчмарку - S&P 500. Этот биржевой фонд заслуженно популярен среди долгосрочных консервативных инвесторов, для которых важно точное следование за индексом, но наибольшую популярность он снискал среди активных трейдеров. Анализ торговли показывает небольшое время нахождения в позиции по этому активу большинства трейдеров в течение дня. SPY – обладает огромной ликвидностью, спреды между покупкой и продажей очень узкие – при большом количестве сделок потери на спреде минимальны.

( Читать дальше )
- комментировать
- ★28
- Комментарии ( 11 )
Как составить консервативный портфель
- 06 ноября 2018, 19:15
- |
Перед любым инвестором стоит важный вопрос: сохранить или приумножить? Любые вложения – это риски. Разница лишь в том, насколько вы к ним готовы. Если цель инвестирования – получить доходность выше, чем в банке, и сберечь свои нервы, составляйте консервативный портфель.
В этой статье рассказываем, как сохранить средства, минимизировав потери. Вы узнаете, на что обращать внимание и с помощью каких активов диверсифицировать риски.
Не кладите все яйца в одну корзину
Главный совет начинающему инвестору: «Помни о диверсификации!».
Любые инвестиции всегда связаны с рисками, поэтому в первую очередь старайтесь максимально обезопасить личный капитал. Добиться этого можно, составив диверсифицированный портфель.
Окей, гугл, как это делать?
Диверсифицировать риски — значит распределить инвестиции внутри портфеля в разные рынки, отрасли, инструменты. Цель — максимально снизить их зависимость друг от друга. Зависимость в финансовой теории называется «корреляция». Простыми словами — это то, насколько равно- или разнонаправленно двигаются цены на выбранные активы в зависимости от ситуации на рынках.
( Читать дальше )
Переоптимизация?
- 01 ноября 2018, 19:08
- |
Добавили тут на днях в ТСЛаб возможность штатным образом случайные числа получать. В связи с чем возникла идея устроить небольшой стресс тест стратегиям, заменив имеющееся управление позицией выходом по рынку через случайное количество баров.
Я считаю, что то, что принято называть переоптимизацией, кроется как раз в управлении позицией. Если подумать, то в точке входа подгонки не может быть по определению. Ведь задача как раз найти такое соотношение параметров, которое работает в нашу сторону как можно чаще. И чем сильнее будет подгонка под идеальный сетап — тем лучше, тем точнее мы опишем желаемую ситуацию. А вот с выходом всё иначе. Тут уже есть конкретные точки входа и конкретный набор свечей на истории… И вот как раз тут может быть подгонка параметров стопа, тейка, трейлинга и т.п. под эти конкретные ситуации..
Подгонка может быть столь сильной, что за ней вполне может спрятаться полное отсутствие положительного смещения вероятности в точке входа…
Вот мне и стало интересно, что если выход из позиции будет произвольным? Тогда, по идее, значительный перевес положительных исходов может намекать на наличие положительного смещения вероятности в точке входа.
Для эксперимента взял 2 стратегии на Ri. Одна, проверенная девятью месяцами реала и подтвердившая свою профпригодность на сегодняшний день, и другая — простая, состряпанная на скорую руку, стратегия по скользяшкам с максимальным фиттингом (оптимизация точки входа одновременно с трейлингом по широкому диапазону параметров на всей истории за один проход). Везде стоит комиссия 20п.
Итак, изначальная эквити «проверенной» стратегии выглядит так:
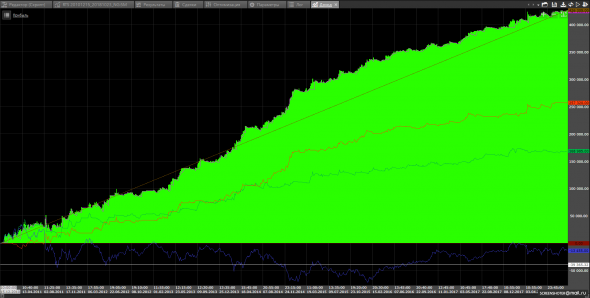
( Читать дальше )
Роботы как инструменты Трейдера.Ч.1.
- 31 октября 2018, 22:22
- |
Пост собрал аж 615 плюсов 330 комментов.
Комменты я до конца так и не дочитал, ну а по самому посту так и хочется сказать, — вроде взрослые люди, а всё в сказки верите..
99% роботов, которые валяются, или продаются на просторах инета, это так сказать, ДВУмерные роботы.
Всю информацию для принятия решения они черпают из графика ЦЕНА+Время одного инструмента.
Со стороны любой такой бот напоминает червяка, который выёжывается на плоскости Евклидова пространства, хотя кукловод живет в №-мерном Гильбертовом.
Понятно, что рано или поздно любой подобный двумерный червяк (бот) будет раздавлен рыночным сапожищем.
Ну хотя бы потому, что двумерный бот не может ответить на простейший вопрос, — что происходит? Это евро растет или доллар падает?
Отсюда первый вывод, один бот в поле не воин.
Нужна согласованная работа нескольких ботов одновременно (джаз банда), или одного, но работающего на нескольких инструментах одновременно.
( Читать дальше )
Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год!
- 17 октября 2018, 13:53
- |
Теперь новая напасть. Как владелец иис, я возвращаю 52 000 рублей каждый год по ндфл. Делается это достаточно просто (по идее, и в этом году решили сделать ещё проще вроде как. в прошлом такой проблемы не возникало):
1.Вы сдаете декларацию 3-НДФЛ через тот же личный кабинет.
2.Она проходит камеральную проверку, и налоговый орган выдает решение о возврате (смотри скрин 1).

( Читать дальше )
О «теореме Ферма» теории вероятностей или о нормальности «бытия» (много буков)
- 16 октября 2018, 16:41
- |
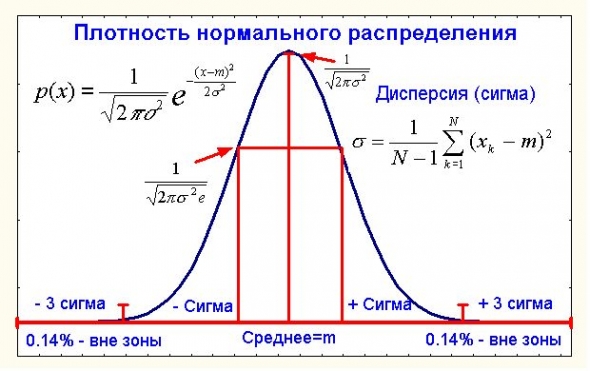
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении
А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам. Что такое центральная предельная теорема в ее классическом виде?
Пусть нам дана некоторая сумма большого числа случайных величин Х=х1+…+хN где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.
Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если xi – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x
( Читать дальше )
Синтаксис языка MQL4
- 12 октября 2018, 14:37
- |
Синтаксис — это такой набор правил, которые определяют как из символов алфавита языка собирать слова и предложения, которые образуют правильно структурированную и корректно работающую программу или её фрагмент. Таким образом, наблюдение за набором любого корректного кода, можно одновременно считать и изучением синтаксиса языка.
Однако, согласно справке в разделе посвящённом синтаксису языка предлагается рассмотреть:
- комментарии;
- идентификаторы;
- зарезервированные слова.
Комментарии — это пометки к определённым строкам или целым кускам исходного кода программы, в которых программист разъясняет себе, что происходит на данной строке или в данном фрагменте программы. Комментарии не являются частью исполняемого кода. Они нужны для того, чтобы в программе было проще ориентироваться, особенно если её потребовалось модифицировать спустя какое-то время после написания. Комментарии позволяют быстро вспомнить, что делает программный код.
( Читать дальше )
Автоматизация трендов | обновление
- 25 сентября 2018, 16:22
- |
Заменил линейную регрессию на экспоненциальную, подшаманил с алгоритмами гомоскедастичностью и робастностью, прочие баги...
В общем продолжу традицию экипировки молодых бойцов ЛЧИ )))
Каналы
было - https://smart-lab.ru/blog/386529.php
стало
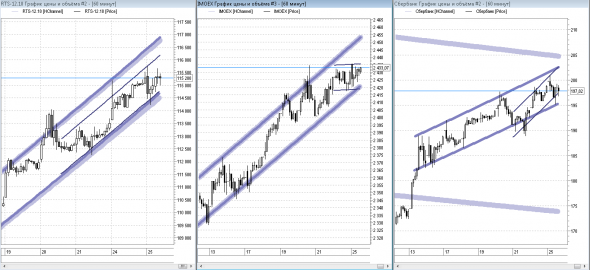
( Читать дальше )
S#.Data от StockSharp и Финам, попытка сделать автообновление истории.
- 25 сентября 2018, 11:55
- |
Стиль автора сохранен.
Добрый день! Эта история о том, как я работал с продуктом S# — S#.Data, также известной как Гидра.
Идея была таковой: обеспечить автоматическую загрузку и обновление исторических данных (минутные свечи) с Финама по сотне акций и двум десяткам фьючерсов. Решено было реализовать эту идею с помощью источника «Финам» и задачи «Экспорт (авто)». С первых минут работы с сим шедевром стало ясно, что придётся помучиться. Первым делом загрузил все инструменты, доступные Гидре (с трудом, ибо Гидра начала бунтовать, пришлось перезапустить эту программу), после добавил примерно сотню акций и около двадцати фьючерсов, настроил кое-как источник и задачу, установил начальную дату для загрузки историй.
( Читать дальше )
курсы Василия, желающие приходите.
- 19 сентября 2018, 16:49
- |
номер раз

номер два

( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал