Я тут недавно постил свою методику заработка пенсионных баллов на онлайн-проектах, как трейдеру не остаться без пенсии после слива депозита. У людей в комментариях были вопросы по сайтам, и как я на них зарабатываю. Я сделал вывод, что многим интересна тема инвестиций в сайты и заработка на сайтах.

Могу кратенько спалить немного инфы о своем основном текущем интернет-проекте и заработке с него. Трейдерам будет полезно (все равно торчишь у монитора, сливаешь, хоть бы что полезное сделал). Стебусь, конечно. Ну а если серьезно, сайты позволяют серьезно диверсифицировать доходы и снизить личные финансовые риски в рамках трейдерского лайфстайла (кровать-монитор-кровать — вы же не про Майами, тачки и телок сейчас подумали?)

Как заработать на своем сайте

Начну с вводной для тех, кто в танке. В интернете есть миллионы и миллионы сайтов. Глобально они делятся на 2 типа. Половина из них что-то продает, половина ничего не продает. Те, которые ничего не продают, называются

( Читать дальше )

1. В папке с Квиком создаем директорию LuaIndicators.
2. В этой папке создаем файл gazp_usd.lua, туда записываем:

Settings = 
{
   Name = "GAZPROM_USD",
   tag = "GAZP",
   tag1 = "GAZP_USDRUB",
   line=
   {
      {Name = "line1", Color = RGB(0, 0, 255), Type = 1,Width = 1}
   }
}

vPrice=1;

function Init()
   return 1
end

function OnCalculate(index)
	local vOutFlag=0;
	local vGazp =(getCandlesByIndex(Settings.tag, 0, index-1, 1)[0].close or 1) ;
	local vUSDRUB=(getCandlesByIndex(Settings.tag1, 0, index-1, 1)[0].close or 1);
	if vGazp>0 then
		vOutFlag=1;
	else
		vOutFlag=0;
	end;
	if vUSDRUB>0 then
		vOutFlag=1;
	else
		vOutFlag=0;
	end;
	if vOutFlag > 0 then
		local Out = vGazp/vUSDRUB;
		vPrice=Out;
	end;
	return  vPrice
end

3. В Квике создаем график с курсом доллара (USDRUB_TOM).
4. К графику добавляем график Газпрома (ГАЗПРОМ ао).
5. Идем в настройки графика, в разделе «Дополнительно» указываем «Идентификатор»: GAZP -для графика с ценой Газпрома, GAZP_USDRUB -для графика с курсом.
6. Добавляем индикатор (выбираем из выпадающего списка GAZPROM_USD).

7. Уменьшаем ненужные поля. Если график не отобразился — даблкликаем на графике — жмем «Применить»:

( Читать дальше )

Продолжение.

Один из простых признаков, отличающих случайную последовательность от рыночных данных — характер реакции на уровни или на то, что обычно называют уровнем (вступление для любителей рассуждений о рыночном шуме).

Уровни видит большинство и обычно как-то реагирует, поэтому логично создание системы, эксплуатирующей поведение торгующих вблизи уровня.

Cознательно выбран тест Si, ходившего в небольшом диапазоне, вместо традиционного RI.

На картинке — результат теста простой системы, входящей «на отбой» и «на пробой» уровня с фиксированными стопами и лотностью. Она вполне надежно сливает, теряя на спреде и комиссии.


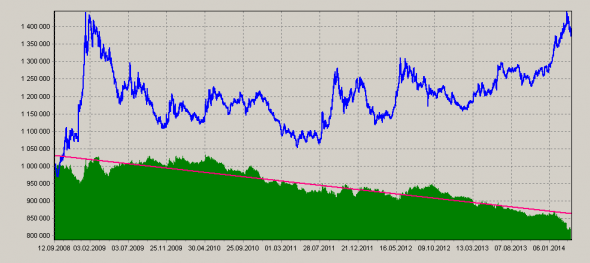
Первая модернизация — добавление алгоритма, распознающего разные ситуации, ведь люди ведут себя в зависимости от наблюдаемого. Первые варианты использовали только относительно простой подсчет амплитуд и касаний, но на момент тестирования (2014) получалось программно различать более десятка типов уровней, с весьма тонкими различиями. Самое грубое деление на «плохие и хорошие» немедленно перевело систему в доходные и резко уменьшило чувствительность к оптимизации.

( Читать дальше )

    Может кому будет интересен скрипт на QLUA, который выступает простым бенчмарком ОФЗ с постоянным купоном к ставке ЦБ.
Основные параметры доходность и премия к ставке ЦБ, с учетом дюрации.
Скрипт не работает онлайн (оперативность тут не принципиальна), при запуске собирает параметры в таблицу и выводит на экран.
В дальнейшем планируется эти данные использовать для анализа премии доходности по дюрации для муниципальных и корпоративных облигаций к ОФЗ.




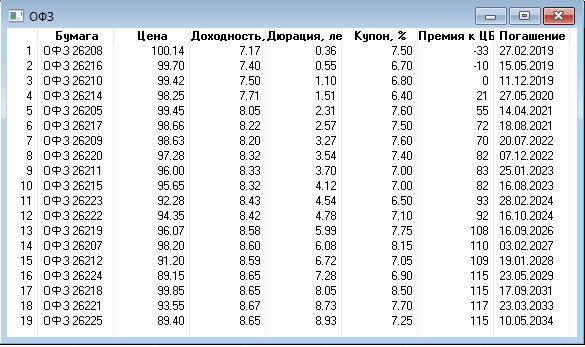
    Код скрипта на github (на github две версии одна в utf-8 для просмотра и основная версия в win1251, т.к. quik понимает только его):
github.com/trantor77/lua_scripts/boundsOFZ.lua

    Код скрипта:

--переменные
keyRateCB = 7.5
classCode = "TQOB"

function CreateTable()
    t_id = AllocTable()
    AddColumn(t_id, 0, "Бумага", true, QTABLE_STRING_TYPE, 15)
    AddColumn(t_id, 1, "Цена", true, QTABLE_DOUBLE_TYPE, 15)
    AddColumn(t_id, 2, "Доходность, %", true, QTABLE_DOUBLE_TYPE, 15)
    AddColumn(t_id, 3, "Дюрация, лет", true, QTABLE_DOUBLE_TYPE, 15)
    AddColumn(t_id, 4, "Купон, %", true, QTABLE_DOUBLE_TYPE, 15)
    AddColumn(t_id, 5, "Премия к ЦБ, бп", true, QTABLE_INT_TYPE, 15)
    AddColumn(t_id, 6, "Погашение", true, QTABLE_STRING_TYPE, 15)
    t = CreateWindow(t_id)
    SetWindowCaption(t_id, "ОФЗ")
end

function string.split(str, sep)
    local fields = {}
    str:gsub(string.format("([^%s]+)", sep), function(f_c) fields[#fields + 1] = f_c end)
    return fields
end

function getParamNumber(code, param)
    return tonumber(getParamEx(classCode, code, param).param_value)
end

function formatData(prm)
    return string.format("%02d.%02d.%04d", prm%100, (prm%10000)/100, prm/10000)
end

CreateTable()

arr = {}
sec_list = getClassSecurities(classCode)
sec_listTable = string.split(sec_list, ',')
j = 0
for i = 1, #sec_listTable do
    secCode = sec_listTable[i]
    securityInfo = getSecurityInfo(classCode, secCode)
    short_name = securityInfo.short_name
    if short_name:find("ОФЗ 26") ~= nil then
        j = j + 1
        r = {}
        r["short_name"] = short_name
        r["price"] = getParamNumber(securityInfo.code, "PREVPRICE")
        r["yield"] = getParamNumber(securityInfo.code, "YIELD")
        r["duration"] = getParamNumber(securityInfo.code, "DURATION")/365
        couponvalue = getParamNumber(securityInfo.code, "COUPONVALUE")
        couponperiod = getParamNumber(securityInfo.code, "COUPONPERIOD")
        r["coupon"] = ((365/couponperiod) * couponvalue)/10
        r["bonus"] = (r["yield"] - keyRateCB)*100
        r["mat_date"] = getParamNumber(securityInfo.code, "MAT_DATE")
        table.insert(arr, j, r)
    end
end

table.sort(arr, function(a,b) return a["duration"] < b["duration"] end)

for j = 1, #arr do
    row = InsertRow(t_id, -1)
    SetCell(t_id, row, 0, arr[j]["short_name"])
    price = arr[j]["price"]
    SetCell(t_id, row, 1, string.format("%.2f", price), price)
    yield = arr[j]["yield"]
    SetCell(t_id, row, 2, string.format("%.2f", yield), yield)
    duration = arr[j]["duration"]
    SetCell(t_id, row, 3, string.format("%.2f", duration), duration)
    coupon = arr[j]["coupon"]
    SetCell(t_id, row, 4, string.format("%.2f", coupon), coupon)
    bonus = arr[j]["bonus"]
    SetCell(t_id, row, 5, string.format("%.0f", bonus), bonus)
    mat_date = arr[j]["mat_date"]
    SetCell(t_id, row, 6, formatData(mat_date), mat_date)
end

Решил написать обзор по компании НМТП — крупнейшей портовой группе в РФ.

Сразу скажу, какой-то особой инвестиционной идеи я здесь пока не вижу, не смотря на то, что НМТП — это первоклассный актив. Я предпочитаю подождать и буду покупать эту акцию, если цены еще ощутимо припадут (с пика 2017 г. они упали уже на треть). На уровне ~5 руб., например, этот актив будет выглядеть уже очень привлекательно. Пока я потихоньку покупаю Интер РАО (инвест идею писал раньше)

Саммари по НМТП

1) Порт развивается, финпоказатели растут, он не такой дешевый как в 2015-2016 гг., но нельзя сказать что дорогой. Еще немного снижения и актив будет оценен очень привлекательно, возможно куплю его вместо НКХП (но только после дополнительного падения)

2) Транснефть купила 25% с существенной премией к рынку и стала контролирующим акционером. Очевидно, что ей не интересны ненефтяные сегменты порта (непрофильный бизнес), поэтому тут может быть какая-то сделка в будущем (в т.ч. спин офф?).

( Читать дальше )

Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

Давно известно, что если вы хотите купить какую-то акцию дешевле — продайте на нее пут не в деньгах. Например хотите сбер по 180? Продайте 180й пут. Если цена упадет ниже 180 — то вы получите акцию по 180 и еще премию по путу. (например 2) и таким образом эффективная цена покупки будет 178. Ну, а если цена не упала — то получите просто истекшую премию в размере 2, что в пересчете на ГО довольно неплохая доходность. Пример выше — условный, надо смотреть на цены, страйки, волатильность. Но есть одно простое правило — путы лучше продавать тогда, когда рынок уже припал и вола подскочила и часть падения уже пройдена. (Так, сейчас кто-то бросится писать коммент про мой 2008й год. Да, такое бывает. Но сейчас этих предпосылок, вроде как, нет).
Чем еще хорошо продавать путы? что если акция болтается в диапазоне, то вы собираете премию. Обычный владелец стока при неизменной (почти) цене акции получит лишь дивиденды, а вы — опционную премию. (правда не будет дивидендов)

Но тут возникает два момента — первый, с опционами не все знакомы и не все связываются и второй — не на каждый инструмент есть опцион. Поэтому сейчас я расскажу стратегию торговли, для которой не нужны опционы, но суть ее особо не поменяется. Более того, добавятся дивиденды.

( Читать дальше )

Поступила информация, что население смартлаба за последние годы несколько обновилось, и кому-то может оказаться полезным узнать как можно просрать миллиарды на опционах, как можно на салфетках объяснить опционы гуманитарию или как написать робота, который с капиталом 3 млн р держал 15% объемов торгов в опционах RI. В общем иногда полезно перечитывать хорошо забытое старое (сейчас даже сам удивляюсь, как это меня хватило на все это буквосложение)



Гном. Или как трейдер обанкротил банк.

Глава первая и вторая

Глава третья и четвертая

Глава пятая и шестая


Гном 2. Возвращение.

Глава первая

Глава вторая и третья

Глава четвертая и пятая

( Читать дальше )

Как обогнать индекс (пример выигрышной торговой стратегии)

          В кругу экономистов бытует мнение, что обогнать фондовый индекс на длительной перспективе невозможно, и если вам удалось в какой-то определенный год вырваться вперед, получив прибыль гораздо выше той, которую продемонстрировал индекс акций, то в будущем неизбежно ваши результаты не превзойдут индекс, а могут оказаться только хуже него. Подобная точка зрения следует из гипотезы эффективного рынка. К сожалению, экономика отличается от математики тем, что строгое доказательство практически любого утверждения представляется невозможной задачей. Тем не менее, в данной статье мне бы хотелось привести пример одной из стратегий, которая способна обогнать индекс акций в длительной перспективе. Разумеется, я отдаю себе отчет в том, что не могу доказать это математически. Впрочем, в экономике практически везде используются различные гипотезы, которые невозможно доказать, например, почему-то принято  считать, что движение цен подчиняется нормальному распределению, и я что-то нигде не встречал какого-либо доказательства подобного утверждения. Тем не менее, именно на основе гипотезы о нормальном распределении была придумана знаменитая формула Блэка-Шоулза для оценки стоимости опционов, за которую ее авторы даже получили нобелевскую премию.

( Читать дальше )