Есть у меня один друг, который мощно трейдает. В эти выхи он овощ. Лежит и ничего не хочет.  Я грю: заежжай. А он: я ничего не хочу. 
Лично у меня есть объяснение, почему так происходит. 

У нормального человека в нормальной жизни деятельность строится на цикле — мотивация-удовлетворение. Вы чего-то захотели, вы начинаете что-то делать, вы добиваетесь этого, вы полчаете удовлетворение. Под этими явлениями есть вполне конкретные химические процессы, которые регулируются при помощи определенных гормонов (дофамин, серотанин, норадреналин). 

Моя недоказанная теория состоит в том, что во время торговли на все плечи, человек запускает в течение дня мощные циклы выброса этих гормонов. Поскольку эти действия многократно повторяются, организм привыкает к такому мощному стимулированию…  


( Читать дальше )

Предлагаю вашему вниманию простенький метод оценки стоимости опциона на центральном страйке исходя из текущей волатильности.

в качестве индикатора волатильности используем ATR (Average True Range), который доступен во многих торговых терминалах

По своей сути ATR показывает средний размер свечи (с учетом гэпов) за заданный период. Для расчетов желательно выбрать часовой таймфрейм и период кратный одному торговому дню (для ФОРТС 14, для FOREX 24).  В результате имеем среднее значение от максимума до минимума часовой свечи.  Зная это значение, и взяв на себя смелость предположить, что волатильность останется примерно такой же в интересующий нас будущий промежуток времени, мы можем посчитать ожидаемый размер «свечи» большего временного интервала:

ATR(N)= ATR(Н1)*КОРЕНЬ(N),  где N количество часов в свече большего временного интервала.

Тем самым мы поучили ожидаемое значение от максимума до минимума свечи в  N часов.

( Читать дальше )

Читая смартлаб, наткнулся на священный холивар инвестор-спекулянт. Имхо, этот холивар решается просто--трейдер должен владеть как краткосрочными, так и долгосрочными методами. Ну и всвязи с этим вспомнил свою статью пятилетней давности про инвестиционность. В принципе, почти со всем согласен и сейчас. Чтобы не загибла на просторах интернета, перепощу сюда. Оригинал: utkin.2stocks.ru/?p=443 

 Для зарабатывания денег на фондовом рынке нужно использовать некоторые связи между прошлым и будущим (см. http://www.2stocks.ru/utkin/?p=14). Наряду с трендовостью, связанной с истеричностью (и, как следствие, частичной предсказуемостью) толпы, есть еще одно свойство именно фондовых рынков, на основе которого могут быть выявлены искомые закономерности. Это свойство я называю инвестиционностью. Оно заключено в том, что в очень большом периоде времени фондовые рынки растут, то есть растет фондовый индекс. Для примера рассмотрим график индекса Доу Джонса за 80 последних лет:

( Читать дальше )

               Доверительное управление с помощью портфеля торговых роботов за март 2015 года принесло доходность +7.37%. Кривая доходности портфеля вышла на новые исторические максимумы (+180.7% за 2 года и 3 месяца).
 
              По итогу 1 кв 2015 счет прибавил на 13%. Январь, март в «плюсе», февраль в относительно маленьком «минусе»
В марте в работу было введено несколько новых алгоритмов,  в том числе  торговый робот Contra . Это позволит несколько сместить фокус с трендовых систем и повысить устойчивость всего портфеля торговых роботов в целом. Динамика доходности с начала 2013 года доступна по ссылке. Более подробную информацию по управлению высылаем на почту по запросу. Все результаты подтверждены брокерскими отчетами по каждому месяцу.

06.04.2015

В этот день результат нулевой, так как небыло позиций до 19:00. В 22:05 сформировал позицию на вторник такую: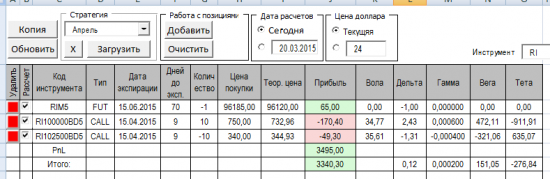
 

( Читать дальше )

Приветствую всех участников! Так, или иначе, но вчера пара евро-доллар пробила диапазон спроса 1,0774-1,0703. Остановки нисходящего движения практически не было. Сейчас пара придвинулась к ближней границы диапазона спроса 1,0650-1,0580.

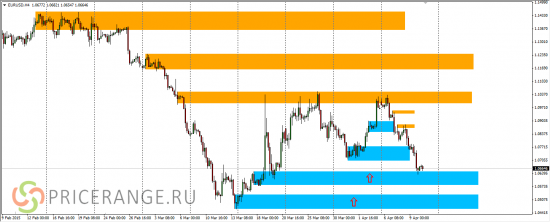
Диапазон спроса с Н4 является сильным. Но выше сформировался диапазон предложения 1,0730-1,0790. Его лучше посмотреть на часовом графике:

( Читать дальше )

Еженедельная аналитическая передача «Технический анализ. Владимир Гусев» на видеопортале трейдеров YouTrade.TV от 9 апреля 2015 г.

Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора 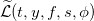, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью 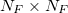, где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях,  в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в

( Читать дальше )

Константин Гринькин рассказывает про свое интеллектуальное дельта-хеджирование, которое не только хеджирует, но и зарабатывает деньги.


Пример работы дельта-хеджера тут:
 

Конференция смарталаба по трейдингу состоится 18 апреля