Избранное трейдера Павел М
Россия - худшая страна для инвестиций? Выводы для инвесторов
- 27 ноября 2018, 14:26
- |
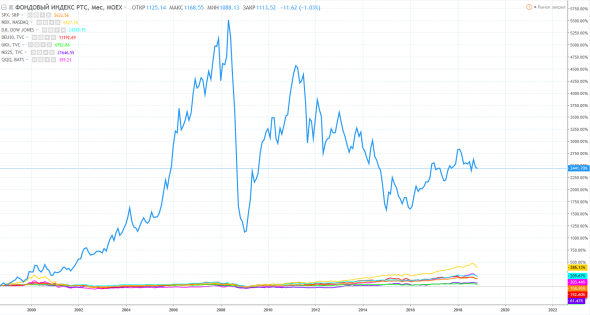
На картинке: индекс РТС рвет в клочья мировую экономику с суммарным ростом 2441% против ближайшего конкурента — индекса NASDAQ, растущего за тот же период всего на 385%.
Что это — магия цифр или легкий способ стать миллиардером? Давайте разбираться.
Пост призван систематизировать мои мысли о принципиальной целесообразности инвестиций в российский рынок в настоящий момент. Мы рассмотрим упрощенный анализ долларовой доходности инвестиций в популярные биржевые индексы начиная с 2000 года по настоящее время. Минимум букв, максимум статистики. Наверное, написанное дальше для большинства из вас будет очевидными вещами, но возможно какому-нибудь начинающему инвестору в российский рынок это позволит по-новому взглянуть на свою стратегию.
Индексы, участвующие в сравнении:
1) Индекс РТС (RTSI) — долларовый индекс 50 крупнейших эмитентов России (USD)
2) Индекс S&P 500 (SPX) — долларовый индекс 500 избранных эмитентов США (USD)
( Читать дальше )
- комментировать
- ★41
- Комментарии ( 81 )
Ничего не меняется
- 07 ноября 2018, 22:16
- |
Год-полтора назад и до недавних пор на смартлабе, а он, как ни крути, лакмусовая бумажка рфр, началось засилие постов инвесторов. Со стажем, неофитов, переквалифицировавшихся трейдеров и пр.
Рост будет, дивиденды рулят, портфель на 10-30 лет, за коррекцией идут новые высоты и остальное в том же духе.
Очередной сигнал окончания цикла — эйфория, уверенность, приход денег наслышавшихся о росте сбера клерков.
В октябре раздался звоночек. Тихий, как цунами в открытом море. Легкое ворчание есть, но скрежета зубовного ещё нет.
Инвесторы, бегите. Тихая гавань снова сколлапсирует, стоит только амерам нырнуть процентов на 15. А ведь медвежий цикл никто не отменял. И это не три планки на панике, а потом рост. Нет. Это год-два равномерного снижения самого большого рынка. И тогда инвесторам придётся несладко. Во всем мире, а в рф особенно.
В общем, как говорил триединый Козьма Прутков: «Бди!»
Как я за 2 года сделал финансовый сайт в 2 раза больше Смартлаба и [почти] ничего не заработал
- 27 октября 2018, 09:10
- |
Могу кратенько спалить немного инфы о своем основном текущем интернет-проекте и заработке с него. Трейдерам будет полезно (все равно торчишь у монитора, сливаешь, хоть бы что полезное сделал). Стебусь, конечно. Ну а если серьезно, сайты позволяют серьезно диверсифицировать доходы и снизить личные финансовые риски в рамках трейдерского лайфстайла (кровать-монитор-кровать — вы же не про Майами, тачки и телок сейчас подумали?)
Как заработать на своем сайте
Начну с вводной для тех, кто в танке. В интернете есть миллионы и миллионы сайтов. Глобально они делятся на 2 типа. Половина из них что-то продает, половина ничего не продает. Те, которые ничего не продают, называются
( Читать дальше )
Прикол с российской электрогенерацией
- 25 октября 2018, 11:38
- |

(см. табличку на смартлабе)
При этом стоимость строительства новых энергоблоков обычно где-то выходит под $1000/кВт.
Генерирующие компании на развивающихся рынках торгуются на уровне $1478/кВт, то есть более чем в 10 раз дороже, чем российские.
На развитых рынках, средний EV/кВТ составляет $2126.
Отчитаться по доходам, полученным на фондовом рынке в 2018 году, надо будет по новой форме
- 21 октября 2018, 20:00
- |
Добрый день!
Налоговая инспекция утвердила новую форму налоговой декларации 3-НДФЛ за 2018 год. Основание: приказ ФНС России от 03.10.2018 г. № ММВ-7-11/569@. Сам приказ пока не вступил в силу (начало действия документа – 1 января 2019 года). Скачать новую форму декларации можно будет позже.
Почему я обращаю внимание на этот документ? По завершении текущего 2018 года многие из вас будут обязаны отчитаться по полученным доходам, а кто-то будет претендовать на налоговый вычет. Давайте перечислим все возможные случаи, когда подается декларация 3-НДФЛ:
– получение дохода, из которого не был удержан налог налоговым агентом;
– получение дохода из-за рубежа;
– получение дохода от продажи имущества, находящегося в собственности менее трех лет;
– получение выигрыша;
– получение в подарок имущества не от близких родственников;
– необходимость получения налогового вычета в связи с расходами на приобретение или строительство жилья;
– необходимость получения налогового вычета в связи с расходами на лечение;
( Читать дальше )
Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год! Часть 2 - Чудеса в налоговой!
- 18 октября 2018, 17:56
- |
Начались чудеса с налоговой! Продолжение истории - Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год!
Вчера я написал пост, о том что случилось с моим заявлением в ИФНС 15 о возврате 52000 рублей по ИИС (заявление было от 21.08.2018). Сегодня мне на почту приходит письмо с ответом на данное заявление., хотя по закону я должен был получить ответ (если он требовался, например тот же отказ) не позже чем, через 30 дней.
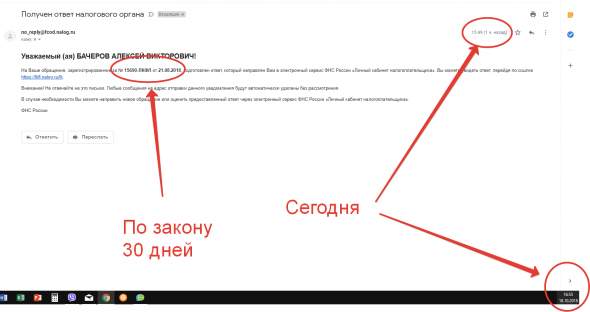
Напомню, что я писал письмо через сервис «Личный кабинет» — 01.10.2018 чтобы налоговая разобралась, что произошлом с моим заявлением от 21.08.2019, поскольку ни ответа не денег я не получил. Ответ на письмо от 01.10.2018 я получил вчера, он датирован 16.10.2018. Скрины приведены в предыдущем посте (https://smart-lab.ru/blog/499854.php). Получается, что ответ на само заявление о возврате я получаю позже, чем на письмо, в котором просил разобраться. Что я могу подумать в этот момент? Там будет примерно та же информация, т.е. год указан неправильно, и поэтому отказ (ровно как и в письме от 16.10.2018).
( Читать дальше )
Двигатель для авиалайнера МС-21 прошел сертификацию
- 18 октября 2018, 09:17
- |
Российский двигатель ПД-14 для перспективного среднемагистрального лайнера МС-21 получил cертификат.
министр промышленности и торговли Денис Мантуров:
«Фактически, получение cертификата типа подтверждает готовность ПД-14 к реализации и эксплуатации. Можно констатировать: успешно создан первый в современной России турбореактивный двигатель для гражданской авиации»
Следующим этапом станет валидация сертификата в Европейском агентстве авиационной безопасности.
«Реализация проекта позволит значительно увеличить долю российских комплектующих в конструкции перспективного среднемагистрального самолёта. Кроме того, будет создан базис для увеличения более чем в два раза продаж российских газотурбинных двигателей»
https://rns.online/industry/Dvigatel-dlya-rossiiskogo-lainera-MS-21-uspeshno-proshel-sertifikatsionnie-ispitaniya-2018-10-18/
Обещанный Манн-Уитни
- 17 октября 2018, 13:21
- |
smart-lab.ru/blog/499678.php#comment8969912
Исходные данные: закрытия дня с 07.12.2005 по 16.10.2018 для S&P500 и индекса Мосбиржи
VAR00003, если VAR00004=0: центрированные и нормированные приращения логарифмов индекса Мосбиржи
VAR00003, если VAR00004=1: центрированные и нормированные приращения логарифмов индекса S&P500
Результат
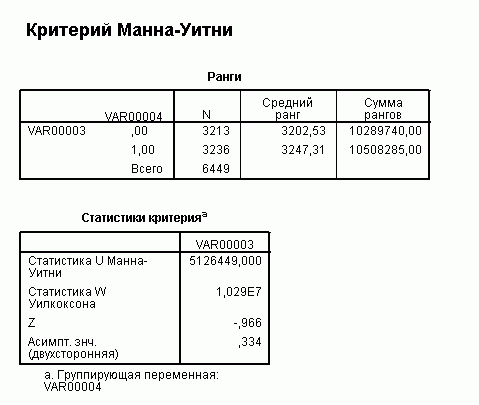
Итого: вероятность ошибиться, утверждая, что эти распределения разные, больше 0,334.
И вывод: выборочные распределения приращений логарифмов дневных значений индексов Мосбиржи и S&P500, вероятней всего, совпадают с точностью до среднего и дисперсии.
О «теореме Ферма» теории вероятностей или о нормальности «бытия» (много буков)
- 16 октября 2018, 16:41
- |
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении
А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам. Что такое центральная предельная теорема в ее классическом виде?
Пусть нам дана некоторая сумма большого числа случайных величин Х=х1+…+хN где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.
Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если xi – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x
( Читать дальше )
Стратегия инвестирования, которая даст вам больше (но это не точно)
- 16 октября 2018, 11:55
- |
Чем еще хорошо продавать путы? что если акция болтается в диапазоне, то вы собираете премию. Обычный владелец стока при неизменной (почти) цене акции получит лишь дивиденды, а вы — опционную премию. (правда не будет дивидендов)
Но тут возникает два момента — первый, с опционами не все знакомы и не все связываются и второй — не на каждый инструмент есть опцион. Поэтому сейчас я расскажу стратегию торговли, для которой не нужны опционы, но суть ее особо не поменяется. Более того, добавятся дивиденды.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал