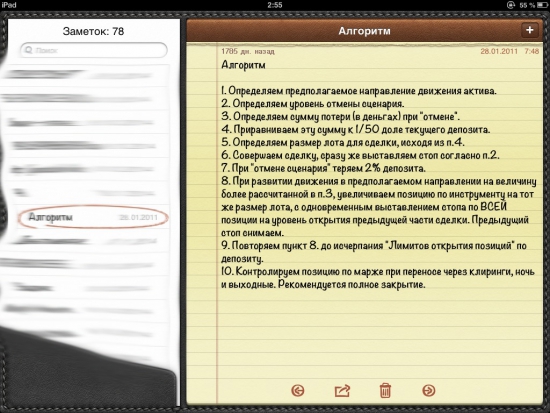
Алгоритм
Алготрейдинг. Робот-кусака на РТС. Ri long and short
- 10 марта 2016, 18:11
- |
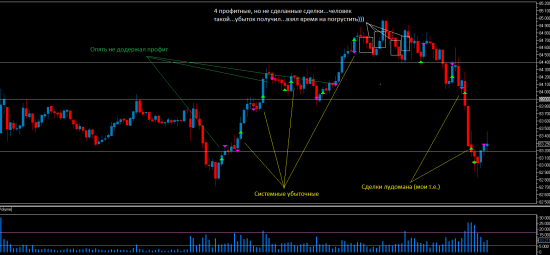
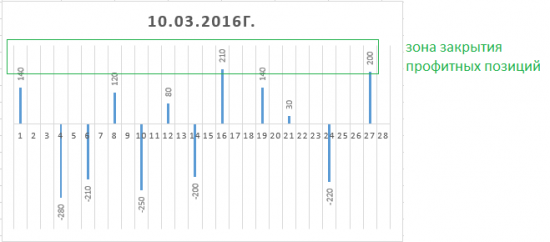
( Читать дальше )
- комментировать
- Комментарии ( 2 )
Алготрейдинг. Робот-кусака на РТС. Ri long and short.
- 08 марта 2016, 07:55
- |
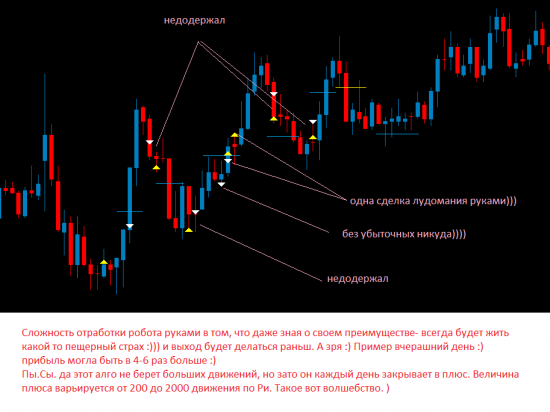
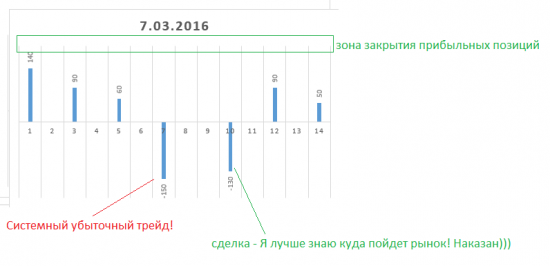
Распределение в Ри по сделкам.
Начало нового цикла! USD/RUB (W/D/H)
- 28 февраля 2016, 13:23
- |
Динамика USD/RUB в начале марта может изменить свое среднесрочное направление. Многолетние наблюдения за данным торговым инструментом дают возможность подтвердить повторяющееся явление, которое регулярно происходит вначале марта.
Также в это время меняют свою динамику и фондовые индексы. Американский рынок становится более привлекателен для инвесторов, сразу можно будет сделать вывод о том, какие акции в феврале-марте окажутся сильнее рынка, такие и стоит приобретать в свои инвестиционные портфели.
Традиционно в марте появляется спрос на металлы, нефть и другие ресурсы. Во второй половине февраля заканчиваются длинные каникулы в Китае (второй по силе экономике мира после США), тем самым ознаменуется начало нового экономического цикла в целом для мировой экономики.
Доллар традиционно слаб в марте против многих валют мира, в том числе и против рубля. Как правило это явление более отчетливо видно не сразу с самого начала марта, а после 5 марта.
( Читать дальше )
евро
- 03 февраля 2016, 16:27
- |
Вот евро например — оно растёт,
Шортить его — что ссать в свой огород.
Дождись консолидации сначала,
Потом подумаешь...,
А может стоит прикупить, его сначала?
Значение торгового алгоритма в торговле.
- 03 февраля 2016, 13:42
- |
Добрый день, дорогие друзья.
Буквально не так давно, мы с Вами обсуждали важность и наличие торгового алгоритма в нашей с Вами торговле.
Алгоритм — это набор инструкций, описывающих порядок Ваших действий для достижения результата.
Его задача заключается в том, чтобы помочь систематизировать торговлю и выработать подходящую стратегию для получения положительного результата.
С моим коллегой, мы решили сделать упор на создание торговый правил каждым участником торгов и провели вебинар на эту тему.
Также мы решили не нагружать Вас и разбили его на 3 части для легкости просмотра.
Уверен, многим из Вас, информация будет полезна, а также будет макетом в создании то самой бумажки, которой так не хватает во время торгов.
Огромной всем удачи и приятного просмотра.
USDRUB Weekly/30m
- 21 января 2016, 18:08
- |
Приветствую всех участников!
USDRUB
Таймфрейм Weekly
Используя в работе шаблон: smart-lab.ru/blog/188078.php приходишь к следующим выводам: покупка, открытая (7.12.2015-11.12.2015), также возможно открытая ранее или позднее данного периода времени пока еще может быть открыта, явных сигналов на данном таймфрейме для закрытия позиции нет!
Ранее была дана рекомендация: «Держать покупку пока цена будет выше 67.863(по данному графику), при закрытии ниже данного уровня переход в противоположную сделку».
Таймфрейм 30m
Используя в работе шаблон: smart-lab.ru/blog/188078.php приходишь к следующим выводам: ключевая отметка (уровень активации сделки) — 84,195.
Рекомендация следующая: Таймфрейм 30m
В случае закрепления цены выше данной ключевой отметки 84,195 — покупка и ожидание продолжения ралли.
В случае закрытия ценой на данном таймфрейме ниже 83,753 (уровень реверс) после момента активации на отметке 84,195 — продажа. (для продавцов сигнал для открытия позиций на понижение по данному торговому инструменту на данном таймфрейме, с возможным повторением сигнала согласно фрактальной системе).
( Читать дальше )
Вебинар с Александром Литвиненко и Романом Шкудором - 10 Элементов торговой стратегии
- 25 декабря 2015, 19:37
- |
Выкладываем запись вчерашнего вебинара, приятного просмотра.
Всем хороших выходных!
Полуграаль в одной картинке с iPad'a.
- 23 декабря 2015, 03:34
- |
Собственно, это, скорее всего, мои же пояснения к другой картинке,
вот этой: http://smart-lab.ru/blog/268751.php
USDRUB, Weekly
- 13 декабря 2015, 13:13
- |
USDRUB
Используя в работе шаблон: smart-lab.ru/blog/188078.php приходишь к следующим выводам: покупка на текущей неделе с (7.12.2015-11.12.2015). Держать покупку пока цена будет выше 67.863(по данному графику), при закрытии ниже данного уровня переход в противоположную сделку.
Всем удачных инвестиций!

- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал