Рецензия на обобщенную модель ценообразования опционов Виталия Курбаковского

Волею судеб прочитал статью Виталия Курбаковского, где он предлагает свою модель ценообразования опционов. Ссылка https://smart-lab.ru/blog/135564.php . Статья интереснейшая, демонстрирует высокий уровень как практической так и теоретической подготовки автора, отличную интуицию и методологию научного поиска. Прочитал и изучаю с удовольствием! Рекомендую всем, кто работает с опционами, да и не с опционами тоже. Очень жалею, что не прочитал раньше. Даже небольшую рецензию сподвигся написать :)

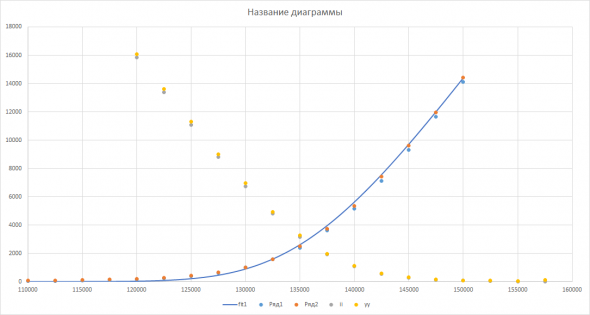
Как-то так получилось, что наверное любой опционщик знаком со словами типа “улыбка волатильности”, “подразумеваемая волатильность” итд. История возникновения этих слов имхо проста и эволюционна. Блэк и Шоулс написали свою теорию, в которой в числе прочих была буква сигма--просто константа теории, которую они назвали волатильностью. Вскоре выяснилось, что теория неверно описывает реальные рынки и невозможно удовлетворительно зафиттировать реальные цены опционов, манипулируя только константой сигма. Как пример--попытка фиттирования формулой Блэка и Шоулса опционов на фьючерс РТС, дата 21.06.2019, экспирация 18.07.2019, время до экспирации 27.3 дня, ЦБА=135700:

Точки--это аски и биды реальных цен, сплошная кривая--фиттирование реальных цен формулой БШ с волатильностью как параметром. Ну вот не очень. Качественно неплохо, а количественно как-то не особо. И не сделаешь ничего.    

Ну неправильная теория (правильная с какой-то точностью, правильнее сказать :) ), это бывает, сплошь и рядом. Что же делать? И вот тут, на мой взгляд, произошло движение по наипростейшему пути, что так часто бывает в эволюции. Одной из черт реальных рынков является дискретность по страйку. То есть страйков конечное число, точечек на этой кривой конечное число. А кроме того, зависимость цены опциона по БШ от волатильности является гладкой взаимно однозначной функцией--так уж оно устроено, да и не может быть по другому, ибо чем больше неопределенность, тем выше цена страховки от нее, то есть цена опциона. В этих условиях прямо и подмывает каждой точечке назначить свою волатильность. Ибо волатильности эти будут примерно равны, поскольку кривулька на картинке выше более или менее вблизи точек проходит. Собственно, так и поступили. Каждой точке назначили свою волатильность, назвали ее IV--implied volatility. Дальше стали строить через точки на зависимости IV от страйка аппроксимирующие кривые, назвали их улыбкой/ухмылкой/прямой/кривой волатильности. Вот такая история, неплохая в общем-то--но надо понимать, что это просто костыль под теорию БШ и не более.

Естественно, концепция переменной IV в зависимости от страйка делает теорию БШ внутренне противоречивой. Изначально в теории БШ уравнение Ито и следующее из него уравнение на равенство нулю случайной части безрискового портфеля решаются в приближении постоянной волатильности, никаких зависимостей от страйка или чего-то еще там нет. А все слова про IV--это просто костыли для приматывания БШ к реальным ценам.  

Тогда возникает вопрос--а нет ли лучших костылей, ибо умничать с этими улыбками/ухмылками, аппроксимировать их полиномами/арктангенсами--это как-то надуманно все. Вопрос этот многогранный, много различных вариантов предложено. Автор, на мой взгляд, предложил отличный вариант с точки зрения практика на бирже. Просто изумительный, на мой взгляд, сейчас вот изучаю и радуюсь. При этом степень издевательства над строгостью в теории БШ формально равна степени издевательства над строгостью при применении концепции кривой волатильности--то есть считаются переменными те параметры, которые в теории постоянны. Но, на мой взгляд, предложенные автором параметры гораздо более понятны и удобны, а кроме того--их меньше.  

Итак, что предлагается. Коэффициент перед Винеровским процессом в уравнении Ито, описывающем ЦБА, в теории БШ пропорционален ЦБА. Это соответствует логнормальному процессу. Автор говорит--а давайте возьмем не простую пропорциональность, а линейную зависимость. То есть не b*F, а a+b*F, где F--это ЦБА. Что здесь хорошо? Что можно решить диффузионное уравнение для цены опциона точно так же, как это сделали Блэк и Шоулс, через формулу Пуассона для краевой задачи. Просто делаем замену a+bF=m и все, дальше все абсолютно так же. В итоге получатся те же формулы для цен опционов, только они выражены через m и b, а не через a,b и F. А вот дальше автор говорит следующее. Давайте полагать m некой константой. Разумеется, это делает теорию внутренне противоречивой, равно как введение переменной IV делает внутренне противоречивой оригинальную теорию БШ. Но. Имхо, если подумать, то автор ведь имеет на то гораздо больше оснований, чем создатели IV. Ведь m--это просто коэффициент перед Винеровской частью в уравнении Ито. И да, локально можно считать его постоянным, при этом понятна ошибка и понятно, когда это приближение неверно. А также ясен физический смысл величины m--это просто изменчивость базового актива, таким образом, можно будет сопоставлять m, полученное из фиттирования цен опционов и m, находимое из динамики базового актива (что автор и делает в конце статьи).

Имея все это в голове, как минимум интригует проверка качества фиттирования реальных цен опционов (см. график выше) формулами БШ с параметрами m и b. При этом весьма красиво выглядит то, что m напрямую связано с ценой опциона со страйком, равным ЦБА, откуда появляется возможность легко оценить m через ординату точки пересечения кривых пут и колл. Это очень красивая возможность, позволяющая свести двухпараметрическое фиттирование по m и b к однопараметрическому, по b. Ну и производя фит по b (автор делал это методом МНК, я пока просто на глазок) выявляется картина отличного качества фита:

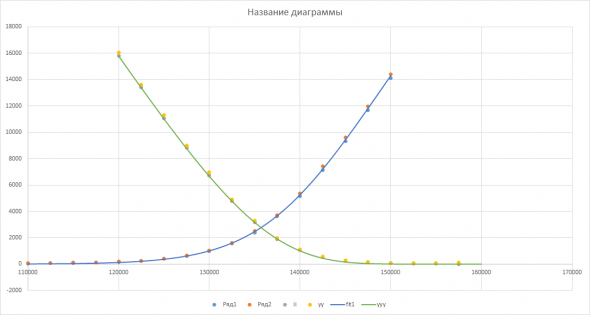
Здесь m=25500, b_Put=-0.9, b_Call=-0.7. Это однозначно выглядит гораздо лучше, чем фиттирование сигмой из классической теории БШ. И если увеличить детализацию картинки--то имхо не хуже, чем фиттирование при помощи IV, только параметров всего три и нет никакой мути типа шестипараметрической кривой с подгонкой асимметрии и эксцесса гауссом и арктангенсом как в теорцене биржи. 

Таким образом, есть весьма вероятное предположение (аккуратно пишу, потому что мало еще кейсов посмотрел, для уверенности надо больше. Ну и хочется скормить модели не только простые случаи типа РТС, но и что-нибудь похитрее типа опционов на VIX), что автором предложена простая и физичная модель ценообразования опционов, требующая гораздо меньше искусственности, чем широко применяемая модель зависимости IV от страйка. Автору огромная благодарность и уважение за научную интуицию и труд, отличная работа!