SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Kot_Begemot
Контроль рисков в играх с рекапитализацией
- 04 ноября 2019, 20:28
- |
Сложность задачи контроля рисков состоит в том, что риски в действительности не ограничены и нарастают с течением времени так, что превращают бесконечно длительные игры с полной рекапитализацией в игры с абсолютно неконтролируемым риском. В связи с чем, задача выбора оптимального плеча (объёма) становится в общем случае математически не решаемой, а риск-менеджмент, в конечном счете, определяется только психологическим комфортом управляющего или инвестора. Тем не менее, исходя из некоторых предпосылок мы можем ограничить зону допустимого психологического комфорта и склонности к риску, то есть указать на некоторые их разумные пределы.
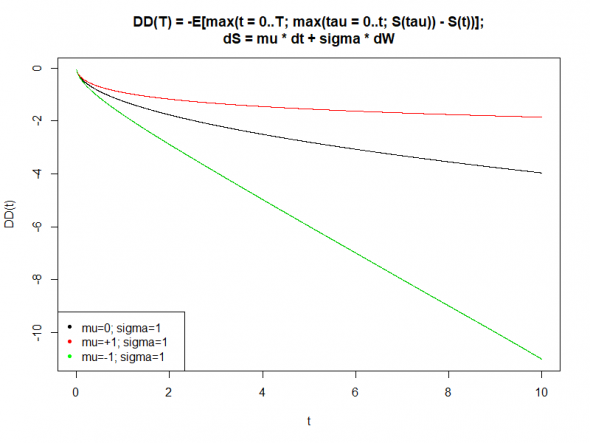
Изображение зависимости средней ожидаемой максимальной просадки заданных стратегий от времени. Любезно позаимствовано у Eugene Logunov.
Как и ранее, имея стартовый капитал 50 млн. долларов США мы будем пытаться обыграть господина Баффета, имеющего 500 млрд. долларов США, то есть будем стараться увеличить свой капитал в 10 000 раз за счёт игры на бирже. Играть мы будем нелинейно, то есть будем увеличивать ставки после каждого удвоения пропорционально текущему капиталу и поэтому для реализации нашей цели нам предстоит выиграть у господина Баффета не 10 000 раз подряд, а всего лишь:
Мы знаем, что наша стратегия обладает преимуществом над стратегией господина Баффета и позволяет играть против него с вероятностью 55%/45%, то есть с 10% смещением (Шарп = 1.6)
Нам так же известно, что уменьшая «плечо» и сокращая доходность, общая вероятность победы в серии испытаний (вероятность удвоения капитала) растёт пропорционально:
где n — необходимое число последовательных выигрышей для удвоения капитала, а 1/n — риск (волатильность) на сделку.
В этом случае вероятность закончить полную игру с положительным результатом, то есть, непосредственно разбогатеть, а не потерять, пропорциональна:
Рассмотрим поведение этих величин графически:
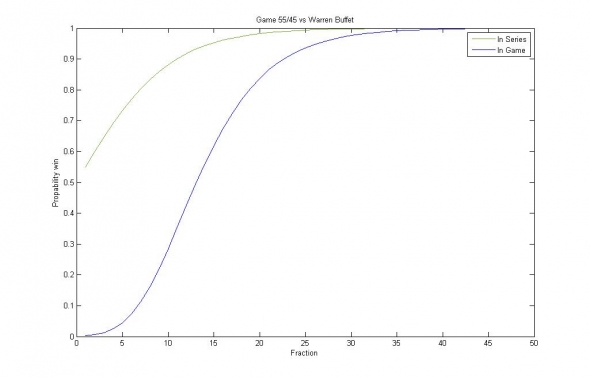
Изображение — вероятность увеличения капитала на 1млн.% (синяя линия), и вероятность удвоения капитала (зелёная линия) при дроблении капитала на n частей, отложенных по оси абсцисс для стратегии, обладающей годовым Шарпом 1.6.
Видно, что для стратегии данного качества (Шарп = 1.6), ограничение годовой доходности должно составлять около 60% годовых (риск = 1/40= 2.5%), а ограничение 3 сигма просадки на уровне 50%. В этом случае мы можем быть почти уверенными (>99.5%) в том, что стратегия не разорит нас на дистанции 1 млн. процентов. При ограничении 3-сигма просадки в 80%, доходности 75%, а ставки — 1/30 - мы будем увеличивать свой капитал на 1 млн.% только в 92% случаев.
Аналогично и для стратегий более низкого качества - требования к рекапитализации удовлетворяются при схожих ограничениях квантильных просадок на уровнях 20-25% (2 сигма) и 45-50% (3 сигма). Для показателя Шарпа 1, например, это соответствует риску 1/75 = 1.3% на сделку и ограничению доходности на уровне 20% годовых.
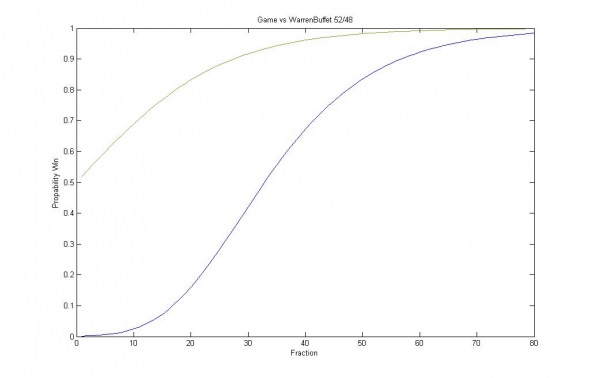
Изображение — вероятность увеличения капитала на 1млн.% (синяя линия), и вероятность удвоения капитала (зелёная линия) при дроблении капитала на n частей для стратегии, обладающей годовым Шарпом 0.6.
* Ограничение данной модели — полное отсутствие зачатков интеллекта у господина Баффета и стационарность среднего независимых испытаний, а не среднего независимых серий испытаний.
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика



















Опечатку поправил.
Предположим, у меня есть стратегия. Честный бэктест говорит, что за 10 лет шарп 2. С каким плечом её можно торговать? Мы же знаем, что рынок меняется. Или не меняется, но, в силу длительности фаз рынка, могут быть периоды с гораздо большим и гораздо меньшим шарпом ДЛЯ ТОЙ ЖЕ САМОЙ СТРАТЕГИИ. Короче, все критерии Келли полуКелли и четвертьКелли для наших задач есть сферический конь в вакууме.
Должен предупредить также, что простые методы формирования портфеля типа марковица работают плохо, если вообще работают. Как метод первого выбора, я предпочитаю просто уравнивать амплитуду рисков компонент. И, конечно, нужен учет взаимозависимости систем. В общем, задача содержательная.
Может быть я и не прав, но с этим делом нужно быть осторожнее — моделировать просадки по Монте-Карло или считать их теоретические распределения.
Есть страты у которых на недельках даже шарп «будет трёхзначный», но внутри дня может твориться дичь + потолок ликвидности достигается за 3 удачных года подряд со стартовой в лям рублей.
Берёшь в голову малое, а оно вдруг становится большим — ну вы, девушки, знаете, такое бывает ;)
А за топик автору огромное спасибо!
Но, гипотеза эффективного рынка предполагает, что у господина Баффета нет мозгов или, если есть, то настолько дезорганизованные, что поднять на маленького котёнка руку они попросту не в состоянии.
Eugene Logunov, если вы имеете ввиду вот это . То это наивернейший путь к сливу.
Взяв, например, игру 60/40, +1/-1, ставка составит 20%.
Синяя — счёт, зелёная — текущая просадка в долях от капитала (правая ось)
В этих условиях можно поставить ставку 100 Келли и тоже получить просадку не более 100%, правда график никуда не взлетит, но это уже дело десятое.
Если вы отчаянный скальпер, то можно, наверное, использовать критерий Келли/2-3-4 (чтобы вылезти из ямы нелинейности), но если вы встаёте в тренд, а он вас сажает на 10-20-30-40-50%% без изменения ставки, то лог-масштаб становится уже не применим.
Принципиально, конечно, даже если продать Сбербанк на минимумах, потом купить на максимумах и повторять эту процедуру до бесконечности, то от депозита всё равно что-то, да останется — это я понимаю. А по моим методикам просадка улетит куда-то в область минус бесконечности...
Такая вот котовасия с этой нелинейностью
Взял 4 Келли и получил скатывание ровно в ноль с последующей болтанкой в районе управляемого капитала 0.0000001 цента.
Интересный график получился. Но что-то считать просадки в лог-масштабе у меня не возникло никакого желания. Даже если бы я корректировал позицию каждый день (пирамидил и резал), а не переносил бы полным объёмом через ночь. Потому что это всё «краевые» эффекты бесконечностей. Логарифм от 50% просадки и будет 50% просадка (примерно), а от минус бесконечности — только 100%. Здесь разница в том, что вы пытаетесь «играть» на асимметрии лог масштаба, а я — нет, вы работаете в зоне крайней неустойчивости (нелинейности), а я — нет. Поэтому работаю в аддитивном масштабе.
А как у вас минус может даже теоретически получиться я не понимаю. Понимаю, когда капитал меньше минимального лота и брокер требует довнести деньги, а как в минус уйти — нет. Потому что чтобы уйти в минус нужно взять ставку больше 5 келли и стартуя с 1 получить, скажем 1*(1-1.2) = — 20% от счёта. А до ставок в 5 келли в минус уйти не возможно.