SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. 3Qu
Совершенствуем Exponential Moving Average (EMA).
- 16 января 2021, 00:04
- |
На днях написал топик с описанием своей старой стратегии - Ретростратегия ретро ТС., снятой с эксплуатации в далеком 2014 г, которая, как оказалось, даже в упрощенном виде может работать и сегодня. Не собирался ее использовать, но в ходе обсуждений решил потратить на нее пару вечеров, восстановить по памяти до последней ее версии, и посмотреть, не стоит ли отложить текущие дела, и быстренько вывести ее на рынок.
В ходе восстановления пришлось также дорабатывать фильтры ФНЧ, простейшим из которых является ЕМА. Я дорабатывал свои фильтры, а вам покажу, что можно сделать с ЕМА, чтобы ее усовершенствовать и улучшить.
В комментариях к топику о ретростратегии упомянули некоего Jurik (jurikres.com) и его JMA. Думал, что он уже забыт, но, жив — курилка. То, что мы получим будет не хуже его индикаторов и подобрав периоды сглаживания можете сами в этом убедиться. Вообще, все поделки Jurikа — это где-то на уровне лабораторных работ студентов 4-го курса института по курсу ТАУиР. Наши сегодняшние тоже сложностью не отличаются, но может даже лучше, хотя бы потому, что не являются черными ящиками, и вы знаете как это устроено.
Выражение для ЕМА знают, пожалуй, все:
Y(t) = a0*X(t) +b1*Y(t-1).
У нее много недостатков, одним из которых является большая групповая задержка. Попробуем исправить это, и для начала вычислим ошибку слежения ЕМА за котировками:
delta = x(t) — Y(t-1).
Теперь добавим эту ошибку с некоторым коэффициентом Kos к X(t) (это называется — обратная связь), и получим выражение для нашей скорректированной ЕМА:
Y(t) = a0*(X(t) + Kos*delta) +b1*Y(t-1).
Теоретически Kos может принимать значения от 0 до 1, но увлекаться не надо, обычно достаточно Kos от 0 до 0.3.
Все, можете смотреть что получится.
В рассмотренном выше случае мы использовали так называемую линейную обратную связь, когда корректирующий сигнал пропорционален сигналу ошибки. Далее мы рассмотрим нелинейную связь, когда и сам коэффициент Kos меняется пропорционально ошибке. Запишем это:
delta_nl = Knl*abs(delta/y[t-1])*delta.
Здесь delta/y[t-1] сделано для того, чтобы delta_nl не изменялась от уровня цены, а зависела только от ее изменения.
В итоге, для нашей ЕМА с нелинейной обратной связью окончательно получим:
Y(t) = a0*(X(t)+ delta_nl) +b1*Y(t-1).
С Knl тоже увлекаться не надо, но он здесь достаточно велик, у меня Knl= 1.0.
Теперь можем скомбинировать обе обратных связи в одном индикаторе:
Y(t) = a0*(X(t)+ Kos*delta + delta_nl) +b1*Y(t-1).
И наконец графики того, что у нас из этого получилось на единичном скачке 1(t) — это такой стандартный тест для всяческих подобных систем, по которому, глаз пристрелямши, можно оценивать характеристики системы.
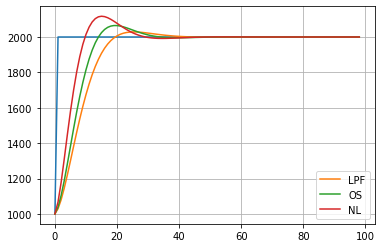
LPF — типовой ФНЧ фильтр,
OS — ФНЧ с обратной связью
NL — ФНЧ с комбинированной связью (последний вариант в топике)
Смотрим выбросы — 10% — это оч небольшой выброс, реально, если и будет виден, то только на гэпах.
Теперь посмотрим те же самые индикаторы на реальных котировках фьючерса Si.

На графиках все так называемы периоды сглаживания одинаковы. Я выбирал значения Kos и Knl такими, которые оптимальны для моих целей. Для ваших применений значения Kos и Knl могут быть совсем другими, и, соответственно, и графики будут иметь несколько иной вид.
Сорри, но для тестов я использовал не ЕМА, а свои ФНЧ, но на ЕМА тоже должно получится, когда-то давно я пробовал.
Вот и все.
Удачи.
В ходе восстановления пришлось также дорабатывать фильтры ФНЧ, простейшим из которых является ЕМА. Я дорабатывал свои фильтры, а вам покажу, что можно сделать с ЕМА, чтобы ее усовершенствовать и улучшить.
В комментариях к топику о ретростратегии упомянули некоего Jurik (jurikres.com) и его JMA. Думал, что он уже забыт, но, жив — курилка. То, что мы получим будет не хуже его индикаторов и подобрав периоды сглаживания можете сами в этом убедиться. Вообще, все поделки Jurikа — это где-то на уровне лабораторных работ студентов 4-го курса института по курсу ТАУиР. Наши сегодняшние тоже сложностью не отличаются, но может даже лучше, хотя бы потому, что не являются черными ящиками, и вы знаете как это устроено.
Выражение для ЕМА знают, пожалуй, все:
Y(t) = a0*X(t) +b1*Y(t-1).
У нее много недостатков, одним из которых является большая групповая задержка. Попробуем исправить это, и для начала вычислим ошибку слежения ЕМА за котировками:
delta = x(t) — Y(t-1).
Теперь добавим эту ошибку с некоторым коэффициентом Kos к X(t) (это называется — обратная связь), и получим выражение для нашей скорректированной ЕМА:
Y(t) = a0*(X(t) + Kos*delta) +b1*Y(t-1).
Теоретически Kos может принимать значения от 0 до 1, но увлекаться не надо, обычно достаточно Kos от 0 до 0.3.
Все, можете смотреть что получится.
В рассмотренном выше случае мы использовали так называемую линейную обратную связь, когда корректирующий сигнал пропорционален сигналу ошибки. Далее мы рассмотрим нелинейную связь, когда и сам коэффициент Kos меняется пропорционально ошибке. Запишем это:
delta_nl = Knl*abs(delta/y[t-1])*delta.
Здесь delta/y[t-1] сделано для того, чтобы delta_nl не изменялась от уровня цены, а зависела только от ее изменения.
В итоге, для нашей ЕМА с нелинейной обратной связью окончательно получим:
Y(t) = a0*(X(t)+ delta_nl) +b1*Y(t-1).
С Knl тоже увлекаться не надо, но он здесь достаточно велик, у меня Knl= 1.0.
Теперь можем скомбинировать обе обратных связи в одном индикаторе:
Y(t) = a0*(X(t)+ Kos*delta + delta_nl) +b1*Y(t-1).
И наконец графики того, что у нас из этого получилось на единичном скачке 1(t) — это такой стандартный тест для всяческих подобных систем, по которому, глаз пристрелямши, можно оценивать характеристики системы.

LPF — типовой ФНЧ фильтр,
OS — ФНЧ с обратной связью
NL — ФНЧ с комбинированной связью (последний вариант в топике)
Смотрим выбросы — 10% — это оч небольшой выброс, реально, если и будет виден, то только на гэпах.
Теперь посмотрим те же самые индикаторы на реальных котировках фьючерса Si.

На графиках все так называемы периоды сглаживания одинаковы. Я выбирал значения Kos и Knl такими, которые оптимальны для моих целей. Для ваших применений значения Kos и Knl могут быть совсем другими, и, соответственно, и графики будут иметь несколько иной вид.
Сорри, но для тестов я использовал не ЕМА, а свои ФНЧ, но на ЕМА тоже должно получится, когда-то давно я пробовал.
Вот и все.
Удачи.
теги блога 3Qu
- Binance
- C#
- C++
- DDE
- DLL
- EMA
- Excel
- Exponential Moving Average
- Lua
- machine learning
- metatrader5
- ML
- MOEX
- Moving Average
- Python
- QLua
- Quik
- Quik Lua
- Si
- Smart-lab
- SQLite
- автоматическая торговая система
- акции
- алготрейдинг
- базы данных
- Баффет
- биржа
- Боллинджер
- Брокер
- брокеры
- вероятность
- выбор
- Газпром
- дельта
- доллар
- Доллар рубль
- доска опционов
- идеология
- инвестиции
- индикатор
- индикаторы
- интрадей
- календарный спред
- календарный спрэд
- Кризис
- криптовалюта
- МА
- Машинное обучение
- моделирование
- модель
- нейросети
- нейросеть
- нефть
- опрос
- опционные стратегии
- опционы
- оффтоп
- плечо
- прогнозирование
- программирование
- психология
- реклама
- роботы
- рынок
- сеточник
- скальпинг
- скользящие средние
- случайное блуждание
- спекуляции
- спекуляция
- статистика
- стационарность
- стоп
- стопы
- Стратегии
- стратегия
- стрэддл
- стрэнгл
- Тейк
- терминал
- тест
- тестер стратегий
- тестирование
- технический анализ
- торговая система
- торговая стратегия
- торговые роботы
- торговые системы
- торговые стратегии
- торговый софт
- трейдинг
- ТС
- фильтр
- Фильтры
- Форекс
- фундаментальный анализ
- фьючерс
- фьючерс ртс
- фьючерсы
- эффективный рынок



















Кстати люблю аллигаторы Билла.На дневном они стирают влияние новостей и это очень полезно.
->
Y(t) = a0*(X(t)) +b1*Y(t-1) + a0*Kos*delta
где a0*Kos*delta
delta = x(t) — Y(t-1).
Y(t) = a0*(X(t) + x(t) — Y(t-1).) +b1*Y(t-1).
Y(t) = a0*(2*X(t)) — a0*Y(t-1) +b1*Y(t-1).
где b1= 100-a0
Y(t) = a0*(2*X(t)) — a0*Y(t-1) +(100-a0)*Y(t-1).
Y(t) = a0*(2*X(t)) + ((100)-(2*a0))*Y(t-1).
Y(t) = 2*(a0*(X(t)) + ((50)-(a0))*Y(t-1))
У тебя будет на простой линии ГОРИЗОНТАЛЬНО график выше всегда.
за счет коэффициента 2.
EMA = (CLOSE (i) * P) + (EMA (i — 1) * (100 — P), где:
CLOSE (i) — показатель цены закрытия периода,
EMA (i — 1) — значение скользящего среднего предыдущего периода,
P — доля использования значения цены.
а у тебя уже функция ema' от нее не будет равна 0.
цена это не линия.
а точки(сделки) с разрывами! между ними.
либо точки закрытия периодов.
а значит производную от цены, как есть, не взять.
а только из АППРОКСИМИРУЮЩЕЙ функции.
А производная от Аппроксимации например из n точек степени n будет гарантированно функция со степенью n-1 c другими коэффициентами.
В первую очередь производная опишет качество аппроксимации.
А не качество линии.
Честная производная от цены будет не определена.
Там везде разрывы во всех точках.
при z=a*(1+k)
y(+1) = z*x+(1-z)*y
легко видеть, что это уравнение EWMA c коэффициентом а+аk, то есть с меньшим периодом и меньшей памятью. Если k=0.3, то это равносильно уменьшению периода на 30%.
Опираясь на чутье…
Классически подразумевается, что коэффициенты (в вашей формуле a0 и b1) связаны соотношением: b1 = 1 — a0.
И если вы хотите сделать обратную связь в формуле, то константу delta корректнее записать так (в ваших обозначениях):
delta = x(t-1) — Y(t-1)
( у вас в формуле стоит x(t) )
ema
и
ema'
и дельту из ema!!! запихивает в ema'
народ, в основном, не понимает.
тут 90% народу sma формулу не вспомнят.
Речь шла о примере применении линейной и нелинейной обратной связи. В данном случае к ЕМА.
http://www.jurikres.com/catalog1/ms_ama.htm#top