Блог им. AGorchakov
О распределении приращений логарифмов H+L дней («давно я не брал в руки шашек»)
- 28 мая 2021, 20:29
- |
Это исследование я сделал под влиянием бурной дискуссии на форуме о распределении «хвостов» приращений логарифмов цен, возникшей, казалось, на «пустом месте»: насколько корректны доверительные интервалы для оценок параметров линейной регрессии в альфа-бета модели?
Кроме указанной ссылки, дискуссия продолжилась в еще двух ветках: тут и тут.
Действительно, эти оценки в классическом случае строятся на основе центральной предельной теоремы для статистик оценок параметров линейной регрессии. Однако, как я уже писал на смартлабе, необходимым условием которой является скорость роста дисперсии суммы слагаемых как О(N), N – число слагаемых, а для быстрой сходимости в центральной области еще и требуется конечность абсолютного третьего момента любого слагаемого (если говорить о сходимости на всей прямой, включая «большие уклонения», то еще требуется и конечность всех моментов отдельных слагаемых). Однако эти условия не выполняются для части распределений Парето и Стьюдента с полиномиальной скоростью убывания «хвостов» и поэтому для «хорошего» приближения суммы таких слагаемых нормальным законом требуется очень большое число испытаний, которых, как правило, в альфа-бета модели, построенной на дневных данных, нет. А значит традиционные методы построения доверительных интервалов для оценок параметров этой модели «не работают».
Собственно дискуссия в дальнейшем свелась к вопросу: распределены ли «хвосты» дневных приращений логарифмов цен по распределению Парето, т. е. c полиноминальным убыванием О(х-а) или мы имеем дело с экспоненциальным убыванием вида О(e-axxb), а>0, b-любое.
Первый результат основан на выделении отдельно «хвостов» и их приближении распределением Парето. При этом центральная область игнорируется, так как приблизить все распределение приращений логарифмов цен распределением Парето никак не получается. А что говорит в пользу второй гипотезы?
В своем видео с 21-й по 32-ю минуту я привожу рассуждения, на основании которых для приращений логарифмов H+L (ht) дней будет иметь место распределение
со скоростью убывания «хвостов» О(e-axx-1/2), K0-функция Макдональда.
Там же показана графическая «похожесть» этого распределения на распределение приращений логарифмов H+L фьючерса на индекс РТС в 2005-2016 годах с выброшенным периодом «кризиса» с 17 сентября 2008-го по 28 февраля 2009-го. Однако никаких результатов статистических исследований не приведено. Восполним данный пробел на примере SPY на данных с 29.01.1993 по 24.05.2021.
Прежде чем переходить к результатам поясним, что из себя представляют приращения логарифмов H+L. В начале 2000-х я выяснил, что для РАО ЕЭС и Газпрома они имеют корреляцию больше 0,99 с приращениями логарифмов средневзвешенных цен дневок. Т. е. мы имеем дело с рядом приращений логарифмов средневзвешенных цен дневок, которые, ИМХО, более точно отражают картину дневных настроений, чем цены закрытия, т. е. цены в отдельный момент дня. А почему SPY, а не S&P500, история которого гораздо длиннее? Все дело в том, что в данных индекса не учитываются междневные гэпы из-за равенства открытие сегодня=закрытию вчера. И при наличии гэпа мы получаем, что в H или L могут присутствовать цены, которых вообще не было на торгах.
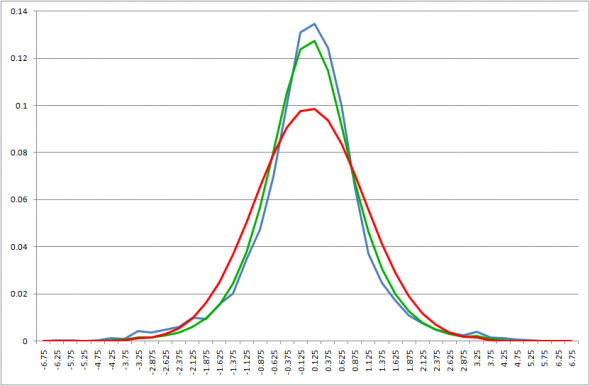
Возьмем весь ряд дневных приращений логарифмов и приблизим указанным распределением. Для плотностей получаем следующую картинку
Здесь и далее на графиках синим цветом обозначена гистограмма вероятностей распределения приращений логарифмов цен, нормированных среднеквадратичным отклонением, зеленым – аналогичная наиболее «близкая» гистограмма, для распределения с вышеприведенной плотностью (обозначим ее Kо по аналогии с функцией Макдональда), а красным – та же гистограмма для нормального распределения с таким же средним, как у нормированных приращений логарифмов цен и дисперсией 1 (напомним, что дисперсия нормированного ряда приращений логарифмов тоже равна 1). Из этих гистограмм вероятностей получают функции распределения для сравнения по критерию Колмогорова.
Несмотря на визуальную «близость» зеленого и синего графика значение статистики Колмогорова отвергает гипотезу совпадения распределений с вероятностью ошибки первого рода 0.05 (см. сводную таблицу ниже: критическое значение статистики для вероятности ошибки первого рода 0.05 – 1.36). Итак, на всей истории получить приближение указанным распределением не удалось. Впрочем, и в вышеупомянутом видео я выбрасывал значения выборки для кризисного периода с 17 сентября 2008-го по 28 февраля 2009-го, специально оговорив, что в этот период, вероятней всего, данное распределение далеко от реальности.
А давайте по аналогии с факторным анализом из видео разобьем весь период на кластеры «волатильности» и посмотрим, что получается отдельно на каждом из кластеров.
Под текущей «волатильностью», как и в случае факторного анализа, мы будем понимать максимум из двух величин:
— оценка сигма из упомянутого распределения по приращениям логарифмов H+L за 50 последних дней (меньше нельзя из-за ошибки оценки), т. е. в предположении, что параметры этого распределения были постоянны в эти 50 дней;
— СКО тех же приращений логарифмов за последние 10 дней.
Почему так? Вторая оценка очень неточная, но она позволяет быстро среагировать на рост волатильности. В то время как первая «увидит» реальный рост только примерно через 25 торговых дней в силу сдвига «окна» расчета. Основной ошибкой такого расчета является то, что однодневный всплеск приращения логарифма можно принять за новый кластер более высокой волатильности в течении 9 дней, пока этот однодневный всплеск не уйдет из расчета. Но с точки зрения рисков — эта ошибка менее критична, чем ошибка пропустить реальный рост волатильности, которая при таком подходе менее вероятна.
И, кстати, для достаточно сильно разнесенных отрезков времени оценки сигма могут сильно отличаться, что свидетельствует о том, что этот параметр нестационарен. Однако больших «ступенек» (больше 25% от предыдущей величины) ни в одном из его выборочных рядов, разнесенных на 25 точек, нет. Что говорит об отсутствии больших «гэпов» (в разы) в этой величине и ее относительно «плавной» изменчивости. А это значит, что те же «хвосты» в исходной последовательности, либо серийны и появляются в результате постепенного нарастания «волатильности», либо единичны и крайне редки («черные лебеди»).
Вот какие у нас получились кластеры
О столбце «Без кризисов» чуть позже.
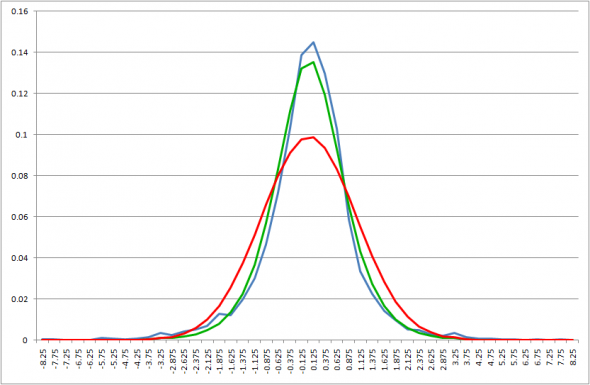
Начнем с кластера «низкой» волатильности
И мы сразу получаем по критерию Колмогорова, что гипотеза о совпадении распределений для нашего распределения не может быть отвергнута. Хотя гипотеза нормальности отвергается по этому критерию.
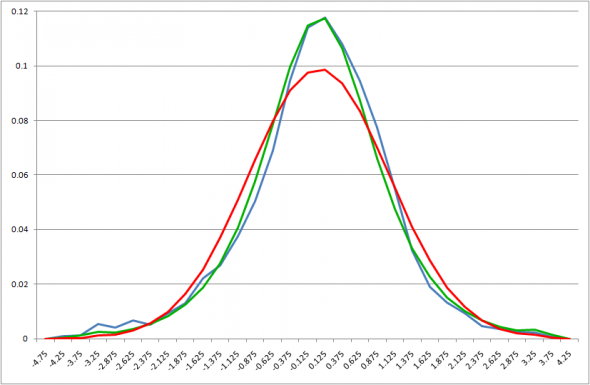
Еще лучше по тому же критерию получается для «средней» волатильности
Нормальное распределение, по прежнему, «вне игры».
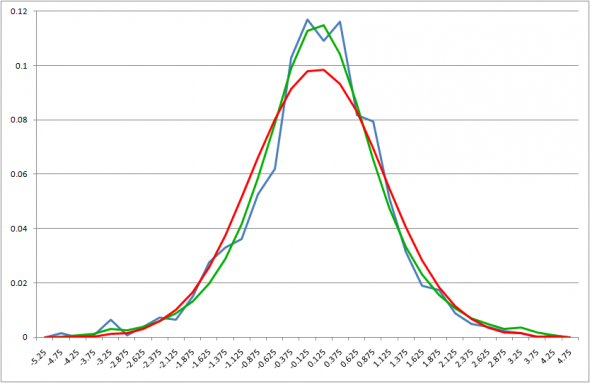
И для «высокой» «волатильности» критерий Колмогорова дает нам совпадение с нашим распределением
И даже совпадение с нормальным получается по этому критерию. Но надо учесть, что после нормировки мы получили совсем уж «вычурное» распределение, лежащее в диапазоне [-2,2] и всего из 42-х точек. Кстати, «вычурность» этого распределения косвенно свидетельствует о том, что «сверхтяжелые хвосты» являются порождением «волатильности» в нашем определении.
Также отметим, что из 42-х последних точек, 40 попали на периоды 17.09.2008-15.12.2008 и 24.02.2020-10.04.2020, т. е. на «острые фазы кризисов». Поэтому последним шагом выбросим из данных эти периоды и посмотрим что получилось «Без кризисов»
И даже для этой выборки критерий Колмогорова дает нам совпадение с распределением Kо, хотя и «на тоненького». Ну а нормальное по прежнему «вне игры». Сводные данные по значениям статистики Колмогорова приведены в следующей таблице
Отметим также явную зависимость значений статистики Колмогорова от размаха колебаний нашей «волатильности» на выбранном периоде, что говорит о том, что для периодов с меньшим размахом, вероятней всего, приближение выборочного распределения распределением Ко будет еще лучше.
Таким образом, высказанная в видео гипотеза о том, что приведенное распределение хорошо «объясняет» одномерное распределение приращений логарифмов цен Н+L дневок вне периодов «острых фаз кризисов» полностью подтвердилась на SPY.
теги блога А. Г.
- "пила"
- "русский Баффет"
- CNYRUB
- comon.ru
- IMOEX
- S&P500
- S&P500 фьючерс
- Si
- автоследование
- акции
- алгоритмическая система
- алгоритмическая торговля
- алгоритмический трейдинг
- алготрейдинг
- банки
- Баффет
- бесплатные вебинары
- бинарные опционы
- биткоин
- брокеры
- Веселье
- волатильность
- встреча smart-lab
- Газпром
- Горчаков
- Горчаков Александр
- денежная масса России
- денежно-кредитная политика
- дивиденды
- доверительное управление
- доллар
- Доллар рубль
- ДУ
- ИК ФОРУМ
- инвестиции
- Инвестиции в акции
- Индекс ММВБ
- индекс РТС
- Индекс МБ
- индекс ММВБ
- индекс Мосбиржи
- индекс РТС
- индексы
- инфляция в России
- итоги года
- итоги месяца
- Ключевая ставка ЦБ РФ
- контртренд
- Конференции смартлаба
- конференция смартлаба
- копилка
- коронавирус
- короновирус
- кризис
- криптовалюта
- ЛЧИ
- ЛЧИ 2019
- ЛЧИ 2021
- макроэкономика
- макроэкономика России
- мемуары
- Мосбиржа
- мошенники
- нерезиденты
- нефть
- Новый год
- облигации
- опрос
- опционы
- оффтоп
- РБК-ТВ
- риски
- российские акции
- Россия
- рубль
- Русский Баффет
- рынок
- рэнкинг мосбиржи
- рэнкинг управляющих ММВБ
- санкции
- Сбербанк
- сбой на бирже
- системная торговля
- системный трейдинг
- смартлаб
- ставка ЦБ
- США
- теория вероятностей
- торговые роботы
- трейдинг
- Уоррен Баффет
- усреднение
- философия трейдинга
- Финам
- Форекс
- ФРС
- фьючерс MIX
- фьючерс ртс
- ЦБ РФ
- экономика России




















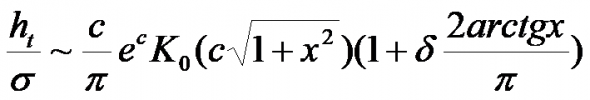



Просто хотелось бы знать математика, одобряет патерны или в контрах с ними? Расчеты-это долгий процесс, поэтому я выбрал такой подход, который можно на коленке состряпать за несколько минут, а эффект будет не хуже.
Но что самое интересное что не на каждом инструменте они отрабатываются на все 100%. И вот что я понял, на высоколиквидных и волотильных инструментах существуют так называемые «паттерны ловушки» с ложным выносом стопов и захватом ликвидности. Я называю это «загребать жар, чужими руками». Но ложные паттерны я использую для контр-трендовой стратегии. Вы спросите: а как я понимаю что паттерн ложный или нет? А вот для этого использую объемы, фьючерсные, опционные, ну и учитываю корреляцию взаимосвязанных инструментов. «Примаркет-закрытие» и отработка «фундаментала», до выхода новостей. Как бы много, много всего, но если разложить это по полочкам, в зоне доступа, то процесс занимает несколько минут. С учетом того что надо еще найти коридор банковского интереса и ММ, учитывая АТР.
Существует негласная поговорка: примаркет для «молодежи», закрытие для «старичков». Придерживаюсь такого же мнения.
Просто уверен, что не один спикер об этом не расскажет, а тем более не покажет наглядно. Вот даже Вы говорите что это все в рамках гипотезы и 50 на 50. А я считаю что это не так.
Так что столь глубокие исследования «распределений» были бы интересны для «внутри дня» на секундной-минутной дискретизации.
А что касается опционов, то я только в предыдущем своем посте писал, что эффективные стратегии на них могут быть основаны только на отличии реального распределения приращения цены (логарифма цены) до экспирации от того, которое «подразумевает» рынок «в моменте». Текущая «ухмылка волатильности» — это лишь «кривое зеркало» подразумеваемого рынком распределения, ничего не говорящая о реальном.
Правильно ли Вас понял, что Вы изучали следующие величины:
M[n] = (H[n]+L[n]) / 2
M[n-1] = (H[n-1]+L[n-1]) / 2
после чего переходили к нормированным приращениям их логарифмов
X[n] = LN( M[n]/M[n-1] ) / S[n]
где S[n] — оценка СКО величин X на момент n?
Которые и показали такое интересное распределение?
хороший, кстати, вопрос ....
пройтися S по всей выборке, чтобы иметь ориентировочное представление на предмет в будущем, что вот она появилася волатильность, выходящая за доверительный интервал…
И, кстати, там же даётся альтернативный эмпирический вариант «оценки» сигма, который очень прост.
Пара вопросов:
1) Каким критерием можно оценить правильность распределения, если количество данных 4000-5000?
2) каким критерием можно проверить, что у данных логнормальное распределение?
Альфа-бета простейшая модель, удобная для тех, кто анализирует индексные паевые фонды и тому подобная. Зачем её было замешивать с Парето, с хвостами распределений я так и не понял.
Что касается конкретно данной статьи.
Если мы исходим не из потребностей практики, а из чисто академического интереса, я бы попробовал (а) оценить волатильность для каждой точки по её центрированной выколотой окрестности (б) разделил каждое приращение на соотв. ему амплитудную оценку волы (в) вот это бы и аппроксимировал.
То есть, приращения с исключенной нестационарностью волы.
Там и весь спор то начался из-за того, что добавление в модель в качестве фактора модуля приращения логарифма при классическом расчете ничего не дало. Поэтому у автора модели возникли вопросы к ограничениям в классическом расчете модели линейной регрессии. Он настаивал на обязательности нормальности отдельных элементов выборки, я показывал, что достаточно ограниченности абсолютных третьих моментов. На что оппонент возражал, что для Парето условие ограниченности абсолютного третьего момента не выполнено. Так и возникла дискуссия: почему Парето и откуда оно взялось.
А в остальном Вы правы. Наверное корректнее брать в качестве оценки текущей «волатильности» интервал, где текущая точка — центральная. Просто с точки зрения практики — это «заглядывание в будущее», которого я хотел избежать даже в этом случае.
Я Вам написал на финамовскую почту, другой у меня нет.
Можно использовать например тест Anderson–Darling, он учитывает «масштаб», но он тоже свои сложности имеет, в хвосте мало данных и прыжки получаются.
r*X+(1-r)*У, где r случайная величина равная нулю или единице и р(r=1)~1, а Х и У — две разные случайные величины
вообще лучше всего критерий Манна-Уитни для понимания, какое распределение Х и какое р(r=1).
Ведь Парето на всем множестве приращений цен или логарифмов цен и быть не может.
А Колмогоров-Смирнов — самый хороший критерий только для случая выборки из одного и того же непрерывного распределения с плотностью и любыми ее «хвостами». Если функция распределения со скачками, то да, критерий Колмогорова-Смирнова «не очень», но судя по тому, что и у Anderson–Darling интеграл от Fn, то тоже для скачкообразных распределений «не очень».