SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. Lemmy
Как торговать стохастический диапазон
- 13 декабря 2012, 14:18
- |
Обычная картинка в арбитраже имеет примерно такой вид:
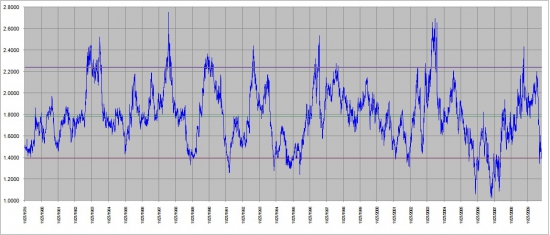
На каком тайм-фрейме – не принципиально. Она может быть как бесконечно устойчивой во времени, так и иметь локальный характер. Во втором случае арбитраж сводится к тому, чтобы нарезать в диапазонной торговле прибыли больше, чем потерять впоследствии на сдвиге диапазона или того хуже на трендовом выносе из него.
Так или иначе, пока стохастический диапазон держится, его можно контр-трендово работать.
Возникает вопрос об оптимальной стратегии такой контр-трендовой торговли.
Стандартный подход, используемый почти всеми арбитражерами, – пирамида сделок. Когда по мере отклонения от средней позиция наращивается с каким-то ценовым шагом. Обратное закрытие позиции может быть как таким же пошаговым, так и сразу всего объема в районе средней диапазона (назовем это статистическим нулем).
Смею утверждать, что это не самый оптимальный способ работы стохастического диапазона.
Представим весь диапазон в виде функции плотности распределения цены по ценовой шкале. Например, в случае вышепоказанного графика она будет иметь такой вид:
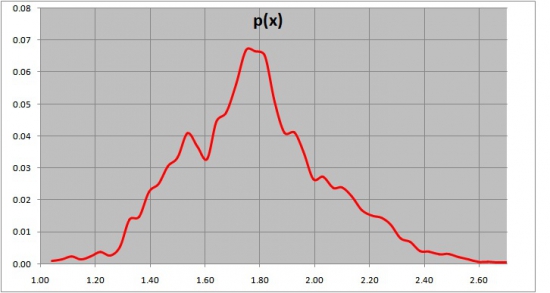
Понятное дело, что цена не меняется беспорядочно появляясь то там то тут между 1.1 и 2.7 как огни новогодней гирлянды, а имеет боле-менее упорядочные тренды, которые гоняют ее по диапазону, создающему уже такое вот распределение. Тем не менее, для нашего рассмотрения это приемлемое допущение. Действительно, функция плотности распределения цены означает вероятность нахождения цены в точке Х. Значит, мы можем считать, что, например, находясь в точке X рынок имеет отношение вероятности сдвинуться в точку X+d к вероятности сдвинуться в точку X-d (вырасти или упасть на d) такое же, как отношение плотностей вероятности p(X+d) к p(X-d). Это грубое допущение, но, по-моему, оно вполне приемлемо с практической точки зрения.
Далее, будем считать, что любую позицию, открытую на краях диапазона, закрывать всегда эффективней в его середине – по стат-нулю, считаемого в точке максимума распределения, как точке наибольшей вероятности.
Теперь легко посчитать функцию эффективности трейдов, как k(X)=p(X)|X-S|, где S – стат-ноль, которая будет иметь примерно следующий вид:
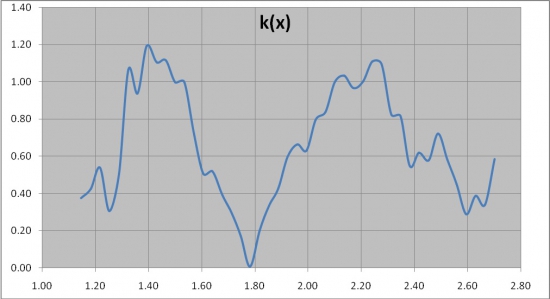
Получается, что сверху и снизу диапазона есть точки экстремумов – в нашем случае это 1.4 и 2.25, в которых совершение сделок наиболее эффективно. А именно, если рынок, например, падает от стат-нуля, равного 1.8, к нижней границе диапазона, то пока рынок выше чем 1.4 и функция эффективности растет, то все любые сделки заранее будут статистически проигрывать по эффективности потенциальным сделкам по ценам еще ниже. Таким образом, статистически выгоднее ждать дальнейшего падения рынка. И наоборот, если рынок падает ниже 1.4, то там функция эффективности уже падает, и ждать лучших цен будет уже статистически проигрышным делом. В итоге, самая эффективная стратегия будет заключаться в совершении одной сделки по 1.4 на весь потенциальный объем. Аналогично для верхней части диапазона, где лучшей точкой для сделки в нашем случае будет 2.25.
Вывод: для контр-трендовой торговли стохастического диапазона наиболее эффективным является торговля одной сделкой на весь объем в точках максимума функции эффективности вида ~p(X)|X-S|, где p(X) — функции плотности распределения цен диапазона X, а S – максимум p(X).
P.S. Проверено на практике.
Автор выражает признательность в помощи Шильникову Евгению.
...
По материалам http://vsemirnov.ru/

На каком тайм-фрейме – не принципиально. Она может быть как бесконечно устойчивой во времени, так и иметь локальный характер. Во втором случае арбитраж сводится к тому, чтобы нарезать в диапазонной торговле прибыли больше, чем потерять впоследствии на сдвиге диапазона или того хуже на трендовом выносе из него.
Так или иначе, пока стохастический диапазон держится, его можно контр-трендово работать.
Возникает вопрос об оптимальной стратегии такой контр-трендовой торговли.
Стандартный подход, используемый почти всеми арбитражерами, – пирамида сделок. Когда по мере отклонения от средней позиция наращивается с каким-то ценовым шагом. Обратное закрытие позиции может быть как таким же пошаговым, так и сразу всего объема в районе средней диапазона (назовем это статистическим нулем).
Смею утверждать, что это не самый оптимальный способ работы стохастического диапазона.
Представим весь диапазон в виде функции плотности распределения цены по ценовой шкале. Например, в случае вышепоказанного графика она будет иметь такой вид:

Понятное дело, что цена не меняется беспорядочно появляясь то там то тут между 1.1 и 2.7 как огни новогодней гирлянды, а имеет боле-менее упорядочные тренды, которые гоняют ее по диапазону, создающему уже такое вот распределение. Тем не менее, для нашего рассмотрения это приемлемое допущение. Действительно, функция плотности распределения цены означает вероятность нахождения цены в точке Х. Значит, мы можем считать, что, например, находясь в точке X рынок имеет отношение вероятности сдвинуться в точку X+d к вероятности сдвинуться в точку X-d (вырасти или упасть на d) такое же, как отношение плотностей вероятности p(X+d) к p(X-d). Это грубое допущение, но, по-моему, оно вполне приемлемо с практической точки зрения.
Далее, будем считать, что любую позицию, открытую на краях диапазона, закрывать всегда эффективней в его середине – по стат-нулю, считаемого в точке максимума распределения, как точке наибольшей вероятности.
Теперь легко посчитать функцию эффективности трейдов, как k(X)=p(X)|X-S|, где S – стат-ноль, которая будет иметь примерно следующий вид:

Получается, что сверху и снизу диапазона есть точки экстремумов – в нашем случае это 1.4 и 2.25, в которых совершение сделок наиболее эффективно. А именно, если рынок, например, падает от стат-нуля, равного 1.8, к нижней границе диапазона, то пока рынок выше чем 1.4 и функция эффективности растет, то все любые сделки заранее будут статистически проигрывать по эффективности потенциальным сделкам по ценам еще ниже. Таким образом, статистически выгоднее ждать дальнейшего падения рынка. И наоборот, если рынок падает ниже 1.4, то там функция эффективности уже падает, и ждать лучших цен будет уже статистически проигрышным делом. В итоге, самая эффективная стратегия будет заключаться в совершении одной сделки по 1.4 на весь потенциальный объем. Аналогично для верхней части диапазона, где лучшей точкой для сделки в нашем случае будет 2.25.
Вывод: для контр-трендовой торговли стохастического диапазона наиболее эффективным является торговля одной сделкой на весь объем в точках максимума функции эффективности вида ~p(X)|X-S|, где p(X) — функции плотности распределения цен диапазона X, а S – максимум p(X).
P.S. Проверено на практике.
Автор выражает признательность в помощи Шильникову Евгению.
...
По материалам http://vsemirnov.ru/
теги блога Всемирнов Алексей (Lemmy)
- CQG
- TOS
- Алексей Каленкович
- альфа
- анализ
- аналитики
- арбитраж
- аргумент
- баланс спроса и предложения
- бетта
- Блэк-Шоулз
- большинство
- будущее
- будущее мира
- бычья ловушка
- вебинар
- волновая теория Элиота
- голова и плечи
- голова-плечи
- графические формации
- двойная вершина
- демография
- Демура
- Евгения Случак
- золото
- зона поддержки
- импульс
- инвесторы
- индикатор
- инфляция
- инфляция в России
- конспирология
- конспирология теханализа
- коррекция
- кризис
- кукл
- кукловод
- купил и держи
- ловушка
- ловушки
- лонг-шорт
- математика рынка
- меньшинство
- МТС
- нефть
- нищеброды
- НОК
- он-лайн
- опционы
- открытие торговой сессии
- оффтоп
- парный трейдинг
- переоптимизация
- планшетник
- покупатели
- понедельник
- пресная вода
- прибыль
- продавцы
- проп
- проп-трейдинг
- прорыв
- работа
- разворот
- развороты
- распил бюджета
- риск-менеджер
- риски
- робот
- рынки
- сделки
- семинар
- сигнал
- смартфон
- смена тренда
- стопы
- тенденции
- теханализ
- технический анализ
- товары
- торговля
- торговый диапазон
- точка наименьших выплат
- трейдер
- тренд
- тренды
- улыбка волатильности
- уровень поддержки
- уровень сопротивления
- успешность
- успешный трейдер
- фильтр
- форекс
- футурология
- Хазин
- хедж-фонд
- Шевченко
- шип
- эмоции
- эффективность



















Мне думается тут какая-то ошибка… Ведь если мы считаем распределение стационарным, то очевидно, что вот эта функция эффективности должна расти монотонно и достигать максимума на краях.
Ведь если вы увидите, что в моменте отклонение максимально, а распределение не поменялось, то ведь если тут открыть трейд, а закрыть когда вернётся к нулевому отклонению, то тут-то и будет максимальный профит.
Пусть есть распределение цены p(x), которое считаем гаусовым с параметрами Mean=0, Sigma=S. Цена отклонилась на A и тут мы открыли позицию (купили или продали). Тогда результат открытой позиции будет иметь распределение также гаусово с параметрами Mean=A, Sigma=S. А поскольку сигма у всех позиций будет одинакова то среднее позиций растёт линейно с ростом отклонения X.
(правда тут я не считал, что мы закроем позицию в точке равновесия)
в модели в которой мы в любой точке X выбираем, что нам выгоднее — ждать роста X чтобы войти в более прибыльную сделку по Х+d или войти сейчас по X — в такой модели имеет смысл оперировать функцией пропорциональной X*p(X), которая имеет экстремумы на пути к краю диапазона
Кстати. У меня самого тактика похожая, но на 1 активе, не на спреде, и у меня распределения нестационарные…
Кстати 2. Может, вам будет интересно… Вот эта идея, арбитражная, применительно к 1 голому активу, статья у Давида Серебренникова:
Концепция многоуровневого маркет-мейкинга
y-dav.livejournal.com/8877.html
ну не в теме если, то че умничать? :-)
у меня это работает дольше, чем весь ваш опыт в рынке
эти подходы ток к арбитражу успешно применимы, в том числе статистическому