Я бы даже усилил это равенство — Инвестор должен быть Спекулянтом. Или даже так — Инвестор обязан быть Спекулянтом. Безусловно имеется в виду активный инвестор, постоянно управляющий своим портфелем, а не просто человек, купивший акции на 10 лет в надежде получать дивиденды и надеясь продать, если они вдруг вырастут.
Попробую объяснить. Однако, учитывая обилие постов, за последние 2 дня, о том как надо инвестировать и торговать — от весьма толковых до полной чуши, учить ничему не планирую.
Вначале банальные, но необходимые, истины. Инвестиции на рынке связаны с большими рисками. В России, при ее общем состоянии экономики, эти риски многократно больше.
Мы все читали про сверхуспешных Баффетов-Соресов и иже с ними. Возможно они владели неким инсайдом, но они что, заранее знали где дно? Допустим даже, знали. Они могли с их суммами закупиться одномоментно? — Нет, никак не могли — процесс затягивался минимум на месяцы.
В таком случае, каким же образом они сколотили или существенно преумножили свои состояния? Пахали сами и кормили штат сотрудников за 10-15% годовых? — Так это только немногим больше инфляции — особо не преумножишь.

( Читать дальше )

Да, да, самое время об этом подумать. На спокойном растущем или даже флетовом рынке в этом не было особой спешки, а вот сейчас это стало необходимостью.
В общем, меня вполне устраивал бы мой теперешний брокер — Альфа, я с ним с 2008 года. Если вы торгуете только акциями и фьючерсами, он и сейчас вполне ничего себе. Ну, не торгуй в периоды экстраактивности рынка, и не будет тебе никаких подвисаний.
У Альфа одна беда — они несколько лет назад исключили из своего меню торговлю опционами. Их нет как класса. Сейчас же опционы стали насущной необходимостью. Они стали необходимы уже в декабре, но это еще можно было пережить. В связи с последними событиями игнорировать отсутствие опционов в меню стало уже невозможно.
В общем, у меня была призрачная надежда, что Альфа вернет опционы, и я ждал. Сейчас уже ждать просто стало некогда, и надо подыскивать другого брокера 
Итак, начнем.

Оч.неплохой брокер IT-Invest.
Приемлемые тарифы для спекуляций фьючерсами-опционами.
Но для торговли акциями и инвестиций, если все это на одном счете, IT-Invest подходит плохо. Ведение депозитарного счета — 300 р/мес. Казалось бы, немного, но в год это уже 3600 р. При небольших месячных оборотах торговли акциями и примерно 5-10 сделках в месяц, а м.б., скажем, и всего 1-2 сделки, — это большие деньги. Совершенно непонятно с вводом-выводом средств ( у Альфы это делается в ЛК в течение минуты как перевод между своими счетами).

( Читать дальше )

Если честно, мне уже наплевать, что будет с рынком — я уже давно в кэше. Мне по фиг, что будет с Амерами и Европой — с ними все будет хорошо, если не замечательно.
У меня другая забота — что будет с рублем? И как это отразится на всех нас?
Я ещё не забыл предыдущие кризисы, когда вдруг оказывалось, что на зарплату можно купить всего несколько банок кофе. Интересно, что в 2008 г меня это меньше беспокоило. К чему бы это?

Я, в смысле инвестиций, вышел в кэш еще в декабре, о чем тогда же и позднее писал в комментариях, и пока куда либо входить не собираюсь. Когда рынок успокоится, немного начнет подрастать, тогда и начну входить. Частями — как принято. Но на падении и неясных перспективах не вижу никакого смысла.
Однако, смотрю, народ регулярно закупается — уж очень «вкусные цены», и на каждом падении продолжает наращивать портфели.
В связи с этим вспомнился старый анекдот, кажется он был в одной из книг Ф.Искандера.

Идут охотники по лесу, смотрят — большая нора. Стали обсуждать, чья это нора, и есть ли там какой зверь.
Один из охотников говорит — сейчас я посмотрю, и сунул голову в нору. И сидит там, головой в норе.
Его спрашивают — Ну, что там? Не отвечает.
Ждали, ждали, решили вытащить его из норы. Вытащили, смотрят — а головы то нет.
Стали спорить, а была ли вообще у него голова? Решили у жены спросить.
Принесли его домой, спрашивают у жены — Была ли у него голова?
Жена отвечает — Не знаю, была ли у него голова, но новую папаху он шил каждый год.

Эта, новость уже была на СЛ здесь, но, как выяснилось, мало кто обратил на нее внимания. Видимо, подвел заголовок темы — "Мосбиржа анонсировала изменения на срочном рынке".
Исходная новость от МОЕХ здесь - https://www.moex.com/n26656/?nt=107

Но, самое интересное в новостях от ARQA по этому поводу -  https://forum.quik.ru/forum1/topic5117/   Все текущие версии QUIK перестают полноценно работать на срочном рынке. Не обольщайтесь, в рамках дальнейшей модификации и фондовый рынок постигнет та же участь.) Придут и за вами.)
Ну, и самое главное, хорошая шутка от ARQA — «Для   решения проблем пп. 5-6 следует установить версию терминала QUIK,  которая на момент публикации данного уведомления еще не вышла, но  планируется к выпуску до того, как данное изменение в торговой системе  будет внедрено.»

Если подвисает сам брокер или связь с ним, то этот топик вам не поможет.
Однако, возможно  причина и в самом терминале Quik. Дело может быть в том, что Quik в процессе работы пишет данные в файлы вида *.dat и *.log, и со временем эти файлы сильно разрастаются и запись в них данных занимает значительное время, отнимая процессорное время у других задач.
Простейший выход из этого состояния — периодическое удаление файлов *.dat и *.log из директории Quik. Для этого надо написать небольшой командный файл всего в одну строчку, разместить его в директории Quik, где находятся удаляемые файлы, и, для удобства использования создать ярлык на рабочем столе.
Итак, открываем блокнот и создаем файл Quik_start.cmd В него помещаем всего одну строчку: 

del alltrade.dat curr_data.log info.log
 

После команды не забудьте нажать Enter, чтобы последней в файле была пустая строка.
Сохраняем файл в указанной выше директории (папке), создаем ярлык и переносим его на рабочий стол. Запускаем командный файл перед стартом Quik. При этом файлы, указанные в команде del будут удалены. При запуске Quik их создаст заново.

( Читать дальше )

Посмотрите на тематику сайта последние 2-3 недели — коронавирус, кризис — уже наступил, или еще только собирается, покупать или продавать, обсуждение падения, от все пропала до мы еще о-го-го, и счас как отскочим в небеса.
До каких-то Lua, DLL и автоторговли сейчас нет никому никакого дела. Кто сейчас это будет читать, когда и в более спокойные времена читали лишь немногие. Писать просто так не хочется, писать для себя — мне это тоже не нужно.
В общем, решил подождать с этой темой до лучших, более спокойных, времен. А там посмотрим, м.б. высохнет, и само отвалится.

Смотрим сюда


44 подписчика.
А теперь сюда.


( Читать дальше )

Эти дискуссии с завидной регулярностью появляются на форуме. Из них следует, что трейдеры это такие уникальные существа, приобщенные к тайным знаниям, и далеко не каждый на это способен. Ну, и доказательство, вот оно — 95% теряют депозиты. 5% — избранных богом. Хочется снять шляпу и преклонить колени.
Но вначале давайте об инвесторах — каждый ли может стать?
Инвестор на рынке- это долгосрочные вложения в какие-либо активы с целью получения прибыли. Обычно прибыль в %% не очень значительна. Обычно это портфель, состоящий из нескольких активов.
Понятно, что для инвестиций уже нужна большая свободная сумма денег, и не у каждого таковая найдется. Со 100-200 тыс р. заниматься инвестициями не имеет особого смысла. Можно конечно наугад взять несколько активов, которые, вроде, должны расти, особо не заморачиваться, и считать себя инвестором. Ну, да, в принципе, можно.
Но с большими суммами номер уже не прокатит — этими деньгами надо постоянно заниматься. Всякие фундаментальные, политические, экономические, корпоративные и технические факторы — во всем этом надо хорошо ориентироваться и неплохо разбираться, все это надо учитывать. Надо постоянно отслеживать портфель, что-то в него включать, что-то исключать, оценивать и переоценивать — что уже можно продать с прибылью или убытком, а что подождать.Все перечисленное взаимосвязано.

( Читать дальше )

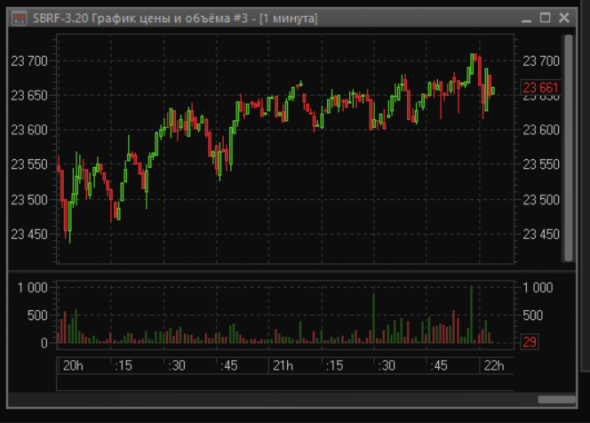
Это я здесь еще индикаторы не нарисовал, а то бы выглядело все как по нотам. Сиди, и только дел -открылся — закрылся, и 50-70 п твои. Даже думать не надо.