Избранное трейдера CkPyDG
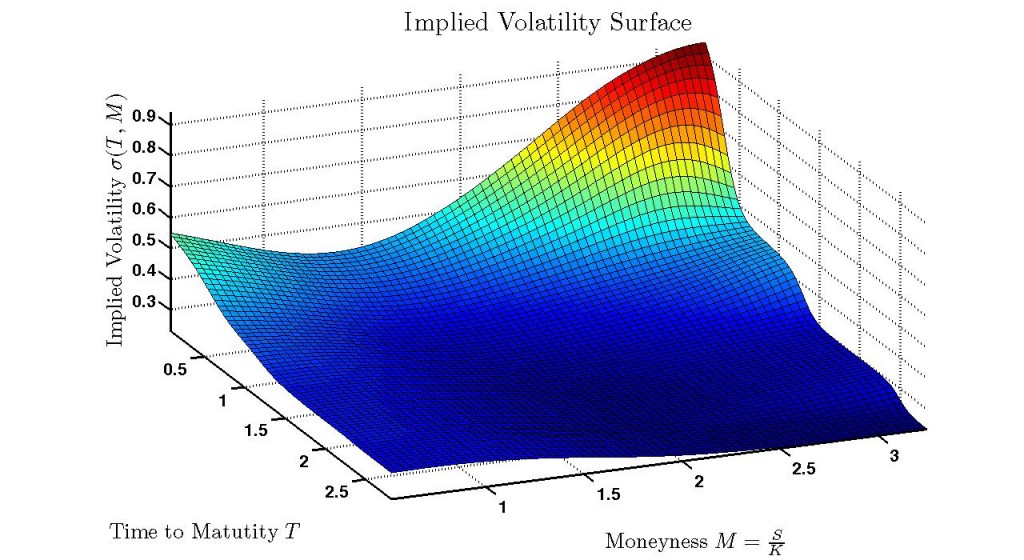
Улыбка волатильности. Ad-hoc Блэк Шоулз
- 29 апреля 2015, 10:29
- |
В ряду алгоритмов, используемых в опционной торговле, значительное место занимают стратегии покупки/продажи волатильности. Смысл таких стратегий в покупке опциона, когда волатильность рынка мала, и соответственно, продаже, когда волатильность высока, при постоянном хэджировании базисным активом ( дельта позиции равна нулю).
Цена опционов, как известно, вычисляется по формуле Блэка-Шоулза, однако из-за того, что некоторые допущения, относящиеся к модели цены базисного актива, не соответствуют реальному статистическому распределению, опционам разных страйков приходится присваивать различные значения так называемой подразумеваемой волатильности (IV), которая входит в уравнение Блэка-Шоулза как параметр. Возникает ситуация с двумя неизвестными — мы вычисляем IV по текущей цене опциона, при этом не зная, насколько справедлива эта цена в настоящий момент, следовательно не можем определить, дешево стоит опцион сейчас или дорого. Если бы нам удалось определить истинную волатильность рынка, то рассчитав по ней цену и сравнив с текущей, можно было бы принимать решение о покупке или продаже опциона. Поэтому основная задача, которую нужно решить в стратегиях покупки/продажи волатильности — построение правильного графика подразумеваемой волатильности опционов, в зависимости от страйков, из-за его формы имеющим название улыбки волатильности, или поверхности волатильности, если речь идет о разных периодах до экспирации — см. график в заглавии.
( Читать дальше )
- комментировать
- ★20
- Комментарии ( 17 )
В 2015г. Правительство РФ ставит в приоритет ОПК
- 28 апреля 2015, 09:16
- |
Разбираем ОАК (iАвиастК ао):
- В начале 2015г. В корпорации была смена руководства. На пост Президента ОАК назначен Слюсарь Ю.Б., который ранее был зам.министра промышленности и торговли Российской Федерации. Это говорит о том, что продвижение продукции ОАК на мировые рынки сейчас идет на уровне Государственных интересов.
- На 2015г. в ОАК запланирован выпуск продукции на 20% больше чем в 2014г., а так же прирост валовой выручки с 285 млрд. рублей до 400 млрд. рублей.
- Рыночная капитализация корпорации сейчас составляет порядка 45млрд. рублей! Цена акций 25коп., при номинале 86коп. Капитализация всей авиаотрасли России получается мусорная. А по данным последнего баланса активы АвиастК ао составляли 334 млрд.р. – эти можно посмотреть на сайте ОАК, они есть в свободном доступе.
( Читать дальше )
Московская биржа объявляет о проведении конкурса "Я - Инвестор"
- 28 апреля 2015, 08:06
- |
Московская биржа проведет летом 2015 года конкурс «Я — Инвестор», который пройдет на игровом сервере биржи в условиях, максимально близких к реальным торгам.
Участникам соревнования могут стать физические лица, открывшие брокерский счет на любом из рынков не ранее 1 июля 2014 года и делающие первые шаги на биржевом рынке.
В течение двух месяцев участники смогут заключать сделки с 20 акциями и ETF, семью фьючерсными контрактами и четырьмя иностранными валютами, и таким образом смогут получить реальные навыки торговли без риска потерять собственные деньги.
Призовой фонд конкурса составит 8 млн рублей. Победителями станут участники, получившие в результате своих операций на игровых торгах положительный результат.
Регистрация участников начнется с мая 2015 года и будет проводиться брокерскими компаниями, список которых будет размещен на сайте конкурса.
Дополнительная информация о конкурсе (время и порядок проведения, порядок определения и награждения победителей) будет раскрыта на сайте конкурса в ближайшее время.
moex.com/n9315/?nt=106
Альтернативный расчет стоимости опционов 2. Формула сферического опциона в вакууме
- 24 апреля 2015, 12:06
- |
В прошлых статьях (smart-lab.ru/blog/248456.php, smart-lab.ru/blog/250544.php ). Я пытался написать альтернативную формулу для расчета цен опционов. Но взятая из существующего научного арсенала формула, для проверки гипотезы оказалась не совсем корректна, и даже после подгонки как-то не внушала доверия. Поэтому пришлось делать всё самому с самого начала и придумать свою теорию «распространения взаимодействия», на основе которой и рассчитывать цены опционов.
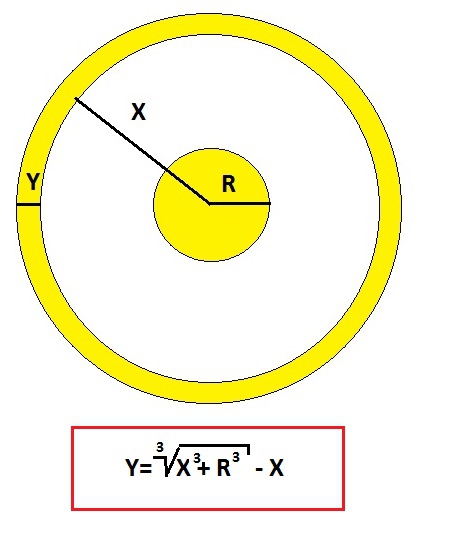
И так, возьмем, к примеру гравитацию (потому как, никто не знает что это такое, а следовательно придирок к мелочам будет меньше). Пусть у нас есть некая точка, оказывающая на окружающий мир гравитационное воздействие. Представим это воздействие а виде шара радиусом R, где сила воздействия равна R. ( для опционов это W – цена опциона на деньгах):
Теперь представим, что шар начинает расширятся, с образованием в центре пустоты, и превращается в некую сферу. Общая сила воздействия (энергия заключенная в R ) остается постоянной. И объем начального шара равен объему оболочки сферы толщиной
( Читать дальше )
Посты Атамана и Нео
- 24 апреля 2015, 09:03
- |
Время от времени эти посты кто то выкладывает, некоторые платно.
Старая тема на смартлабе: smart-lab.ru/blog/136886.php там их фоты и полно интересной инфы.
Для фанатов трейдинга которые ещё не знают.
Посты (Конспекты.rar, вверху стрелочка скачать) drive.google.com/file/d/0BzrzVQF_vqJDYUxXRGhFenppWVU/view?usp=sharing
Альтернативный расчет стоимости опционов.
- 21 апреля 2015, 21:48
- |
В прошлый раз мы определили стоимость опциона на деньгах. smart-lab.ru/blog/248456.php Теперь попробуем рассчитать стоимость опциона вне денег. За базу отсчета возьмем полученную ранее цену опциона на деньгах и обозначим ее буквой W. Это вроде как, некий параметр включающий в себя вегу и тэту (для любителей стандартного представления).
Теперь, посмотрим на изменение цены базового актива немного под другим углом. Представим, что потенциальная возможность изменения цены из точки, в которой она находится сейчас в другую точку, (волатильность) есть некая мощность излучения заложенная в данной точке. То есть, волатильность мы представим как мощность излучателя возмущений некоего «финансового пространства».
И цену опциона на деньгах, мы можем представить как результат воздействия этого «излучателя» на опционное пространство данной серии опционов в нулевой точке ( в эпицентре).
То есть W (цена на центральном страйке) – это мощность источника излучения «волатильности» в опционном пространстве. А цены на страйках вне денег – это значения мощности сигнала на расстоянии от источника излучения. И чем дальше страйк, тем слабее сигнал.
( Читать дальше )
По заказу благодарных зрителей выкладываю презентацию своего выступления на конференции смарта 18.04
- 18 апреля 2015, 18:53
- |

http://www.files.co.uk/shared/5531e95db55f8/%D0%92%D1%8B%D1%81%D1%82%D1%83%D0%BF%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5%21.zip
Мои контакты :
tel./viber/whatsapp/theema: +447700041782
e-mail: sf.bankir@aol.co.uk
========
Портал о банковской отчетности "Куап.ру" посвящен анализу банков.
Целевой аудиторией портала являются банковские и финансовые аналитики, а также журналисты, пишущие на финансовые темы. Портал содержит:
— приведенную к удобному для пользователя виду информацию по ключевым показателям банков России и ряда стран СНГ — балансовые показатели, прибыль, обязательные нормативы, капитал, число точек продаж, региональное присутствие;
— рассчитанные основные производные показатели — доходность активов и капитала, операционная эффективность, доля просрочки и норма резервирования;
— возможность сравнения банков между собой;
— возможность сложения нескольких банков и просмотра агрегированных показателей;
— гибко настраиваемую систему ранжирования банков по различным показателям;
— аналитические материалы по российской банковской системе.
( Читать дальше )
Правительство обложило доходы физлиц от продажи валюты подоходным налогом!
- 13 апреля 2015, 22:21
- |
Нервотрепка на валютном рынке, начавшаяся в конце минувшего года, докатилась до налогоплательщиков. Правительство решило обложить доходы физлиц от продажи валюты подоходным налогом. Тех, кто не внесет до конца апреля прибыль в налоговые декларации, ждут пени и штрафы. Правда, нововведения коснутся только тех граждан, кто имел несчастье легально продать крупную сумму евро и долларов.
Короче, если вы законопослушный гражданин и в 2014 г. имели удовольствие или несчастье легально продать (именно продать, а не купить) валюту на сумму свыше 250 тыс. рублей в эквиваленте (включая эпизоды, когда часть средств с валютной пластиковой карты вы снимали в рублях или поручали банку реализовать вашу безналичную валюту для погашения кредита/процентов), поспешите до конца апреля подать налоговую декларацию и уплатить соответствующий налог. Иначе — штрафы, пени и нервотрепка. К тому же программа для составления декларации есть на сайте ФНС и предлагается к скачиванию (вы не поверите!) абсолютно бесплатно.
Полная информация тут
10 чисел, на которых держится мир
- 12 апреля 2015, 08:23
- |
Чтобы создать Вселенную, даже небольшую, нужны числа, без которых она просто не запустится. Это — фундаментальные константы. С помощью этих десяти чисел можно описать все: и рост снежинок, и взрыв гранаты, и игру на бирже, и движение галактик. А вот откуда они взялись — непонятно. Желающие могут списать их появление на божью волю. А воинствующим атеистам остается только ими пользоваться, объясняя с их помощью как ход эволюции, так и температуру Благодатного огня...
Пространство
Число Архимеда
Чему равно: 3,1415926535… На сегодня просчитано до 1,24 трлн знаков после запятой
Кто и когда открыл:
Точное авторство неизвестно. Приписывается древним индусам, грекам, китайцам и прочим хорошим людям. Впервые обозначил его греческой буквой π в начале XVIII века английский математик Уильям Джонс( Читать дальше )
Вокруг одни пузыри - куда в долгосрок?
- 09 апреля 2015, 21:38
- |
Озадачился тут, куда разложить новые накопления и какие классы активов привлекательны для инвестирования на 1+ год и пришел к неутешительным выводам. Откинем многочисленных стар-трейдеров, которые тут генерят по 100% в год — мы люди недалекие и скромные, поэтому главная задача — не пропинать нажитое непосильным трудом. Вот какие идеи я рассмотрел:
- Российские корпоративные евробонды — неплохо отработали, на мой взгляд лучшая идея последних месяцев, которую я успешно реализовал, но сейчас уже для долгосрока не так привлекательны — прилично отросли, многие компании уже осуществили байбеки и апсайд уже невелик
- Российский акции — не годятся из-за низкой ликвидности (в глобальных масштабах это песочница), высокой волатильности и непрозрачности (инсайдер сидит на инсайдере и инсайдером погоняет) — потолок высокий, но пол стеклянный
- S&P — растет как на дрожжах уже слишком долго плюс крепчающий доллар и спекуляции о повышении ставок, которые были нулевыми слишком долго, чтобы это прошло безболезненно — есть ощущение, что Олейник может наконец-то оказаться правым и коррекция не за горами. С другой стороны, фундаментально рынок очень хорош, да и растет довольно бодро. Вывод: хрен его знает, возможно остановлюсь на секторальной аллокации (другая тема)
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал