Слился полностью, закрыл позиции, осталось денег на полтора контракта RIZ.
Налицо полное неумение торговать. Необходимо пересмотреть все принципы торговли.
Хоть и тяжело, но полностью сдаться и пойти работать мешает портфель акций, хотя и они абсолютно все в минусах двухзначных. Хорошо хоть на ММВБ без плеч. Хорошо, что без единого кредита. Но наверное это плохо, лучше бы если у меня ничего не осталось.
Наказать себя как то надо.  Хочу морить себя голодом, хватит ли на это силы воли? Буду жить только на хлебе и воде начиная с сегодня на месяц до 1 декабря, кусок хлеба на завтрак, два куска хлеба на обед, кусок хлеба на ужин. Кроме этого каждый день буду мучить тело бегом по 10 км в день. Если сорвусь хотя бы раз, то пойду работать, если не сорвусь и продержусь до 1 декабря, то подумаю как дальше быть.

Налоговый кодекс вводит новый вид налогового вычета – инвестиционный. Что это за вычет, в каком случае его можно получить? Я хочу сегодня рассказать о нем.
Новый вид вычета связан в первую очередь с новым понятием «инвестиционным счетом».
Что такое «инвестиционный счет»? Инвестиционный счет – это счет внутреннего учета. Он предназначен для обособленного учета денежных средств, ценных бумаг физического лица (клиента), обязательств по договорам, которые заключены за счет клиента.
Чем отличается новый инвестиционный счет от брокерского?
Инвестиционный счет отличается от брокерского счета тем, что по инвестиционному счету предусматривается два вида налоговых вычета.


( Читать дальше )

Продолжение цикла статей про исследование стратегии, покупка стрэдла.
Перед тем как улучшать нашу систему посмотрим на временные характеристики опциона. Для начинающих опционщиков думаю будет полезно.
Для этого я взял сентябрьский квартальный опцион (можно было любой другой взять, смысл не изменится). Так как в данный момент нас интересуют временные характеристики, то соответственно волатильность и цена не должны меняться. Просто скопируем волотильность и цену фьючерса взятую с первого дня опциона на весь период жизни опциона. Посмотрим чего получилось, в дальнейшем все расчеты для одного опциона на индекс РТС.

1. Премия опциона.
 
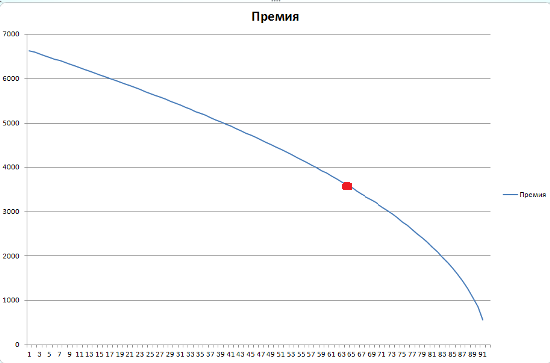
Видно, что премия опциона потихоньку уменьшается со временем. Причем чем ближе к экспирации тем быстрее премия уменьшается. Точкой я отметил, где премия цены опциона теряет половину, это гдето 64 день. Получается, что опцион теряет половину своей цены примерно за 70% своей жизни и в остальных 30% своей жизни теряет остальную половину. Это так для общего развития, на самом деле меня интересуют другие три товарища, это тетта, гамма и вега, по другому греки.

( Читать дальше )

В продолжение: smart-lab.ru/blog/tradesignals/206807.php
Купил на 10 % от депозита колов декабрь 120 страйк по 1340 пунктов.
Будем на уровне 104 000 добавлю 115 и 120 страйк на 15 % от депо.
Цель собрать букет колов до разворота тенденции, защита будет только от 95 000 пунктов по Ри.
Всем профита и успехов!

Приводов для быстрого ввода заявок так много, что времени нет для их рассмотрения.
Несть числа им, да и обзоров море:
1. smart-lab:  Статья: анализ скальперских приводов
2. smart-lab:  Супер список приводов для торговли на бирже!!!
3. 2stocks  :  На выбор скальперу — обзор 14 приводов
4. quik        :  Полезные ссылки
А вот простого, как «три аккорда», незатейливого — не было.
Теперь он есть:


1. написан на LUA, с исходным кодом, приправлен комментариями;
2. бесплатен, без ограничения сроков, «Free software».
3. без графики и хоткеев всяких.
Настройки — в строках кода:

• account = 'SPBFUT00R86' — код торгового счета
• classCode = 'SPBFUT' — код класса
• secCode = 'SRZ4' — код бумаги
• WorkSize = 10 — рабочий размер
• OpenSlippage = 50 — проскальзывание
• FREQUENCY = 500 — частота привода (в миллисекундах)

Скачать: SuperScalp.lua
UPD 04.10.2014г. Привод написан для FORTS.
 
 
 

Палю свой фибо грааль на вебинаре «Голос рынка» — День открытых дверей, гость Анатолий Демонов. Смотрим, присоединяемся, комментируем! Гусятничество не приветствуется!

Я обещал написать про индекс волатильности. Последний раз я серьезно занимался виксом давно, а именно летом 2011 года, когда его только запускали. Поэтому сейчас пришлось вспоминать свои старые мысли. Иногда это бывает полезно, но, к сожалению, в этот раз новые мысли не последовали за старыми.

Итак, приведенные размышления очень наглядно покажут, что такое викс. Запишем изменение цены опциона в виде

dO = delta * dS + 0.5 * gamma * dS^2 + theta * dt + vega * dSigma +…, (1)

где, разумеется, греки зависят от (S, K, T, sigma). Теперь представим себе, что  дельта и вега портфеля нейтральны и забудем про них, а займемся членом

dO' =  0.5 * gamma * dS^2 + theta * dt, (2)

вечной борьбой льда и пламени (теттой и гаммой). Посчитаем, что процесс у нас броуновский (хотя бы локально), то есть

dS^2 = S^2 * sigma_m^2 * dt. (3)

Я специально ввел обозначение sigma_m, чтобы подчеркнуть, что речь идет о волатильности БА. Далее подставим (3) и формулы отсюда http://en.wikipedia.org/wiki/Black–Scholes для тетты и гаммы в (2) и получим

( Читать дальше )

Вернувшись в конце июня из отпуска с семьей, встал вопрос – участвовать ли в июльской экспирации. До нее оставалось всего 2 недели и ранее к этому сроку я обычно выходил со сформированной позицией. Я готов был принять небольшой убыток или хорошую прибыль и уже не предпринимал никаких активных действий по управлению. Все в большей степени зависело от рынка. В июне получился довольно неплохой результат +33% на планового ГО, которое благополучно увеличилось вслед за движением рынка.
В этот раз было принято решение строить стратегию от продажи волатильности. Был выделен 1 млн. рублей под ГО. Продажу решил начать с центральных страйков и по мере движения рынка покрывать новые диапазоны (считаю эту технику более прибыльной в отличие от дельта-хеджирования). Одновременно с этим была куплена страховка в виде спрэдов на случай сильного движения цены в ту или иную сторону. Всего в результате управления было проведено 5 итераций, задействовано 5 страйков.
В итоге позиция на экспирацию оказалась следующая (зеленая линия – конечный профиль)


( Читать дальше )

Если Вы занимаетесь частыми внутридневными сделками и/или скальпируете через терминал Quik, то вопрос о подходящем и удобном для Вас приводе встал наверно после того, как Вы совершили первую сделку в Квике?))))

Сейчас, я остановился на единственном удобном приводе QScalp Николая Морошкина! Сейчас уже доступна версия 3.4.
moroshkin.com/qscalp.html
Обсуждение, поддержка, ответы на вопросы:
www.2stocks.ru/forum/index.php?showtopic=15501&view=getlastpost

Кстати, QScalp наиболее удобная и подходящая для скальпинга программа из всех доступных, после QuikOrdersDOM это как Небо и Земля!


QScalp- тот же аналог «привода Бондаря», но под Quik. Также, доступен и исходник, написанный на C#.

( Читать дальше )

Добрый день!
Для того чтобы настроить скальперский стакан в квике необходимо следовать инструкциям в руководстве по эксплуатации http://www.quik.ru/depot/quikref.rar документ №5, глава 5.7.9.
Для Вашего удобства взял от туда вырезку, кому качать не охота.
5.7.9       Режим «Быстрый ввод заявки»
Если в настройках Таблицы котировок установлен флажок «Быстрый ввод/снятие заявки», то включается режим быстрого ввода заявок, который предусматривает ввод и снятие заявок в стакане котировок с помощью кнопок мыши. Данный режим требует включения панели инструментов в Таблице котировок.
Параметры заявки «Торговый счет», «Код клиента», «Примечание» заполняются значениями из полей «А», «С» и «М» на панели инструментов Окна котировок. Данные поля должны быть видимыми на панели. Если поля «С» и «М» не отображаются на панели, то параметры «Код клиента» и «Примечание» в заявке не будут заполнены.


( Читать дальше )